Рычажные механизмы: анализ, типы, применение

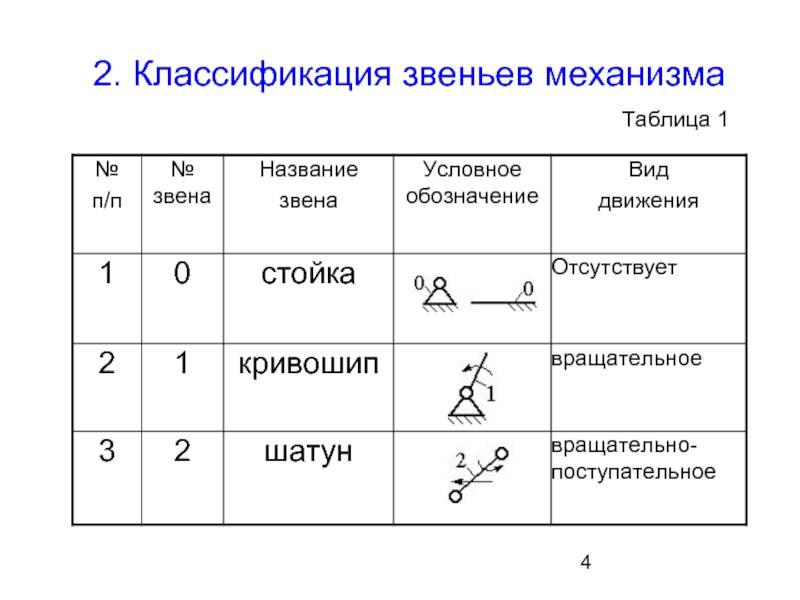
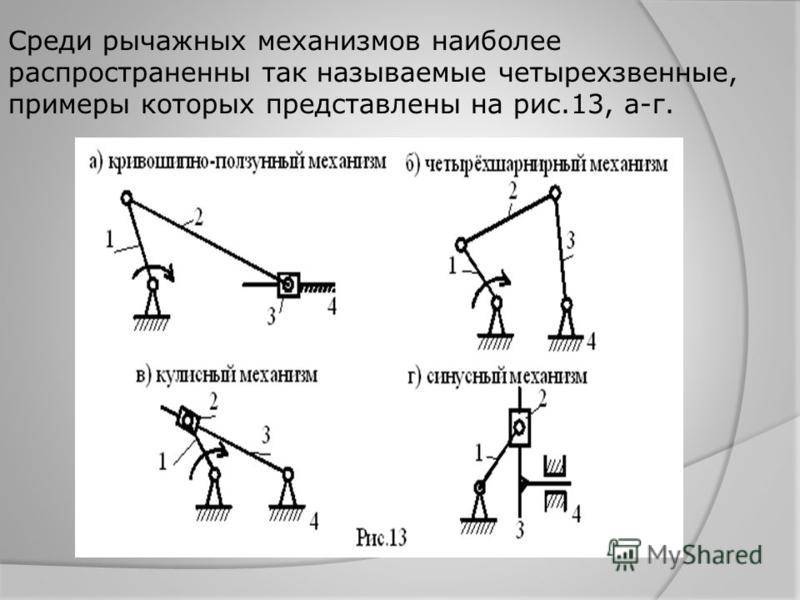
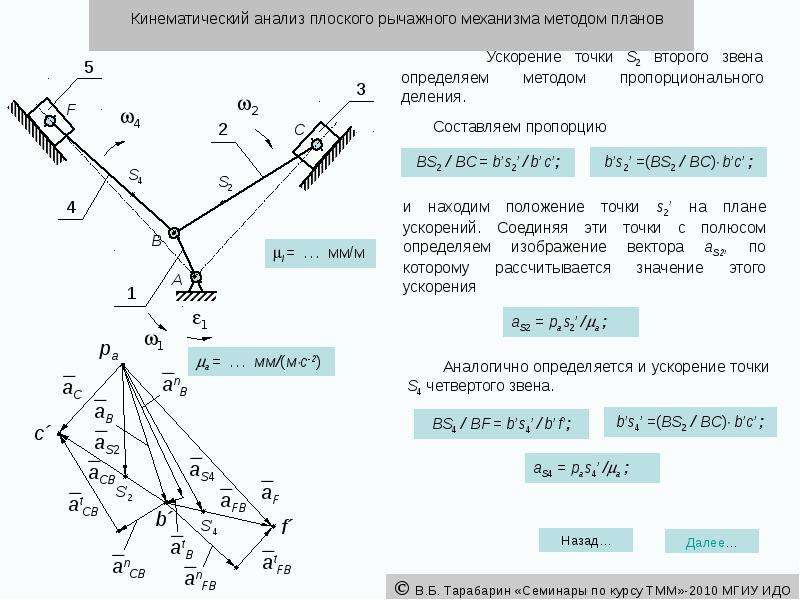
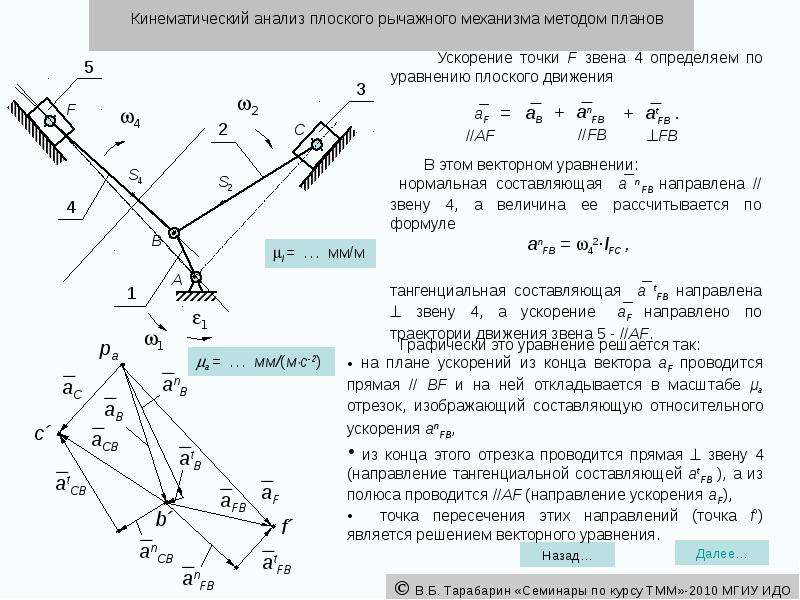
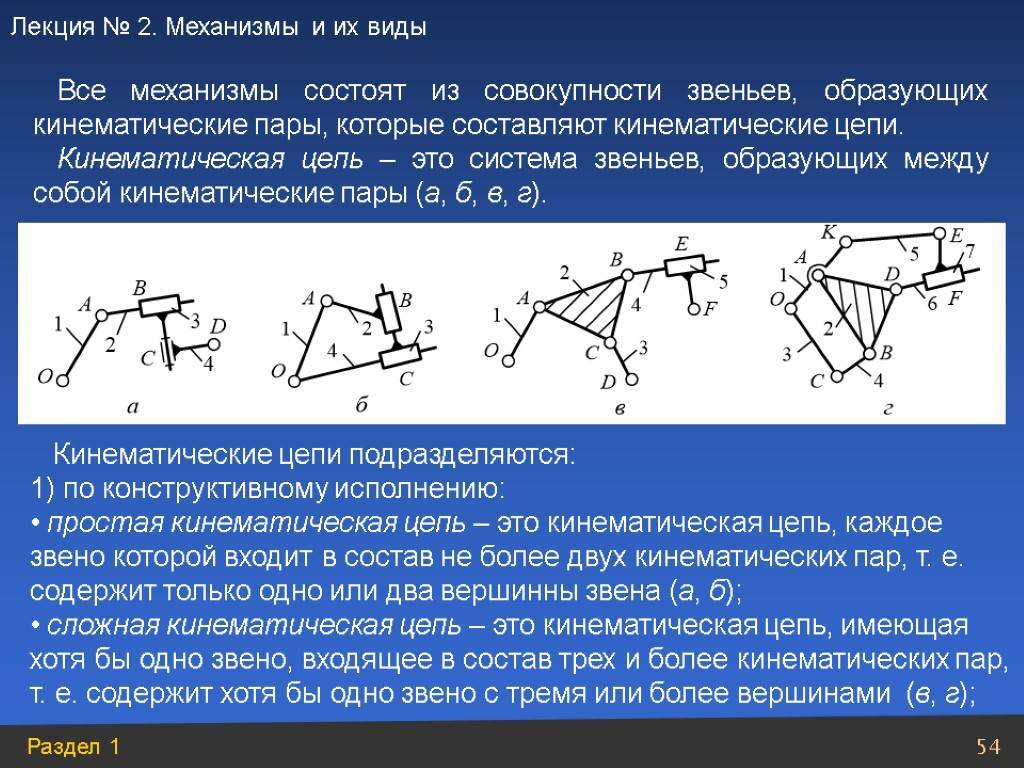
Структурный анализ рычажных механизмов

Проводя исследование рычажного механизма следует уделять внимание возможности выбора двух основных направлений, одно из которых связано с непосредственным анализом, другой синтезом. Оба понятия существенно отличаются друг от друга, что нужно учитывать. Структурный анализ – процесс определения структурных особенностей, который может заключаться в следующем:

Структурный анализ – процесс определения структурных особенностей, который может заключаться в следующем:

1. Определении кинематической пары.
2. Изучение структур групп.
3. Определение особенностей связи кинематической цепи.

Сегодня анализ проводится для определения дефектов структуры, которые в дальнейшем при необходимости могут устраняться.

Каждый случай исследования по-своему уникален

В рассматриваемом случае уделим внимание плоскому рычажному механизму, характеризующийся нерациональной структурой. Его особенности заключаются в нижеприведенных моментах:

1. Работоспособность механизма сохраняется исключительно при определенном соотношении длины звеньев. Образующаяся фигура в ходе построения напоминает параллелограмм.
2. Для исключения вероятности эксплуатации устройства с дефектами следует точно знать о наличии или отсутствии избыточных взаимосвязях, возможности пассивного распространения и их количества. Стоит учитывать, что они могут возникать исключительно в кинематических цепях замкнутого контура.
3. На сегодняшний день выделяют два основных типа контуров: замкнутые и зависимые. Независимым считается вариант исполнения, у которого хотя бы один элемент контура отличается от других.

Зависимые варианты исполнения дублируют друг друга. Для определения числа контура применяется специальная формула.

Также для исключения вероятности появления дефекта проводится расчет количества структурных групп и некоторые другие моменты. В общем можно сказать, что проводимый анализ направлен на достижение следующих задач:

1. Построение различных механизмов. При этом проводится определение подвижности и маневренности, так как подобные параметры считаются основными.
2. Создание плоских механизмов. Процедура подразумевает анализ состава структуры, а также определяет подвижности.

В целом можно сказать, что преследуемые цели зачастую направлены на определение возможной деформации структуры. Провести полноценный анализ можно только при всестороннем рассмотрении механизма.

Что происходит после нажатия рычага/кнопки?

Изначально активируется шток, производящий подъем пробковой груши – запорного клапана сливного узла, в результате чего вода из накопительной емкости свободно проникает в унитаз, омывая его рабочую поверхность, после чего попадает в канализацию. Потом пробка под воздействием собственной массы становится на место. перекрывая ток воды в унитаз.

Одновременно с падением уровня воды в резервуаре открывается запорный клапан впускного механизма и осуществляется наполнение бачка рабочей жидкостью. Этот процесс прекращается по достижении поплавком верхнего положения, которое обычно устанавливается на 20-30 миллиметров ниже боковых отверстий резервуара.

Основные параметры кулачкового механизма

Наиболее важными параметрами устройства, определяющими его рабочие качества, служат:

• наибольший ход толкателя (ход плеча коромысла);
• наибольшая скорость поступательного перемещения;
• траектория исполнительного органа.

Кроме того, в расчете участвуют и такие характеристики, как:

• скорость вращения приводного вала;
• заданное усилие на исполнительном органе;
• период работы, у большинства схем принимается равным полному обороту вала (2π);
• фазовыми углами Θ

Фазовые углы различаются на следующие:

• фаза удаления Θу – угол, при повороте вала на который происходит максимальное перемещение толкателя между его крайними положениями;
• фаза верхнего стояния Θв.в- угол максимального удаления толкателя от оси кулачка;
• фаза сближения Θс соответствует перемещению толкателя из дальнего в ближнее положение, противоположна по смыслу фазе удаления, но не обязательно равна ей по величине;
• фаза нижнего стояния Θ н.в — соответствует минимальному удалению и по смыслу противоположна Θ в.в.

Если сложить все фазовые углы, должна получиться полная окружность

Θ = Θу + Θв.в + Θс + Θн.в =2π.

Рабочий ход складывается из первых трех фаз:

Θр.х= Θy+ Θв.в+ Θс.

Холостой ход образуется из фазы нижнего стояния:

Θх.х= Θн.в.

Каждой фазе работы ставится в соответствие один из профильных углов Σ: Σу; Σв.в; Σс; Σн.в.

Обычно фазовый и профильный угол для каждого состояния не равны между собой

Θ ≠ Σ.

Расчет кинематики кулачкового устройства базируется на линейных и угловых размерах его компонентов. Соотношение между ними называют законом выходного звена кинематической схемы.

Его выражают как функцию от текущего угла поворота вала, он учитывает все свойства структуры системы и ее проектных характеристик:

S =f(Θ), где Θ – угол поворота ведущего вала.

Закон выходного звена можно получить двумя методами:

• расчетно-аналитическим;
• графоаналитическим.

Расчетно-аналитический способ существенно более точен, но требует сложных расчетов. Его используют как основной при проектировании ответственных механизмов.

Графоаналитический способ вычисления закона проще в исполнении и значительно более нагляден. Его используют для простых устройств и как способ предварительной оценки пред проведением расчетно- аналитических вычислений.

С развитием средств вычислительной техники и программного обеспечения сложности расчетно- аналитического метода отошли в прошлое. Средства трехмерного параметрического моделирования и кинематической симуляции, предлагаемые всеми ведущими производителями программных продуктов семейства CAD- CAE, позволяют одновременно проводить графическое моделирование и аналитические расчеты, существенно облегчая работу конструктора.

Классический графоаналитический способ реализуется:

• построением кинематических диаграмм;
• формированием кинематических планов с применением заменяющего механизма.

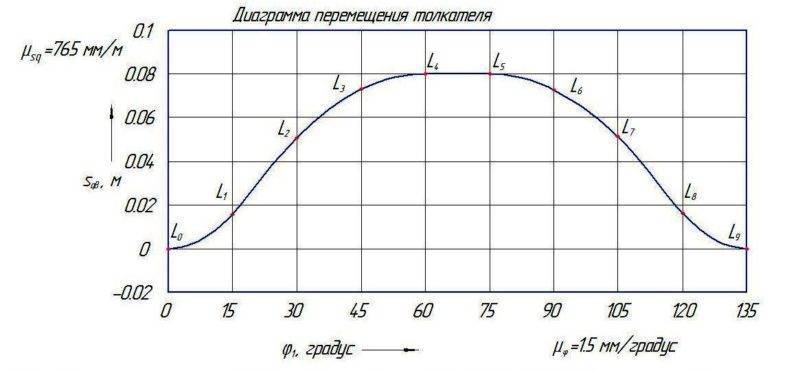
Чертеж его представляет собой упрощенную модель, содержащую лишь низшие пары. Их отличительное свойство заключается в том, что они обладают в фиксированных положениях ведущего звена теми же значениями координат, скорости и ускорения, как и у моделируемых ими компонентов высшей пары.

Во время построения упрощенной модели следует следить за тем, чтобы сохранялись законы движения ведущего и ведомого элементов кулачкового устройства, а также относительное положение их осей.

Пара высшего порядка моделируется связанной двойкой низших пар. Вследствие этого в схеме возникает фиктивное третье звено, а вместо схемы кулачковых механизмов подставляют эквивалентную схему рычажной системы.

Обычно функция движения выходного звена имеет вид второй производной расстояния по углу положения вала либо по времени. Тогда она имеет физический смысл ускорения, и для графического моделирования применяют способ построения кинематических диаграмм.

Цилиндровые замки с фалевой защелкой

Врезной замок с защелкой функционален, удобен в использовании.

Цилиндровые замки с фалевыми защелками закрываются под механическим воздействием. Она является вспомогательным элементом запорного механизма. Фалевая защелка бывает с фиксатором язычка и без него, с одной или двумя ручками. Такие замки часто используют в жилых и производственных помещениях.

Фалевые ручки используют для входных и межкомнатных дверей. В ней нет никакой функциональной особенности, это скорей элемент декора. Удобство в том, что при изменении интерьера, чтобы замыкающее устройство вписалось в образ – достаточно подобрать ручку по стилю.

Ручки для входных дверей устойчивы к внешним воздействиям, выполнены из прочных материалов (если сравнивать с межкомнатными).

По типу нажатия ручки бывают:

• Нажимные (для входных дверей).
• Поворотные (для межкомнатных дверей).

Нажимная ручка тоже подойдёт для межкомнатных конструкций. Выбор зависит от предпочтений покупателя.

4.3 Расчёт параметров зубчатых колёс

Рассчитываем смещение колёс

Так как , то

Так как , то

Коэффициент суммы смещений

                                               (4.15)

где,  – смещение 1-го колеса

 – смещение 2-го колеса

Определим угол зацепления по формуле

                                        (4.16)

где, ,  – эвольвентная функция углов  и

Межосевое расстояние определим по формуле

                                (4.17)

где,  – модуль зубчатой передачи

Определим делительные диаметры

                                             (4.18)

Делительное межосевое расстояние

                                         (4.19)

Коэффициент воспринимаемости смещения

                                          (4.20)

где,  – межосевое расстояние,

 – делительное межосевое расстояние,

Коэффициент уравнительного смещения

                                        (4.21)

Определим радиусы начальных окружностей

                                        (4.22)

Радиусы вершин зубьев

                                (4.23)

где,  – коэффициент высоты головки зуба

Радиусы впадин зубьев

                               (4.24)

где,  – коэффициент радиального зазора

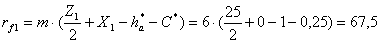
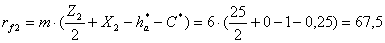
Высота зуба

                                           (4.25)

Толщины зубьев по делительной окружности

                          (4.26)

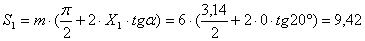
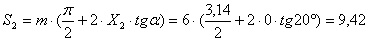
Радиусы основных окружностей

                                         (4.27)

Углы профиля в точке на окружности вершин

                                            (4.28)

Толщины зубьев по окружности вершин

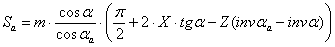         (4.29)

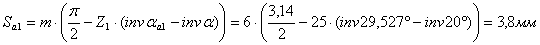
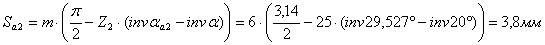
Проверим зубья на заострение

                                           (4.30)

 Зубья удовлетворяют условию заострения

Угловой шаг зубьев

                                               (4.31)

2.1 Определение скоростей

Для заданной схемы механизма строим 12 положений.

Определяем масштабный коэффициент построения механизма:

                                                        (2.1)

где, – масштабный коэффициент,

 – длина звена,

 – длина звена на чертеже,

Запишем длинны звеньев механизма на чертеже

Приступаем к построению повёрнутых планов скоростей для каждого положения. Рассмотрим пример построения для положения №5:

У кривошипа определяем скорость точки А

                                         (2.2)

где,  – длина звена,

 – угловая скорость кривошипа,

Для построения вектора скорости точки А определяем масштабный коэффициент

                                             (2.3)

где,  – скорость точки А,

 – вектор скорости точки А,

 – полюс, выбираемый произвольно

Для определения скорости точки B запишем систему уравнений:

                                         (2.4)

 – из задания

Для определения скорости центра масс 2-го звена S₂ воспользуемся соотношением:

                                                (2.5)

где, , – расстояния между соответствующими точками на механизме, м

,  – длинны векторов скоростей на плане, мм

 мм

Соединив, точку  и π получим скорость центра масс второго звена.

Для определения скорости точки C запишем систему уравнениё:

                                                (2.6)

 – из задания

Для определения скорости центра масс 4-го звена S₄ воспользуемся соотношением:

                                                (2.7)

где, , – расстояния между соответствующими точками на механизме, м

,  – длинны векторов скоростей на плане, мм

 мм

Соединив, точку  и π получим скорость центра масс второго звена.

Определим значения угловых скоростей звеньев.

Направление  определяем, перенеся вектор ab в точку S₂ – второе звено вращается против часовой стрелки. Аналогично получим, что  направлена по часовой стрелке.

Скорости точек остальных положений определяются аналогичным образом. Все значения сводим в таблицу(2.1).

Структурный анализ рычажных механизмов

Проводя исследование рычажного механизма следует уделять внимание возможности выбора двух основных направлений, одно из которых связано с непосредственным анализом, другой синтезом. Оба понятия существенно отличаются друг от друга, что нужно учитывать

Структурный анализ – процесс определения структурных особенностей, который может заключаться в следующем:

1. Определении кинематической пары.
2. Изучение структур групп.
3. Определение особенностей связи кинематической цепи.

Сегодня анализ проводится для определения дефектов структуры, которые в дальнейшем при необходимости могут устраняться.

Каждый случай исследования по-своему уникален

В рассматриваемом случае уделим внимание плоскому рычажному механизму, характеризующийся нерациональной структурой. Его особенности заключаются в нижеприведенных моментах:

1. Работоспособность механизма сохраняется исключительно при определенном соотношении длины звеньев. Образующаяся фигура в ходе построения напоминает параллелограмм.
2. Для исключения вероятности эксплуатации устройства с дефектами следует точно знать о наличии или отсутствии избыточных взаимосвязях, возможности пассивного распространения и их количества. Стоит учитывать, что они могут возникать исключительно в кинематических цепях замкнутого контура.
3. На сегодняшний день выделяют два основных типа контуров: замкнутые и зависимые. Независимым считается вариант исполнения, у которого хотя бы один элемент контура отличается от других.

Зависимые варианты исполнения дублируют друг друга. Для определения числа контура применяется специальная формула.

Также для исключения вероятности появления дефекта проводится расчет количества структурных групп и некоторые другие моменты. В общем можно сказать, что проводимый анализ направлен на достижение следующих задач:

1. Построение различных механизмов. При этом проводится определение подвижности и маневренности, так как подобные параметры считаются основными.
2. Создание плоских механизмов. Процедура подразумевает анализ состава структуры, а также определяет подвижности.

В целом можно сказать, что преследуемые цели зачастую направлены на определение возможной деформации структуры. Провести полноценный анализ можно только при всестороннем рассмотрении механизма.

Простой механизм блок

Рассматривая правила рычага, полезно сказать несколько слов о еще одном простом механизме – блоке. Представляет он собой обычный цилиндр с осью вращения, который имеет углубление по периметру своей боковой поверхности. Пример использования неподвижного блока показан ниже.

Как видно, выигрыша в силе и пути не происходит, однако неподвижный блок позволяет изменить направление воздействующей силы F.

Применение правила равновесия рычага к блоку производят, когда требуется рассчитать выигрыш в силе при использовании подвижных блоков. Один такой блок позволяет выиграть в 2 раза в силе и во столько же раз проиграть в пути.

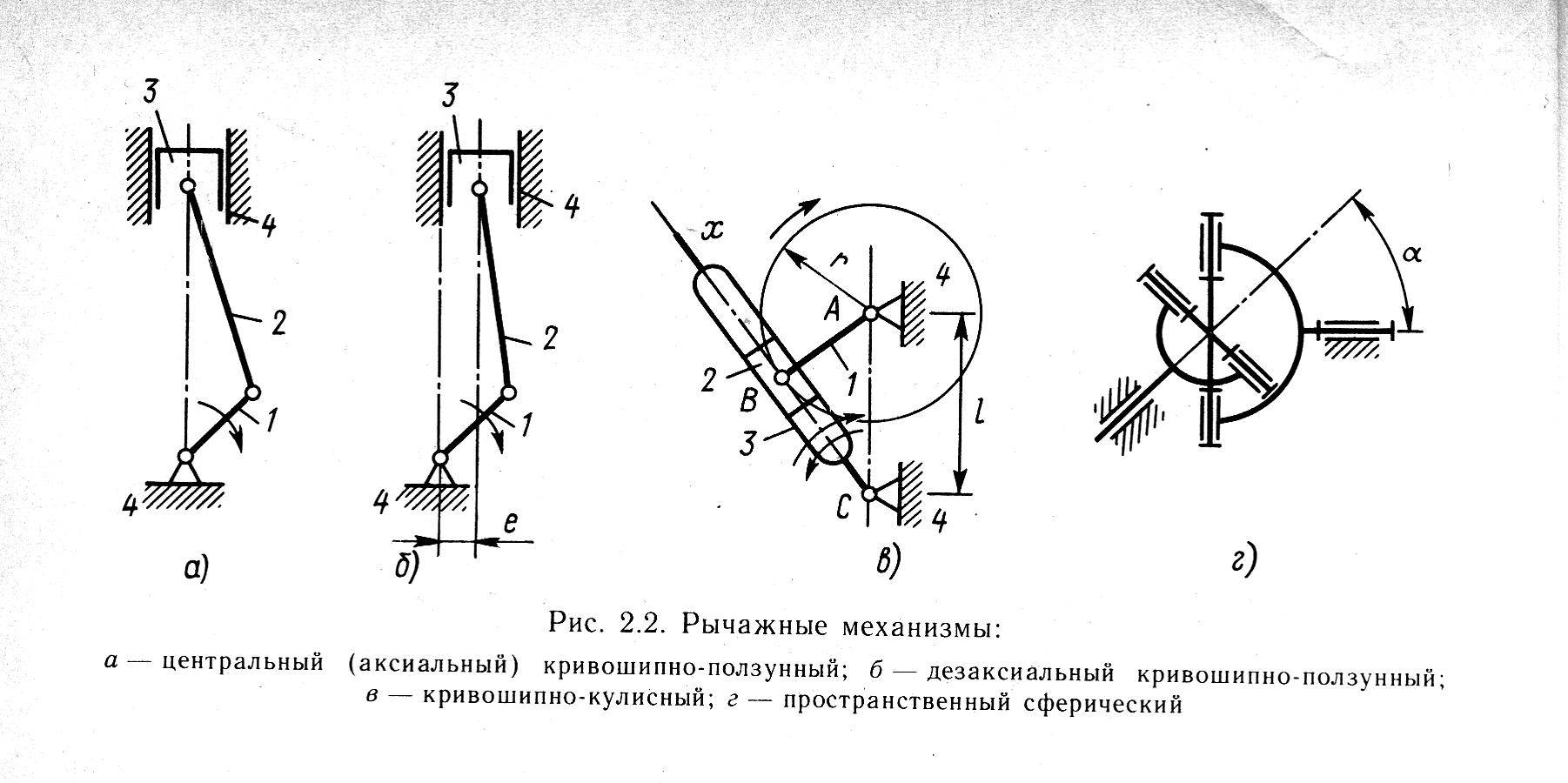
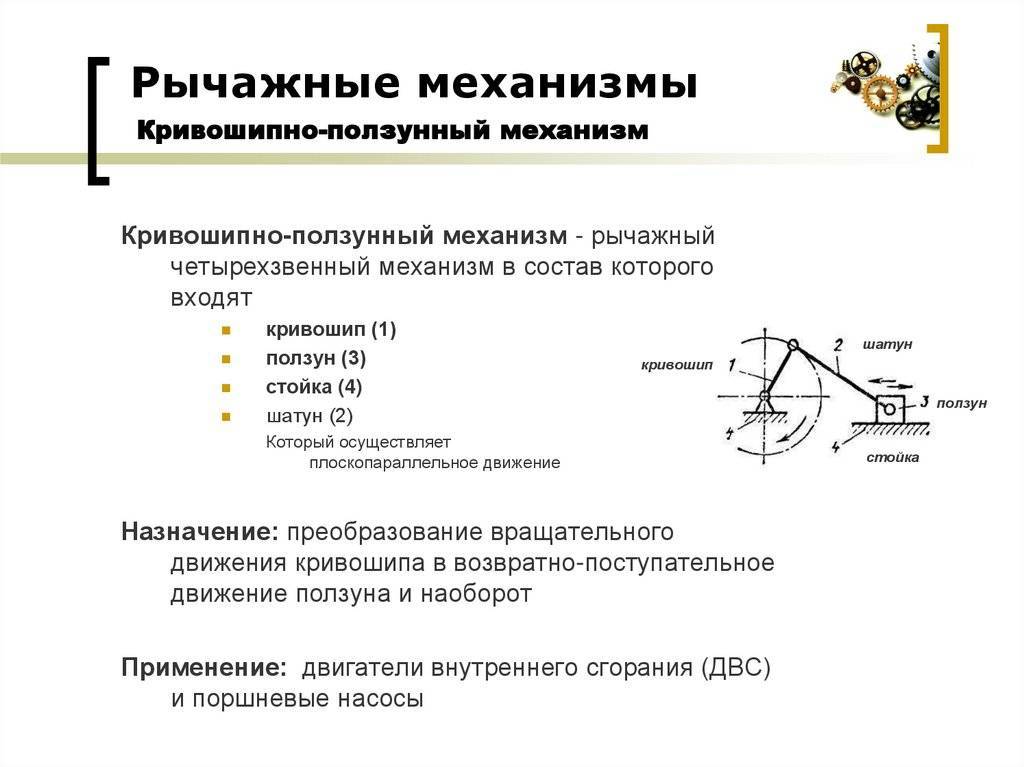
Расчет рычажного механизма

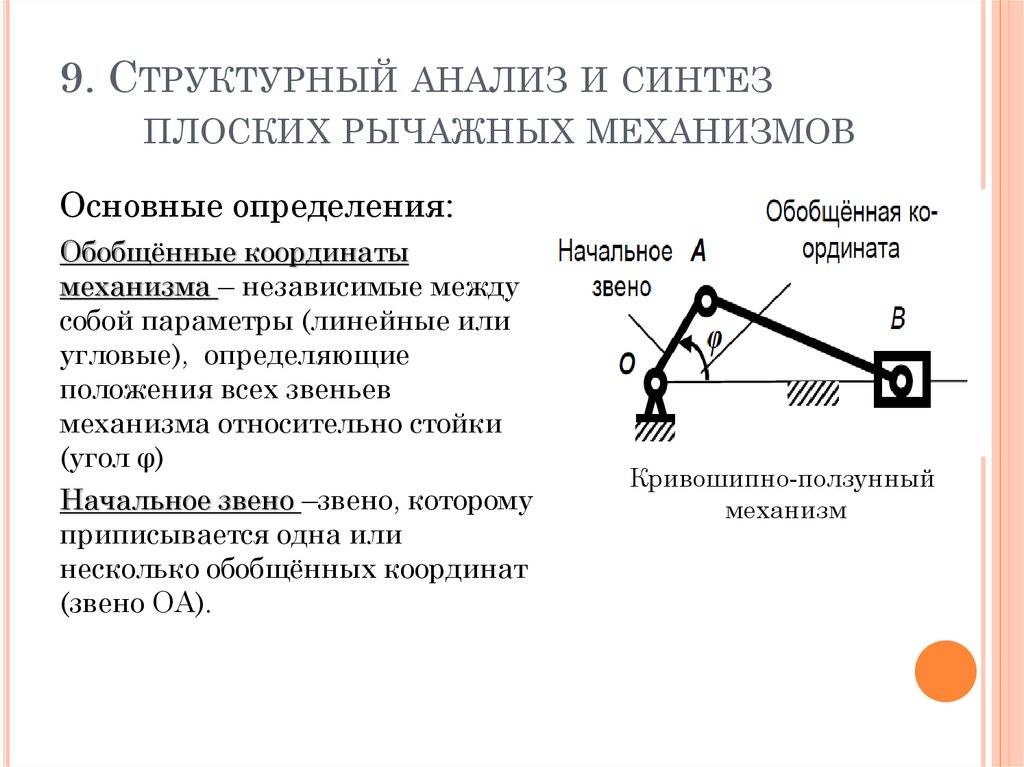
1. СТРУКТУРНЫЙ АНАЛИЗ И СИНТЕЗ РЫЧАЖНОГО МЕХАНИЗМА

.1 КИНЕМАТИЧЕСКАЯ СХЕМА

Рисунок 1.1 – Кинематическая схема технологической машины

= 0,25 м;= 0,80 м;= 0,62 м;= 0,70 м;

α = 19°;

β = 48°;

γ = 61°

1.2 СТРУКТУРНАЯ СХЕМА

Рисунок 1.2 – Структурная схема механизма 0 -стойка, 1 -кривошип, 2
-шатун, 3 -коромысло

Таблица кинематических пар

Таблица 1.1

Обозначение	Звенья образующие пару	Тип	Класс	Относительно движение звеньев
O	0,1	Низшая	5	Вращательное
A	1,2	Низшая	5	Вращательное
B	2,3	Низшая	5	Вращательное
C	0,3	Низшая	5	Вращательное

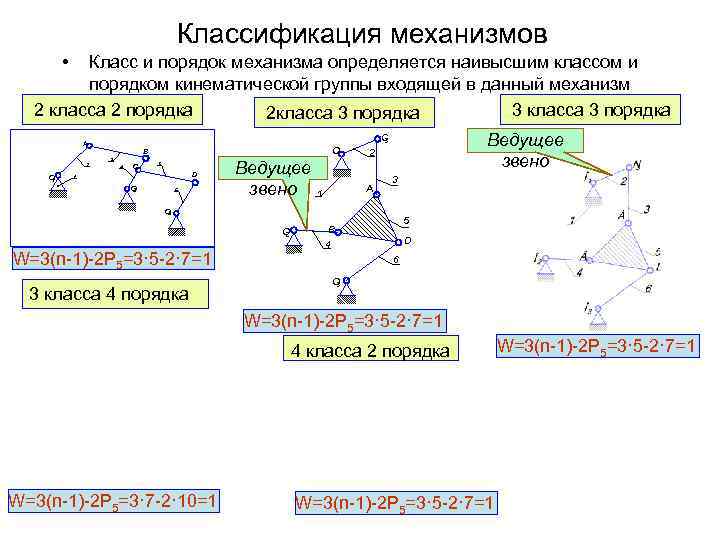
Подвижность механизма по формуле Чебышева

=3n – 2p5 – p4 + qпс

где n – число подвижных звеньев;- количество пар 5 класса (по таблице
1.1);- количество пар 4класса (по таблице 1.1);

qпс – число пассивных связей.

=3*3 – 2*4 – 0 + 0 = 1

В механизме одно входное звено.

Расчленяем механизм на простейшие структурные составляющие (рисунок
1.3).Звено 3 является выходным, поскольку к нему приложена сила полезного
сопротивления Fпс. Тогда звено 1 – входное, а звено 2 – промежуточное.

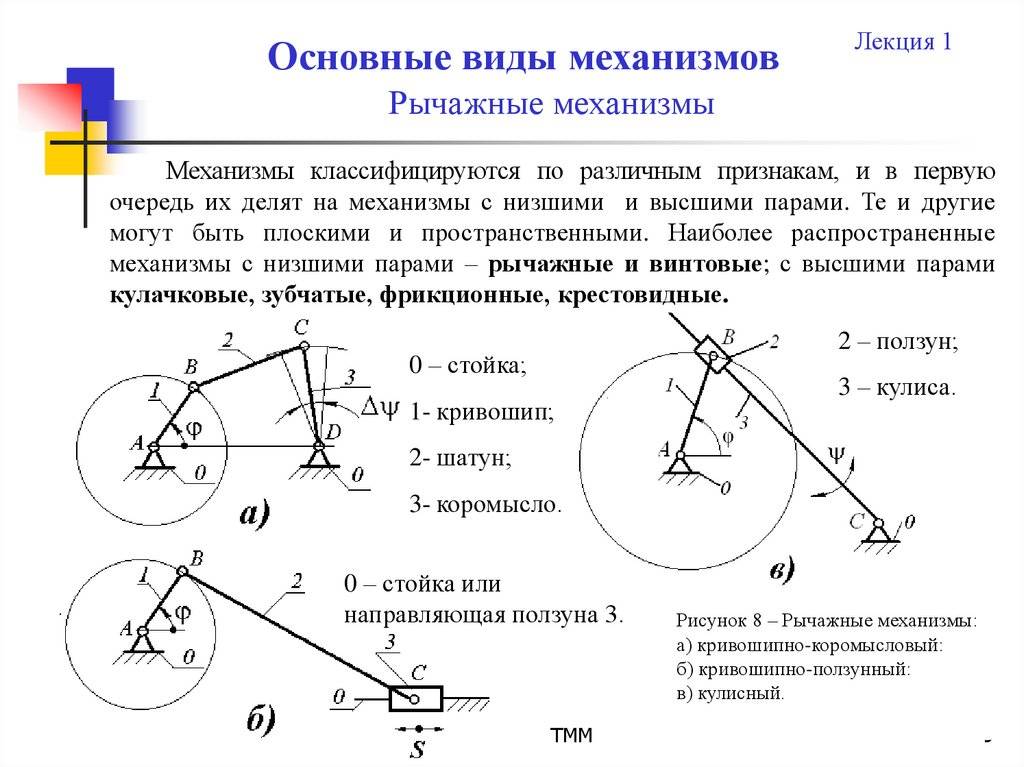
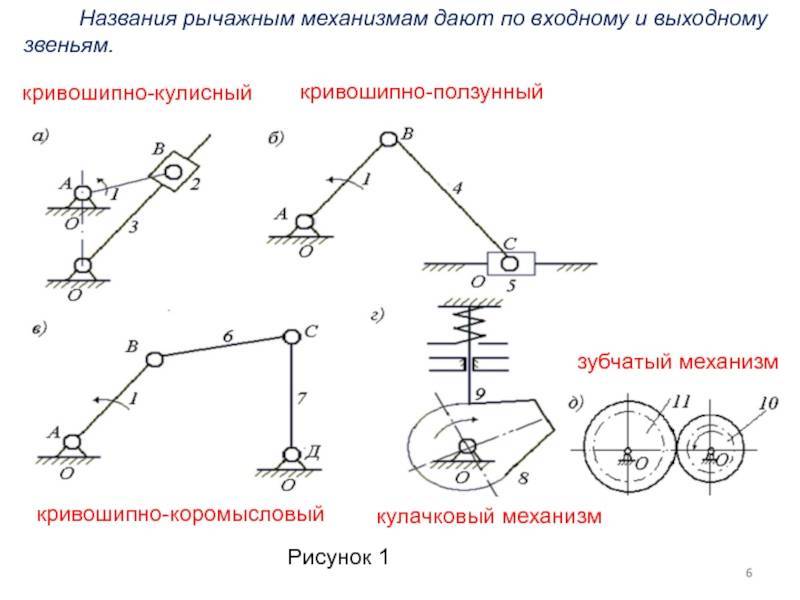
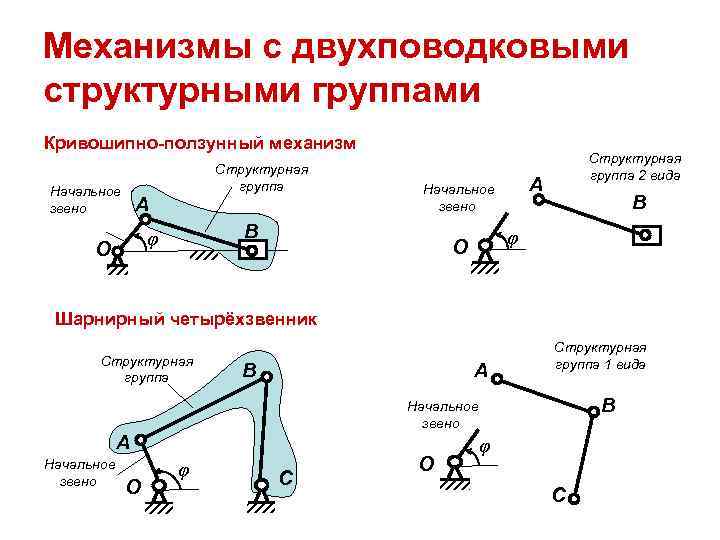
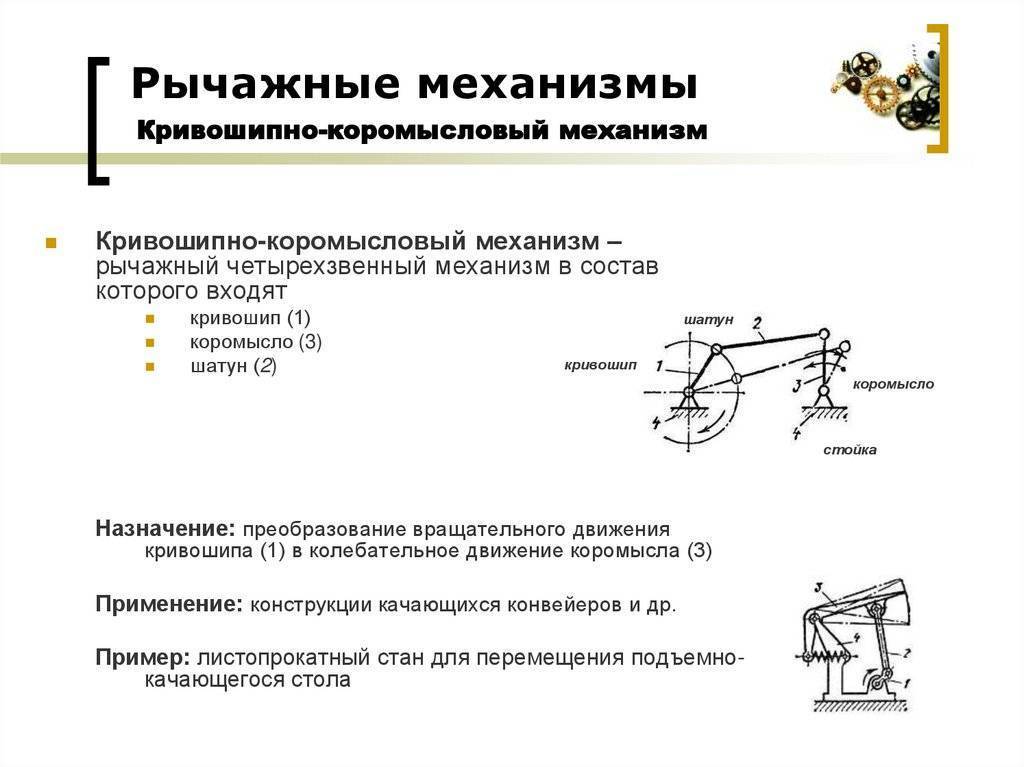
Шарнирно-рычажные механизмы

Подобный тип механизма также получил весьма широкое распространение. При этом за его длительный срок эксплуатации было изобретено несколько вариантов исполнения, которые характеризуются своими определенными свойствами. Выделяют следующие виды шарнирно рычажных механизмов:

1. С двумя кривошипами.
2. Кривошипно-коромысловые.
3. Двух коромысловые.

Примером использования варианта исполнения с двумя кривошипами можно назвать перенос тяжелой заготовки с тележки на обрабатывающий станок. Его конструкция характеризуется следующими особенностями:

1. В качестве основы применяется две четырехлучевые звездочки, которые фиксируются на валу.
2. Также фиксация осуществляется за счет шарнирного соединения с осью и четырьма ложементами. На момент воздействия усилия они создают двухкривошпный механизм, который принимает часть нагрузки.
3. Валы фиксируются на подшипниках скольжения, которые расположены в корпусе. При помощи кронштейна они устанавливаются на общей раме, принимающую основную нагрузку.

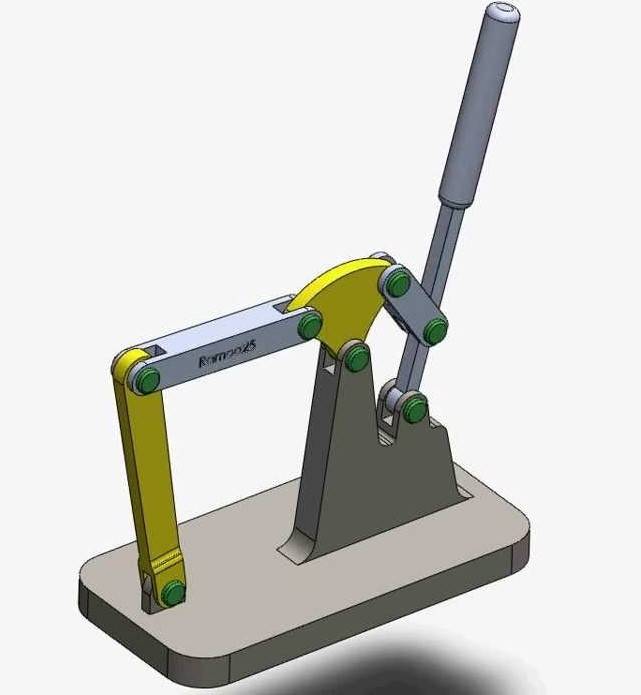
Именно конструктивные особенности во многом определяют то, где и каким образом может применяться устройство.

Возможные проблемы и важные особенности

При работе рассматриваемого механизма велика вероятность возникновения самых различных проблем. Примером можно назвать проскок положения максимума и многие другие. Для предотвращения проблем следует:

1. Проводить своевременное обслуживание.
2. Соблюдать технику безопасности.
3. Выполнять периодическую замену различных деталей.

Также следует уделять внимание тому, какой период смазки коленно-рычажного механизма. Только при своевременной подаче смазывающего вещества можно существенно снизить степень износа основных элементов

Стоит учитывать, что для рассматриваемого рычажного механизма требуется специальная жидкость, обладающая особыми свойствами.

Проскок положения максимума

Как выше было указано, довольно большое распространение получил случай проскока положения максимума. Среди особенностей этого момента отметим следующее:

1. На момент, когда все три шарнира находится на одной линии оказывается наибольшее усилие смыкания.
2. В данном положении шток вытянут максимально, неосторожные действия могут стать причиной повреждения конструкции.
3. Если конструкция была настроено неправильно, то серьги проскакивают положение крайней точки. Подобное явление становится причиной, по которой шток не может вернуться в первоначальное положение.

На момент максимального перемещения штока оказывается сильное давление, за счет чего возникает вероятность деформации основных элементов. Именно поэтому проскок положения максимума приводит к механическому повреждения станка.

Оверлок

Проблема может возникать также в случае неправильной регулировки рычажного механизма. Примером можно назвать случай, когда усилия цилиндра недостаточно для открытия основных элементов. Особенности проблемы следующие:

1. На колонны в большинстве случаев надеваются ленточные нагреватели.
2. За счет нагрева до определенной температуры происходит удлинение колонны, за счет чего снижается степень оказываемой нагрузки.

В подобном случае запрещается открывать форму до полного открытия колонн. Это связано с тем, что возникающая нагрузка может стать причиной деформации направляющих элементов. Если они потеряют свою форму, то в дальнейшем существенно усложниться ход подвижных элементов.

Как рассчитать простой рычажный механизм самостоятельно?

Перед непосредственным созданием механизма следует провести расчеты основных показателей, а также построить схему распределения нагрузок. Силовой расчет рычажного механизма проводится после определения исходных данных:

1. Создается кинематическая схема массы и моментов, инерции звеньев и положения центров массы.
2. Учитывается закон движения механизма.
3. Определяется внешнее силовое нагружение.
4. Рассчитывается угол перекрытия рычажном механизме.

Проводимый кинематический и силовой предусматривает создание системы координат, которая используется для расчета кинематических характеристик. Кулисно-рычажный вариант исполнения проектируется при создании системы координат и обозначением всех сил. Для проектирования требуется большое количество различных формул, при этом в конце следует выполнить проверку.

Как правило, рассматриваемая работа выполняется инженерами, который учитывают ГОСТ проектирование. Это связано с тем, что структурная формула плоских рычагов выбирается в зависимости от области их применения.

Устройство и принцип действия одинарного механизма смыкания

Подобный агрегат представлен сочетанием нескольких конструктивных элементов, за счет которых обеспечивается передача и увеличение усилия. Основными деталями можно назвать:

1. Две неподвижные траверсы. Их соединение проводится при помощи цилиндрической колонны.
2. Крепление проводится при помощи гаек и контргаек, которые существенно повышают прочность конструкции.
3. Передача усилия осуществляется за счет гидравлического цилиндра. Его крепление проводится при помощи шарниров.
4. Также есть серьги.

Принцип действия механизма достаточно сложный. Характеризуется он следующим образом:

1. Смещение поршня вниз в гидравлическом блоке происходит выпрямление серьги, она совмещается с горизонтальной осью.
2. В результате совмещения осей происходит соединение шарниров.
3. Шарниры монтируются так, чтобы при контакте расстояние между ними было меньше, чем суммарная длина обеих серег.
4. Выпрямление серег происходит за счет распорного усилия.

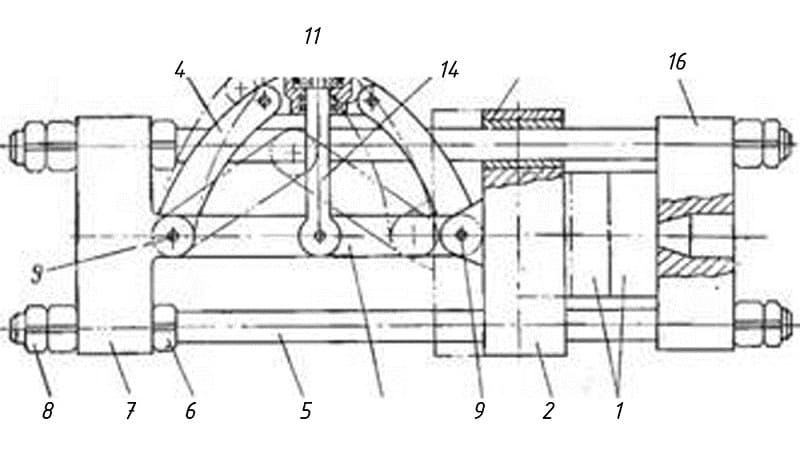
Приведенная выше информация определяет то, что главным недостатком конструкции становятся нескомпенсированные боковые усилия, которая возникают из-за нагрузки втулок и колонн. Именно поэтому рекомендуется использовать подобный вариант исполнения только в случае передачи небольшого усилия.

Золотое правило механики

Все примеры простых механизмов, которые мы рассмотрели, имеют одно общее свойство, которое называют золотым правилом механики: 

Во сколько раз мы выигрываем в силе, во столько же раз проигрываем в перемещении.

Произведение силы на перемещение в механике называется работой и обозначается буквой А:

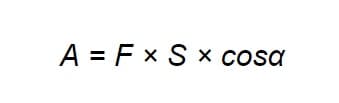
где α — угол между векторами силы и перемещения. Если направления векторов совпадают, формула работы выглядит проще: A = F × S. 

Сэкономить в силе больше, чем проиграть в перемещении — то есть выиграть в работе — не позволяет ни один механизм. Чем меньше силы нужно потратить при подъёме тела по наклонной плоскости, тем длиннее должна быть эта плоскость. Чем меньше сил нужно для воздействия на рычаг — тем длиннее должно быть его плечо.

«Дайте мне точку опоры, и я переверну Землю» — заявил Архимед. Теоретически он мог бы поднять груз, равный нашей планете, выбрав рычаг подходящей длины. Масса земли — примерно 6 000 000 000 000 000 000 000 тонн, в то время как человек в среднем способен поднять груз около 60 килограммов. А значит, плечо силы должно быть больше плеча груза в 100 000 000 000 000 000 000 000 раз. Поэтому чтобы плечо груза сдвинулось хотя бы на один сантиметр, учёному пришлось бы сдвинуть плечо силы на 1000 000 000 000 000 000 км. Даже со скоростью движения в 1 м/с на это ушло бы тридцать тысяч миллиардов лет.

Качественные показатели рычажных механизмов

Для формирования общего описания устройства применяются различные качественные показатели, которые могут касаться самых различных моментов. Наиболее распространенными можно назвать:

1. КПД считается наиболее важным параметром, который рассматривается при создании самых различных механизмов. Эта безразмерная величина определяет количество энергии, которая применяется для достижения поставленных целей с учетом потерь. Стоит учитывать тот момент, что подобный показатель рычажного механизма находится всегда меньше единицы, то есть при работе возникают потери. При приближении значения КПД к единице существенно снижаются потери, а также повышается качество рычажного механизма. Провести расчет рассматриваемого показателя достаточно сложно, так как для этого требуются самые различные формулы.
2. Ход механизма также учитывается при проектировании подходящего устройства. Ход определяется начальной и конечной точкой. При этом стоит учитывать, что в некоторых случаях провести расчеты достаточно сложно, так как траектория движения может быть криволинейной.
3. Угол размаха коромысла измеряется путем вычитания двух крайних точек положения на момент работы. В большинстве случаев устройство совершает повторяющееся цикличное движение.
4. Коэффициент, отражающий неравномерность распределения средней скорости. Этот показатель определяется соотношением времени холостого хода к рабочему. Провести соответствующие расчеты можно только при применении формул, а также построении чертежа.
5. Угол давления и передачи. Подобный параметр представлен соотношением острого угла между векторной активной силы, которая действует на предшествующем звене.

Каждый параметр рассматриваемые в отдельности, после чего составляется оценочный анализ, отражающий общее состояние механизма.

Перечень неисправностей КШМ

Главные неприятности, которые могут случится с кривошипно-шатунным механизмом:

1. Как шатунные, так и коренные шейки коленчатого вала подвержены износу и механическим повреждениям.
2. Износ, механические повреждения и даже расплавление могут угрожать и вкладышам (подшипникам) шеек коленвала.
3. «Болезни» поршневых колец – это закоксовывание не до конца сгоревшими продуктами горения (углеводороды окисляются только до углерода), их залегание и даже поломки, что может привести к фатальным последствиям.
4. Цилиндропоршневая группа также подвержена износу. В современных «движках» это не так заметно, всё-таки они созданы по последнему слову техники, но у каждой детали имеется конечный ресурс.
5. На днище поршня может отложиться нагар.
6. В деталях могут появиться трещины, они могут прогореть, обломиться и даже расплавиться.
7. Двигатель может даже заклинить.

Перечень неисправностей КШМ

Главные неприятности, которые могут случится с кривошипно-шатунным механизмом:

1. Как шатунные, так и коренные шейки коленчатого вала подвержены износу и механическим повреждениям.
2. Износ, механические повреждения и даже расплавление могут угрожать и вкладышам (подшипникам) шеек коленвала.
3. «Болезни» поршневых колец – это закоксовывание не до конца сгоревшими продуктами горения (углеводороды окисляются только до углерода), их залегание и даже поломки, что может привести к фатальным последствиям.
4. Цилиндропоршневая группа также подвержена износу. В современных «движках» это не так заметно, всё-таки они созданы по последнему слову техники, но у каждой детали имеется конечный ресурс.
5. На днище поршня может отложиться нагар.
6. В деталях могут появиться трещины, они могут прогореть, обломиться и даже расплавиться.
7. Двигатель может даже заклинить.

Деталь – элементарная часть машины, которая выполнена из однородного материала или не может быть разобрана на более простые части (зубчатое колесо, валы, болты).

Различают детали общего

(встречаются в большинстве машин) и специального
(встреча-ся в спец-х,
особых машинах) назначения.

Твёрдые тела, составляющие
механизм называют звеньями
. Звено может состоять из нескольких деталей,
соединённых неподвижно.

Стойка
– неподвижное звено.

Совокупность двух звеньев
имеющих относительное движение называют кинематической парой
.

Условия существования к.п.:

1.
Наличие двух звеньев.

2.
Непосредственный контакт.

3.
Возможность относительного
движения.

Коромысло
– звено, совершающее вращательное движение.

Бывают вращательные,
поступательные к.п.. Звенья могут соприкасаться между собой в точке, по линии
или по поверхности (образуя к.п.). К.п. накладывают ограничения на
относительное движение звеньев. Эти ограничения называют связями
.

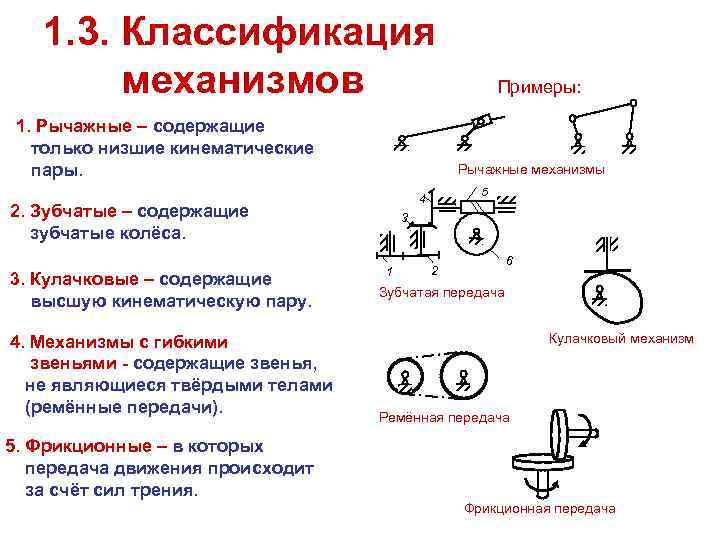
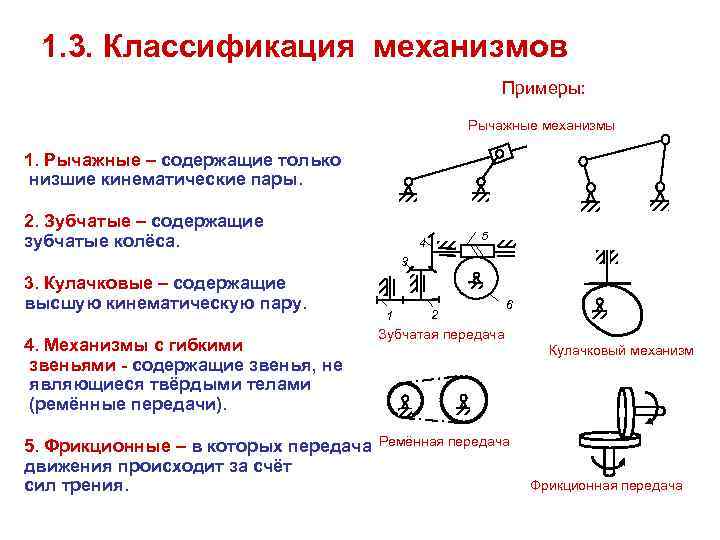
3.Классификация
кинематических пар.

К.П.
– совокупность 2-х звеньев, имеющих относит. движ.

Услов.сущ.к.п.:-наличие 2 звеньев

Непосредств.контакт

Возмож.относ.движ.

Звенья могут соприкос.между
собой, образ.к.п.в точке, по линии, по плоскости.

К.п. наклад.огранич.на
относит.движение звеньев. Эти огранич.назыв.связями.

К.п. классифиц.по:

1.по виду элементов соприкосновения

если
элем.соприкоснов.-поверхность,то к.п.низшая.

если контакт звеньев по
линии или в точке,то к.п.высшая.

2.по хар-ру относит.движения
звеньев –плоские

Пространственные

3.по числу связей, накладыв.на
относит.движ.звеньев:1,2,3,4,5 класса

4.Кинематические цепи
.

Сочетания звеньев вх-х в
кин-ую пару наз-т кин-ой цепью. КЦ бывают простые, сложные, замкнутые,
разомкнутые. Мех-зм – такая КЦ в кот при заданном движ-ии одного или неск-х
ведущих звеньев остальные движ-ся вполне опред-ым образом. Все звенья делятся
на 3 группы: 1-Группа ведущих звеньев. З-н движ-я в ведущих звеньях обычно
задается. 2-Ведомые звенья. З-н движ-я ведомых звеньев зав-т от з-на движ-я
ведущих звеньев. 3-Стойка мех-зма. Плоским мех-ом наз такой мех-зм, звенья кот.
движ-ся в одной или неск-х // пл-ях. W=3n-2p 5 -p 4 – степень
подвижн-ти плоского мех-зма, где W-число степеней подвижности, должно соотв-ть числу
ведущих звеньев, n-число подвиж-х звеньев, p 5 число пар 5-го класса (соотв-о p 4).

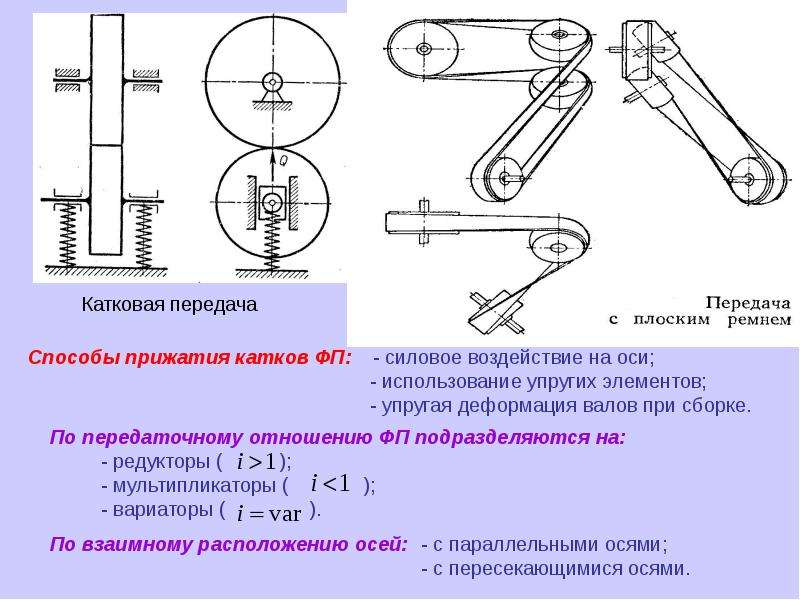
5. Фрикционные
передачи(механизмы)

Передача основана на
использовании сил трения

Преимущества:

·
Простота, безступенч. регулирование
перед. числа

·
Плавность бесшумность работы
передачи

·
Надёжность соединения

·
При перегрузке происходит
проскальзование катков, это предохраняет механизм от поломки

Недостатки:

·
Большие давления на валы и опоры

·
Износ рабочих поверхностей

·
Непостоянство передаточного числа
(из-за проскальзывания катков)

·
Небольшая нагрузочная способность
до 20 кВт

Передачи классифицируют:

1. По расположению валов

а) циллиндрическая(оси | |)

б) оси пересекаются – передача
коническая

в) оси перекрещиваются –
передача реечная

Для повышения нагрузочной
способности катки изготовляют клинчатыми

2. По характеру силы
прижатия катков:

а) с постоянной силой прижатия

б) с переменной силой прижатия

В зависимости от передоваемой
нагрузки, чтобы обеспечить непосредственный контакт катков сила прижатия
автоматически изменяеться.

3. Передачи делятся на:

а) с условно-постоянным
передаточным числом

б) с переменным передаточным
числом (вариаторы)

Fтр>F(вн нагр.)

Qf=kF Q=kF/f – сила нажатия

к – кооф. запаса сцепления

f – кооф. трения скольжения

Передачи с плавнорегулируемым
передаточным числом назыв вариаторами

По конструкции вариаторы
разнообразны

Область применения

Рычажные механизмы получили весьма широкое применение, что прежде всего можно связать с их преимуществами перед другими устройствами, которые устанавливаются для транспортировки грузов и иной передачи усилия

Рассматривая область применения следует уделить внимание следующим моментам:

1. Чаще всего рычаг устанавливается для подъема груза. Он является неотъемлемым элементом достаточно большого количества различных устройств, которые приводятся в движение ручной силой.
2. Встречаются в производственных цехах, в химической промышленности, в машиностроении и многих других отраслях.
3. Область применения ограничивается типом применяемого материала при изготовлении основных частей, принципом действия, а также максимальной возможной нагрузкой, которая оказывается на рабочий орган.

Сегодня рычажные механизмы получили весьма широкое распространение, могут применяться при создании различного оборудования. При этом если важна экономия, то рычаг можно создать своими руками.

В заключение отметим, что провести самостоятельно проектирование рычага достаточно сложно. Это связано с необходимостью применения достаточно большого количества различных формул, построением графиков соответствия и многими другими моментами. Допущенная ошибка может стать причиной повреждения механизма на момент эксплуатации, существенного снижения показателя КПД и возникновения многих других проблем.

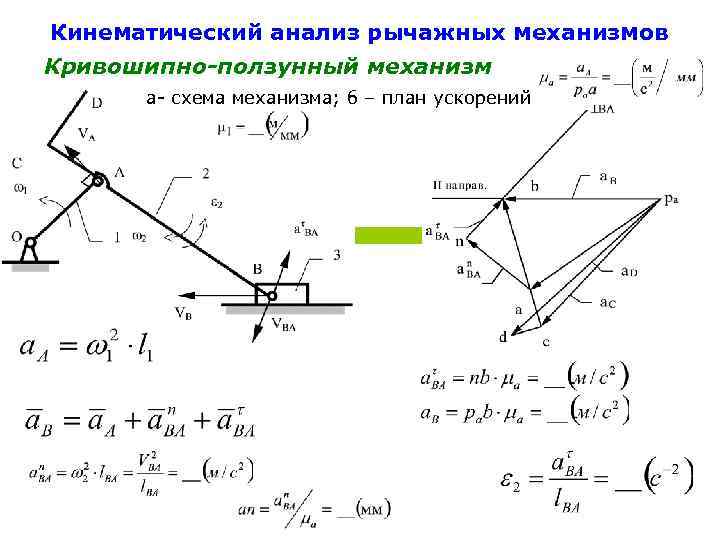
Кинематический анализ механизма

3.1. 
Аналитическое определение аналогов скоростей и ускорений

1)  Дифференцируя
уравнения геометрического анализа для группы I (кривошипа) по q, мы получаем
аналог скорости точки A:

Дифференцируя уравнения второй
раз, мы получаем аналог ускорения точки A:

2)  Дифференцируя
первое уравнение геометрического анализа для группы ВПВ по q,
мы получаем следующее:

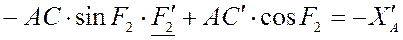
Напомним выражение для AC:

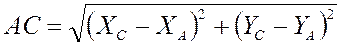
Тогда  .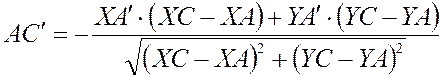

Сразу же определим :

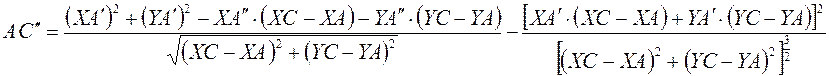
Отсюда мы можем найти аналог
угловой скорости :

Приведём к более удобному для
второго дифференцирования виду:

Дифференцируя уравнение второй
раз, мы получаем следующее:

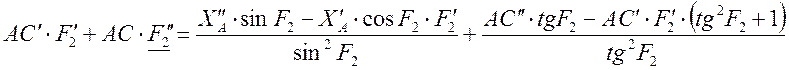
Отсюда мы можем найти аналог
углового ускорения :

5.2 ОПРЕДЕЛЕНИЕ НЕИЗВЕСТНОГО ЧИСЛА ЗУБЬЕВ ОДНОГО ИЗ КОЛЕС

Выделяем из механизма планетарную часть: сателлит 4
сцепляется одновременно с колесом 3 и с колесом 5. Оси вращения колес 3 и 5
совпадают с осью вращения водила Н, т.е. 3, 5 -центральные колеса. Т. о. 3, 4 и
5 – планетарная часть. 1, 2 – непланетарная часть. Т.к. одно из центральных
колес (колесо 5) неподвижно, механизм обладает одной степенью свободы. Проверим
это расчетом:

Условие соосности для планетарной части:

Неизвестное число зубьев колеса :

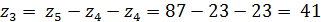
5.3 КИНЕМАТИЧЕСКИЙ РАСЧЕТ АНАЛИТИЧЕСКИМ МЕТОДОМ

Передаточное отношение не планетарной части механизма

В планетарной ступени требуется записать передаточное
отношение от водила к центральному колесу:

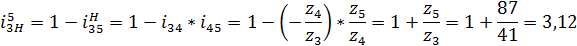
Передаточное отношение всего механизма

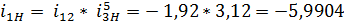
Ввиду того, что

угловая скорость входного колеса 1

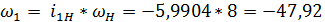
Найдем угловые скорости

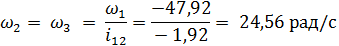
Найдем угловую скорость :

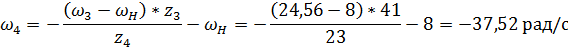
.5 ВЫЧЕРЧИВАНИЕ КАРТИНЫ ЗАЦЕПЛЕНИЯ

Выбираем для построения масштаб ЕСКД М4:1.

Проводим межцентровую линию и на расстоянии

Отмечаем на ней центры O₁и O₂.

Проводим на каждом колесе окружности: начальную, делительную,
основную, вершин и впадин. Для контроля измеряем радиальные зазоры между окружностями
вершин и впадин сопрягаемых колес с₁ = с₂ ≈ 7 мм.
Это соответствует с учетом масштаба расчетному заданию

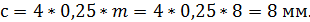
На межцентровой линии в точке касания начальных окружностей
отмечаем полюс зацепления W.

Проводим общую касательную к обеим основным окружностям и
убеждаемся в том, что она проходит через точку W.

Отмечаем на касательной точки касания N₁и N₂ – границы теоретической
линии зацепления

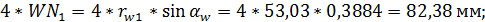
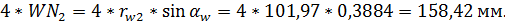
Проверка

Выделяем на линии зацепления активную часть ab заключенную между
окружностями вершин колес.

Строим приближенно эвольвентные профили, сопрягаемые в т. W
так, как описано в п.п. 1…8 на с.11

Строим оси симметрии зубьев, сопрягаемых в полюсе. Для этого
на делительных окружностях делаем засечки на расстояниях 0,5S от только что
построенных профилей в сторону их вогнутости и соединяем полученные точки с
центрами колес штрихпунктирными линиями. С учетом масштаба

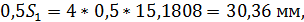
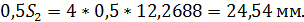
На расстоянии

по делительной окружности проводим оси симметрии двух
соседних зубьев.

Строим закругления ножек зубьев во впадинах радиусом

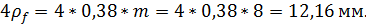
Выделяем рабочие поверхности профилей зубьев.

Строим графики удельных скольжений в масштабе  Абсциссы расчетных точек
графиков из табл. П.1.2 с учетом принятого масштаба для ρ_k1 М4:1, а также ординаты, вычисленные по формуле

ρk1 мм	20	40	60	80	100	120
мм	–94,79-32,2-11,33-0,95,369,53
мм	20	16,52	12,34	7,23	0,86	-7,33	-18,22
ρk1 мм	140	160	180	200	220	240,748
мм	12,52	14,75	16,49	17,88	19,02	20
мм	-33,44	-56,21	-99,96	-168,77	-387,81	–

Проставляем стандартные обозначения размеров.

Измеряем фактическую длину общей нормали шестерни

Вычисляем относительную погрешность с расчетным значением