Деформация растяжения-сжатия

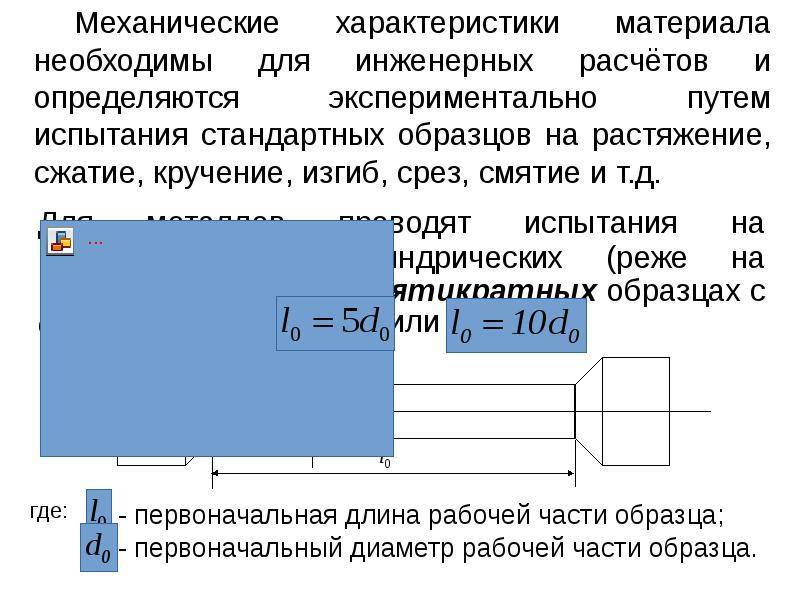
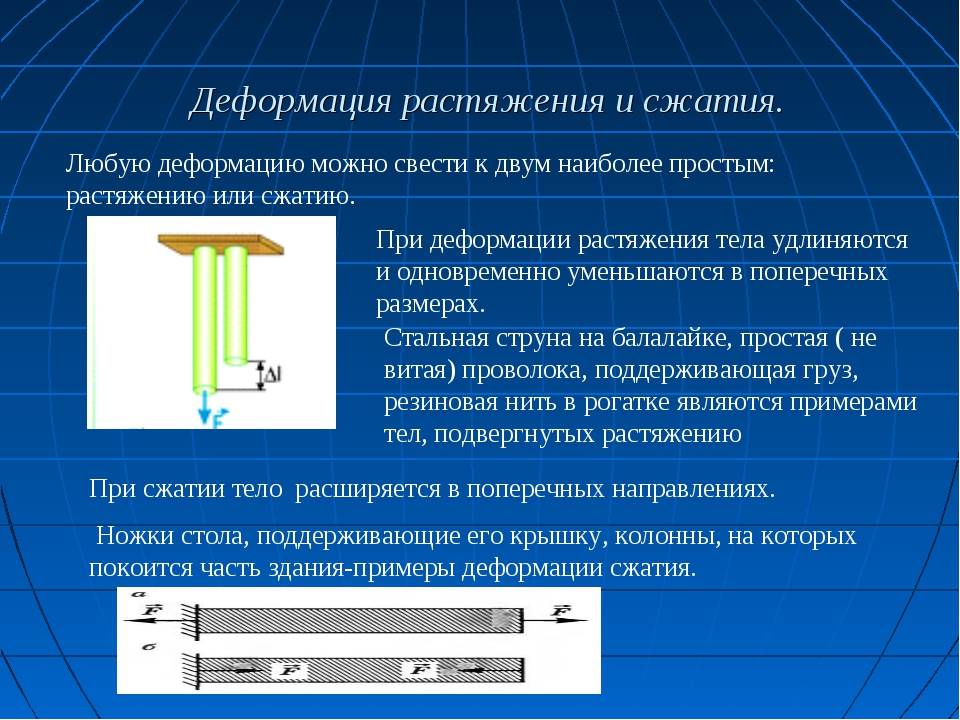
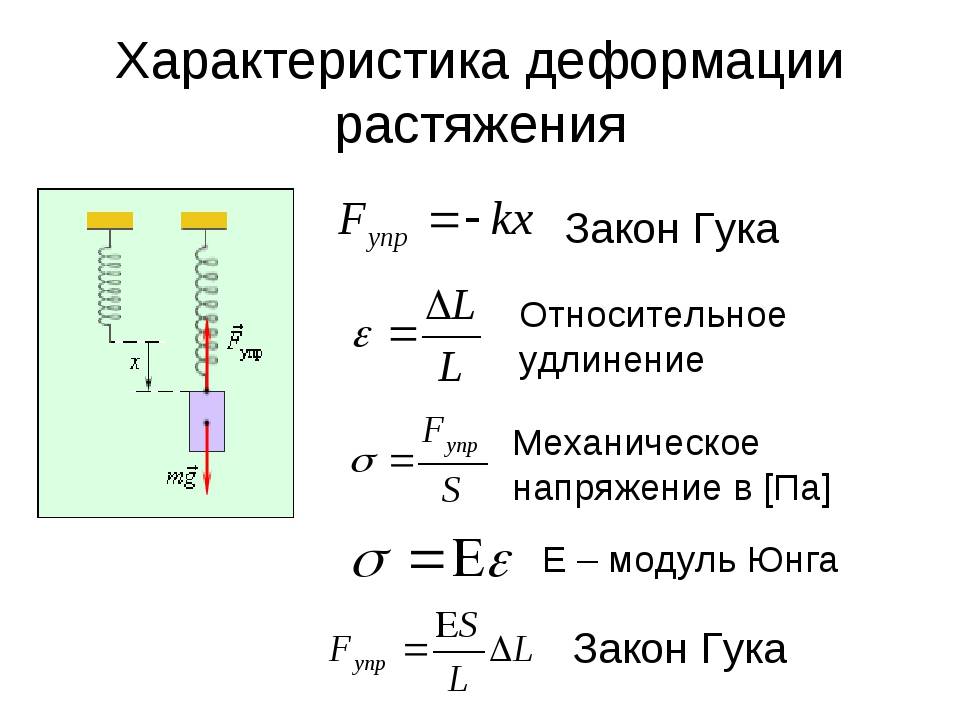
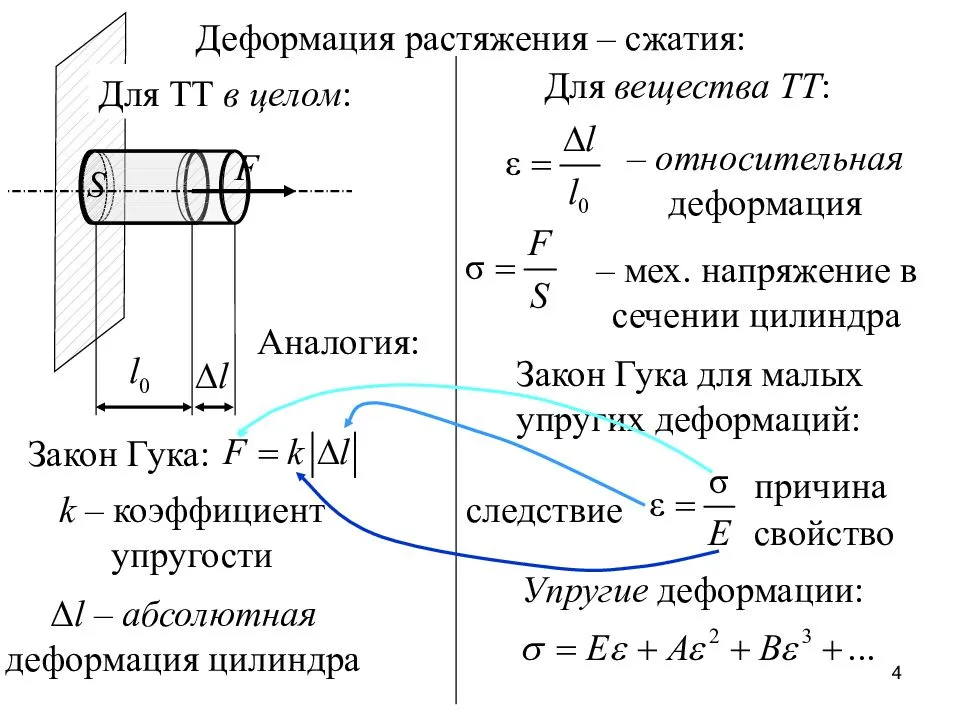
Расчёты на прочность при изгибе

Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом

Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта

Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.

Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.

Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:

• дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
• способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
• семейство принятых гипотез;
• разработанные правила построения графических изображений (построение эпюр).

Расчёт параметров производится в три этапа:

• при проверочном расчёте (вычисляют величину максимального напряжения);
• на этапе проектирования (производится выбор толщины и параметров сечения бруса);
• во время вычисления допустимой нагрузки.

Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.

Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей. При чистом изгибе эпюры имеют следующие особенности:

• на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
• на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
• в точке появления приложенного момента, скачок равен величине этого параметра;
• на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
• в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).

На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:

• расчёт производят с учётом нормальных напряжений;
• в качестве основного предположения принимают гипотезу о плоских сечениях;
• продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
• деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
• для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
• физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
• процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).

Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.

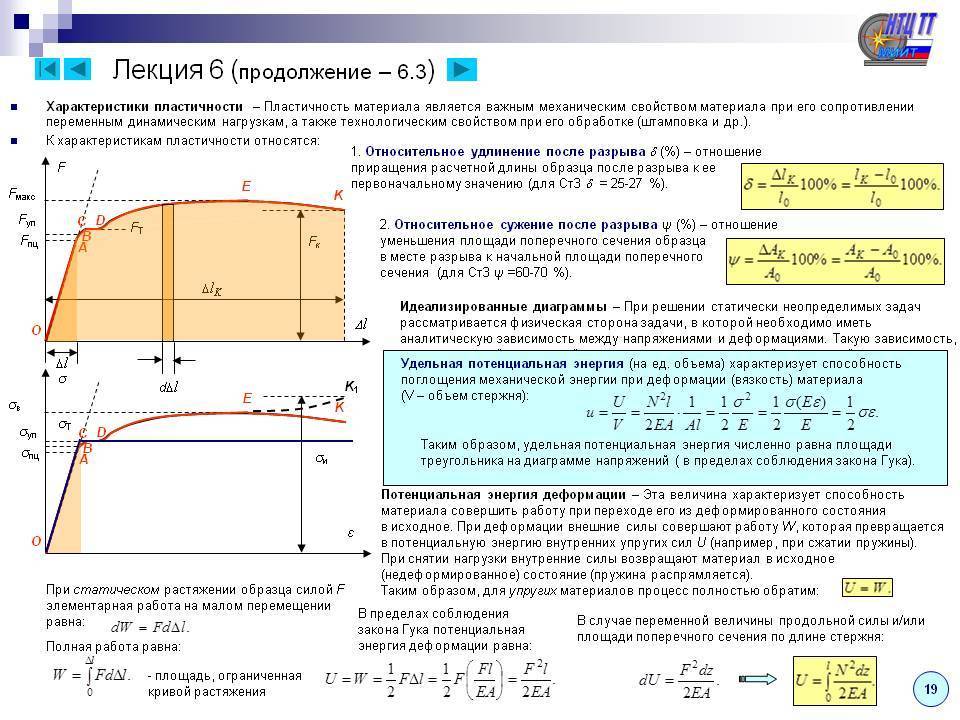
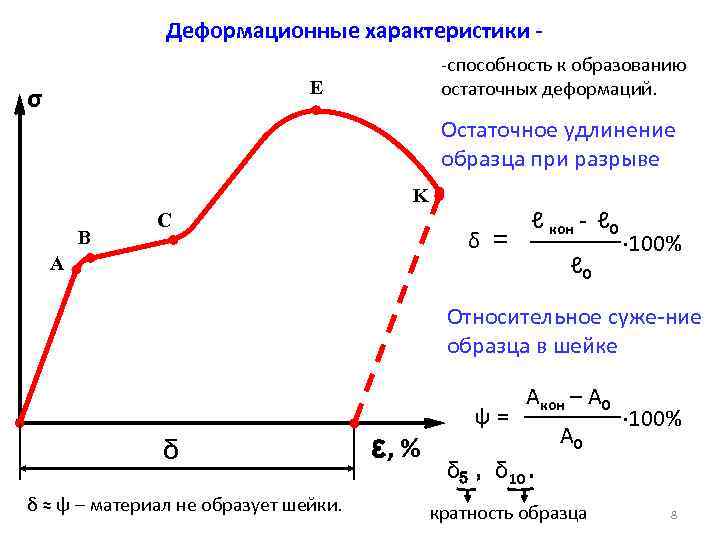
Предел прочности

Определение 9

Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.

В точке e материал разрушается.

Определение 10

Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.

Определение 11

Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.

Деформация сдвига имеет аналогичные закономерности и свойства. Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела. Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела). Для малых деформаций действует следующая формула:

∆xl=1GFS

Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Нм2, G=,42·1011 Нм2.

Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен. При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела

При малых деформациях

Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях

При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях

∆VV=1Bp

Буквой B обозначен коэффициент пропорциональности, называемый модулем всестороннего сжатия. Такому сжатию можно подвергнуть не только твердое тело, но и жидкость и газ. Так, у воды B=2,2·109 Нм2, у стали B=1,6·1011Нм2. В Тихом океане на глубине 4 км давление составляет 4·107 Нм2, а относительно изменения объема воды 1,8 %. Для твердого тела, изготовленного из стали, значение этого параметра равно ,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно. Газы могут сжиматься еще лучше, чем тела и жидкости.

От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.

Всё ещё сложно? Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

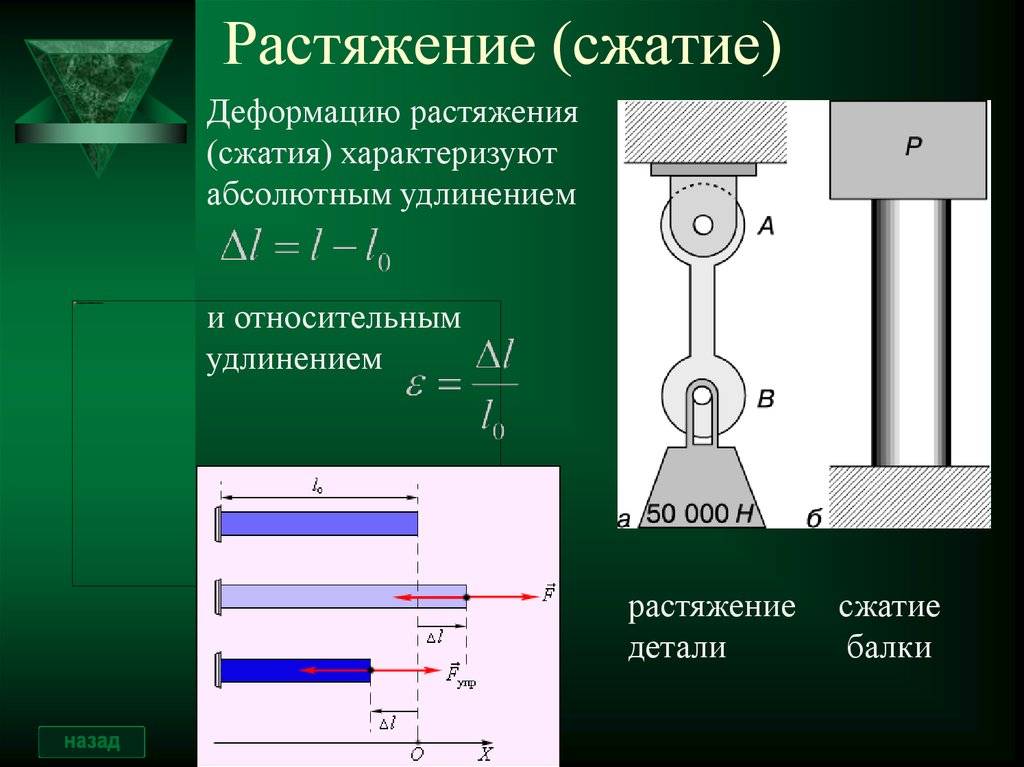
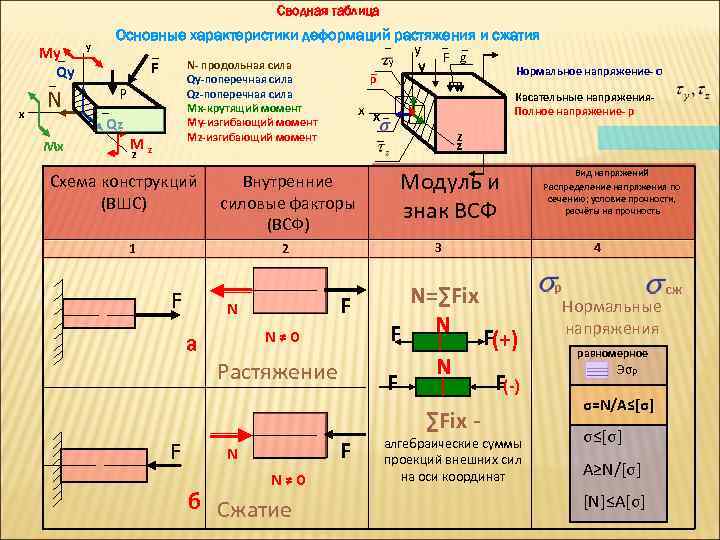
Напряжения при растяжении-сжатии.

Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.

Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

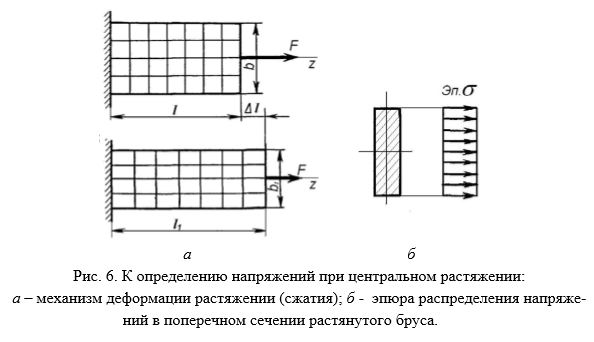
Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.

Техническая механика



Сдвигом называют такой вид деформации, при которой в любом поперечном сечении бруса возникает только поперечная сила. Деформацию сдвига можно наблюдать, например, при резке ножницами металлических полос или прутков, при пробивании отверстия в заготовках на штампе (рис. 1).

Рассмотрим брус площадью поперечного сечения А, перпендикулярно оси которого приложены две равные и противоположно направленные силы F; линии действия этих сил параллельны и находятся на относительно небольшом расстоянии друг от друга. Для определения поперечной силы Q применим метод сечений (рис. 2). Во всех точках поперечного сечения действуют распределенные силы, равнодействующую которых определим из условия равновесия оставленной части бруса:

• Σ Y = 0 » F – Q = 0,
• откуда поперечная сила Q может быть определена, как:
• Q = F.

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении бруса при сдвиге. Очевидно, что при сдвиге в поперечном сечении возникают только касательные напряжения τ.

1. Предполагаем, что эти касательные напряжения равномерно распределены по сечению, и, следовательно, могут быть вычислены по формуле:
2. τ = Q / А.
3. На основании полученной формулы можно сделать вывод, что форма сечения на величину напряжения при деформации сдвига не влияет.
4. ***

Расчеты на прочность при сдвиге

Условие прочности детали конструкции заключается в том, что наибольшее напряжение, возникающее в ней (рабочее напряжение), не должно превышать допускаемое. Расчетная формула при сдвиге:

τ = Q / А ≤

читается следующим образом: касательное напряжение при сдвиге не должно превышать допускаемое. (при обозначении предельно допустимых напряжений применяют квадратные скобки: или ) По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку.

Деформация сдвига, доведенная до разрушения материала, называется срезом (применительно к металлам) или скалыванием (применительно к неметаллам). Допускаемое напряжение на срез выбирают для пластичных материалов в зависимости от предела текучести.

В машиностроении для штифтов, болтов, шпонок и других деталей, работающих на срез принимают = (0,25….0,35) σт, где σт – предел текучести материала изделия.

При расчетах на срез в случае, если соединение осуществляется несколькими одинаковыми деталями (болтами, заклепками и т. д.), полагают, что все они нагружены одинаково. Расчеты соединений на срез обычно сопровождают проверкой прочности этих соединений на смятие.

***



Для установления параметров, характеризующих деформацию при сдвиге, рассмотрим элемент бруса в виде параллелепипеда abcd, на грани которого действуют только касательные напряжения τ, а противоположную грань параллелепипеда представим жестко защемленной (рис. 3).

Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bc по отношению к сечению, принятому за неподвижное.

Деформация сдвига характеризуется углом γ (гамма) и называется углом сдвига, или относительным сдвигом. Величина bb1, на которую смещается подвижная грань относительно неподвижной, называется абсолютным сдвигом.

Относительный сдвиг γ выражается в радианах.

Напряжения и деформации при сдвиге связаны между собой зависимостью, которая называется закон Гука при сдвиге. Закон Гука при сдвиге справедлив лишь в определенных пределах нагрузок и формулируется так: касательное напряжение прямо пропорционально относительному сдвигу.

Математически закон Гука для деформации сдвига можно записать в виде равенства:

τ = G γ.

Коэффициент пропорциональности G характеризует жесткость материала, т. е. способность сопротивляться упругим деформациям при сдвиге, и называется модулем сдвига или модулем упругости второго рода.

Модуль упругости выражается в паскалях; для различных материалов его величина определена экспериментально и ее можно найти в специальных справочниках. При проведении ответственных расчетов на срез величина модуля упругости для каждого соединения определяется опытным путем, непосредственно перед расчетом, либо берется из справочника с применением увеличенного запаса прочности.

• Следует отметить, что между тремя упругими постоянными (модулями упругости) E, G и ν существует следующая зависимость:
• G = E / .
• Принимая для сталей ν ≈ 0,25, получаем: Gст ≈ 0,4 Ест .
• ***
• Материалы раздела «Сопротивление материалов»:



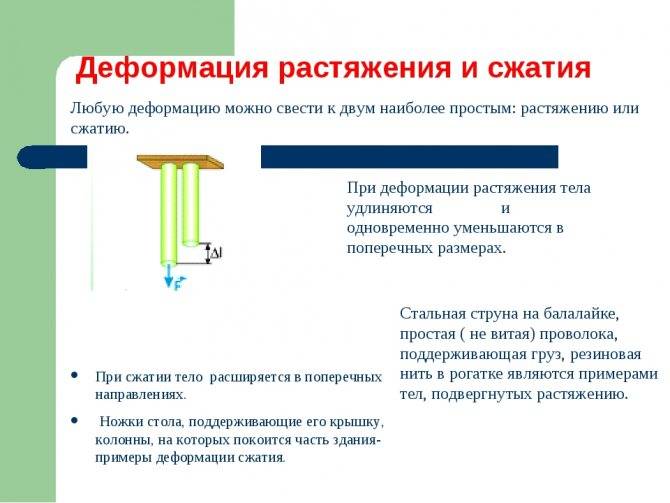
Пластическая и упругая деформация

В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина

Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму

Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.

За счет наличия деформационных способностей все известные материалы обладают набором полезных свойств – пластичностью, хрупкостью, упругостью, прочностью и другими. Исследование этих свойств достаточно важная задача, позволяющая выбрать или изготовить необходимый материал. Кроме того, само по себе наличие деформации и его детектирование часто бывает необходимо для задач приборостроения, для этого применяются специальные датчики называемые экстензометрами или по другому тензометрами.

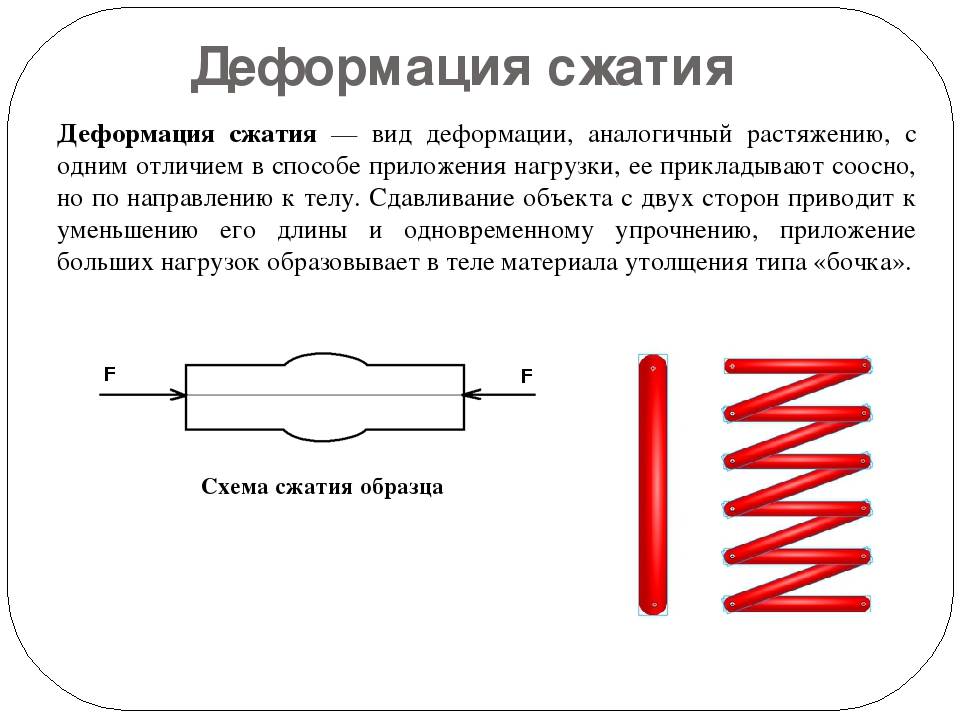
Испытание на сжатие:

Испытание на сжатие – это определение поведения материала при сжимающей нагрузке.

Испытание на сжатие обычно используется для камня и бетона. Испытание на сжатие показывает напряжение и деформацию материала. Экспериментальный результат должен подтвердить теоретические выводы.

Виды компрессионного тестирования: 

• Испытание на изгиб
• Весенний тест
• Испытание на раздавливание

Испытание на сжатие предназначено для определения параметров целостности и безопасности материала путем выдерживания сжимающего напряжения. Также обеспечивается сохранность готовой продукции, комплектующих, изготавливаемого инструмента. Он определяет, подходит ли материал для этой цели и соответствующим образом изготовлен.

Тесты сжатия предоставляют данные для следующих целей:

• Для измерения качества партии
• Чтобы понять последовательность в производстве
• Помочь в процедуре проектирования
• Уменьшить цену материала
• Гарантировать качество по международным стандартам и т. Д.

Напряжение сжатия и растягивающее напряжение | Напряжение сжатия и растягивающее напряжение

	Сжимающее напряжение	Растягивающее напряжение
Результаты	Последствия сжатия материала в результате сдавливания материала.	Результаты растягивающего напряжения при растяжении материала
Толкать или тянуть	В то время как сжимающее напряжение – это давление, оказываемое на тело внешними силами, чтобы изменить его форму и размер.	Напряжение растяжения – это сила, которую тело испытывает от внешних сил, чтобы изменить его форму и размер.
Сжатие или удлинение	Напряжение сжатия создается из-за внешней сжимающей силы	Напряжение растяжения возникает из-за того, что сила растяжения стремится к растяжению.
Приложение на баре	Когда стержень подвергается сжимающему напряжению, деформации сжимающие (отрицательные).	Когда стержень подвергается растягивающему напряжению, деформации растяжения (положительные).

для теплоустойчивых хромистых сталей

12XM, 12MX, 15XM, 15X5M, 15X5M-У:

1. При расчетных температурах ниже 20 °С допускаемые напряжения принимают такими же, как при 20 °С при условии допустимого применения материала при данной температуре.
2. Для промежуточных расчетных температур стенки допускаемое напряжение определяют линейной интерполяцией с округлением результатов до 0,5 МПа в сторону меньшего значения.
3. Допускаемые напряжения, расположенные ниже горизонтальной черты, действительны при ресурсе 105 ч. Для расчетного срока эксплуатации до 2*105 ч допускаемое напряжение, расположенное ниже горизонтальной черты, умножают на коэффициент 0,85.

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Основные понятия

Под изгибом детали понимают естественное или искусственное изменение формы. Этот процесс разделяется на две категории – плоский или косой. В первом случае ось детали сохраняет своё первоначальное положение, во втором происходит её изменение в горизонтальной или вертикальной плоскости.

Основным теоретическим положением, определяющим физические процессы, протекающие в результате изгиба, является закон Гука. Согласно ему величина деформации (изгиба), пропорциональна приложенной к этому телу силе. Для каждого из видов деформации разработан индивидуальный расчёт действующих характеристик.

Оценка степени влияния действующих факторов на деформацию осуществляется с помощью следующих показателей:

• площади поверхности подверженной деформации;
• длины детали;
• силы, воздействующие на конструкцию;
• модуль упругости (его абсолютный показатель);
• величина и характер изменения модуля длины в результате упругой деформации.

Одним из важных параметров считается потенциальная энергия деформации при изгибе. На основании этих параметров производят определение модуля Юнга. С его помощью рассчитывают скорость распространения продольной волны. Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а сам объект способен восстановить первоначальную форму после снятия нагрузки, называется пределом упругости. При превышении допустимого значения этого параметра тело начнёт разрушаться. Этот предел называется прочностью. При оценке прочностных показателей применяют следующие предположения:

1. О постоянстве нормальных напряжений. Она определяет постоянство расстояний при возникновении напряжений изгиба.
2. Плоскости сечений. Оно называется гипотезой Бернулли. Сечения детали в спокойном положении находятся в плоском состоянии. После деформации они сохраняют первоначальную форму, но разворачиваются относительно некоторой линии. Она называется нейтральной осью.
3. Отсутствие давлений на боковые поверхности. Считается, что соседние волокна не оказывают давления друг на друга.

Перечисленные гипотезы позволяют оценить деформации сдвига и характер изгиба каждого слоя исследуемой детали. Это происходит в результате воздействия различных сил. Нагрузки вызывают деформацию изгиба в различных плоскостях. Они подразделяются на две категории:

• характеру воздействия (статические или динамические);
• степени воздействия (массовые или объёмные);
• поверхности (сосредоточенные, воздействуют на отдельные элементы поверхности и распределёнными – на всю поверхность).

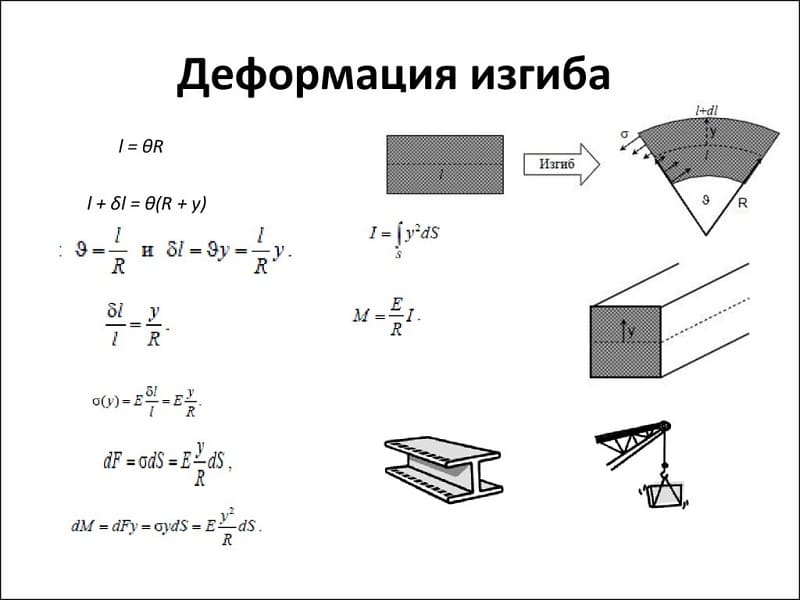
К статическим относятся нагрузки, у которых место приложения и направления сил не меняется или изменяются медленно в течение определённого промежутка времени. К таким нагрузкам относится сила тяжести. В этом случае можно принять утверждение, что элементы физического объекта находятся в состоянии равновесия. У динамических нагрузок эти параметры меняются достаточно быстро или носят импульсивный характер. К ним относятся ударные нагрузки при забивании свай, обработке металла ковкой, воздействие неровностей дороги на колесо.

При сосредоточенной статической нагрузке на отдельный участок поверхности бруса происходит его деформация в сторону по направлению сил взаимодействия. Для расчёта параметров характеризующих основные показатели состояния деформированного тела применяют дифференциальные уравнения, которые позволяют выявить существующие функциональные связи. По деформации изгиба с помощью модуля Юнга можно вычислить прочность исследуемого элемента конструкции (балки, бруса, подвесной опоры и т. д.). На основании полученных областей решения можно построить графическое изображение силы упругости, которое наглядно показывает, что происходит с различными участками деформированной детали. Для каждой детали в зависимости от её геометрических размеров, материала изготовления и величины приложенных сил выведена своя формула.

Для наглядности восприятия характера протекающих процессов использует метод нанесения эпюр на поверхность объекта. Эта операция называется топология. Основной идеей является проецирование линий нагрузки на соответствующую плоскость (горизонтальную, фронтальную или профильную). В современных методах топологии применяют фрактальную геометрию.

Напряжения при растяжении-сжатии.

Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня. Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.

Прочность на сжатие:

Это способность материала противостоять сжатию, возникающему из-за сжимающего напряжения. Некоторые материалы могут выдерживать только одно растяжение, некоторые материалы могут выдерживать только сжатие, а некоторые материалы могут выдерживать как растяжение, так и сжатие. Предел прочности на сжатие – это величина, полученная при полном разрушении материала. Испытание на сжатие проводится так же, как испытание на растяжение. Единственная разница в том, что используемая нагрузка – это сжимающая нагрузка.

Прочность на сжатие выше у камня и бетона.

Кредит изображения: Железный стержень at en.wikipedia, Инженерное напряжение-деформация, CC BY-SA 3.0

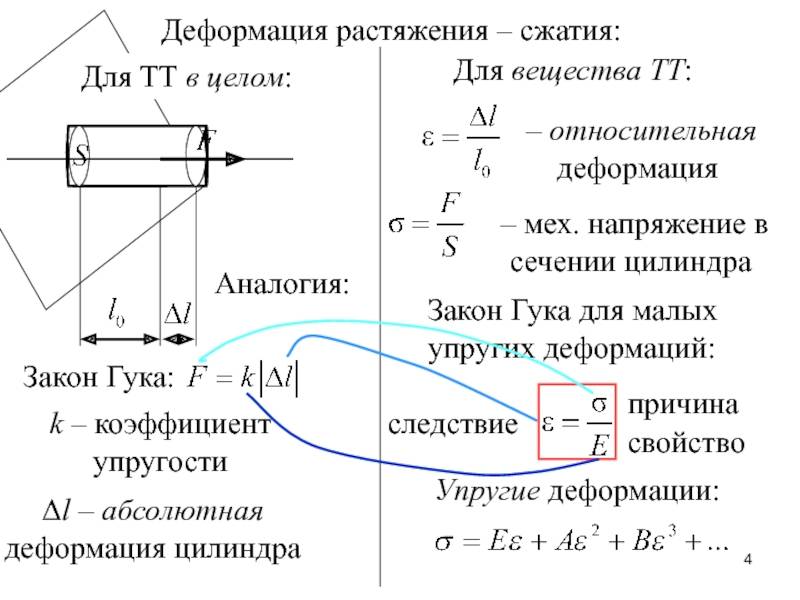
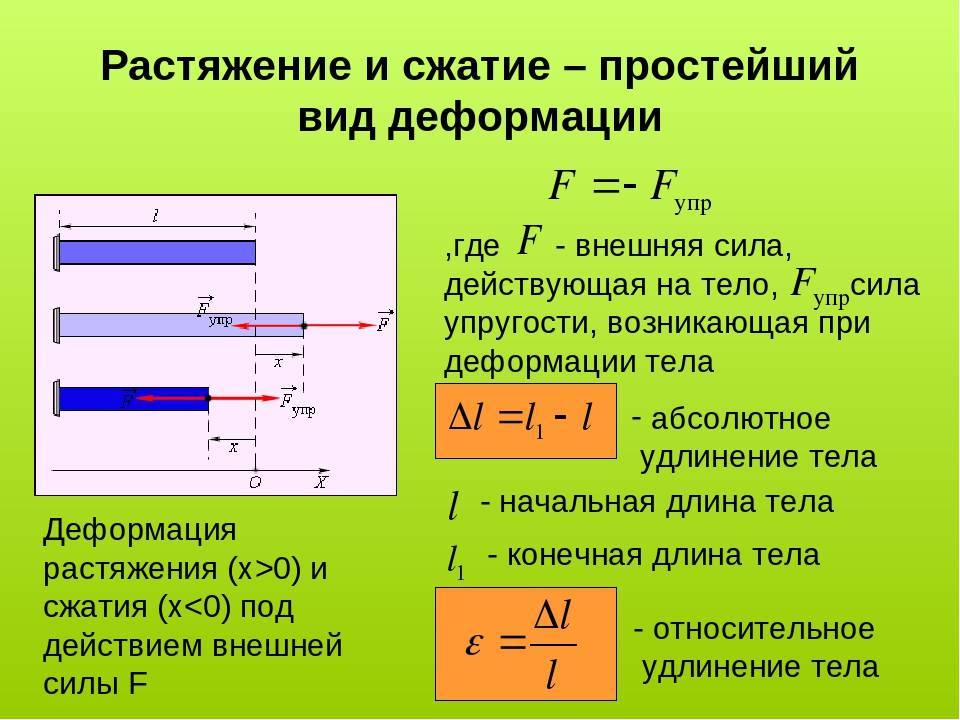
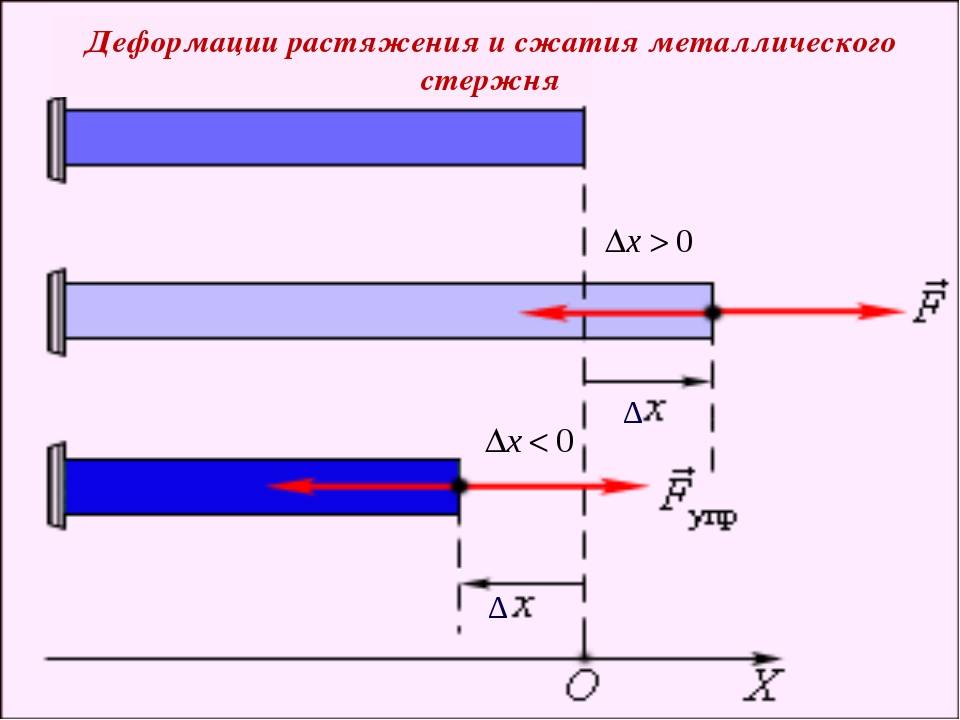
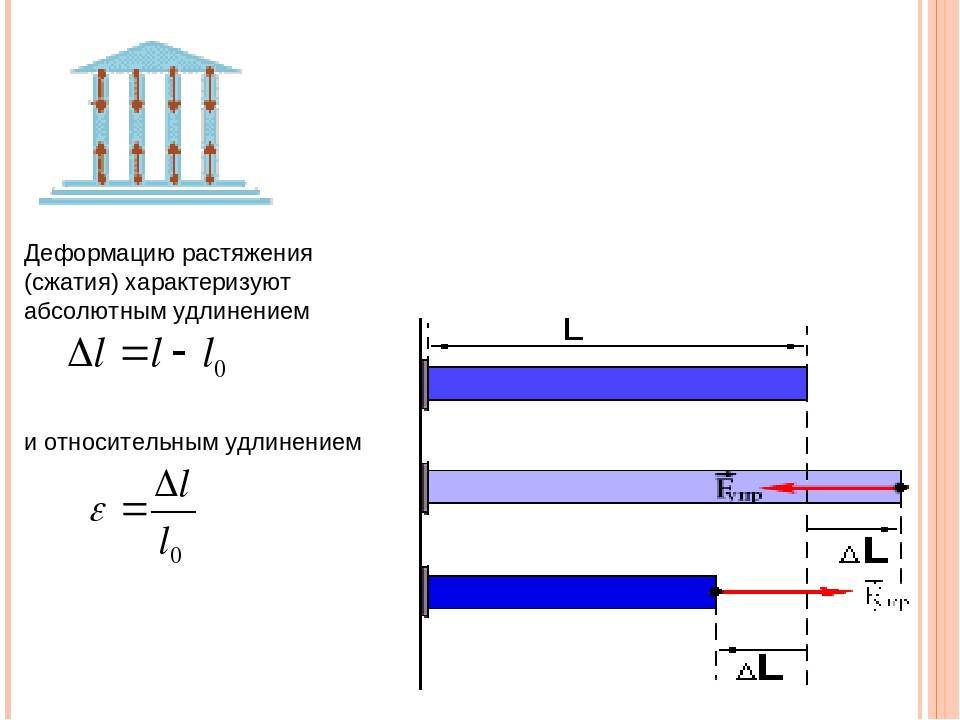
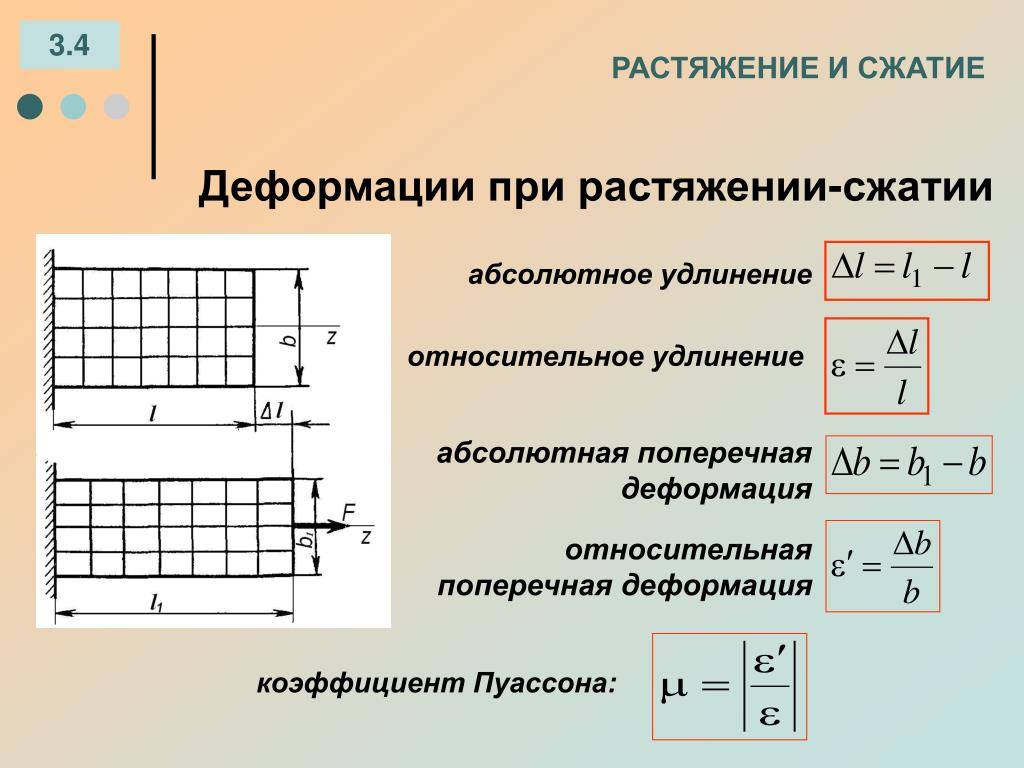
Деформации при растяжении сжатии

При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.

Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.

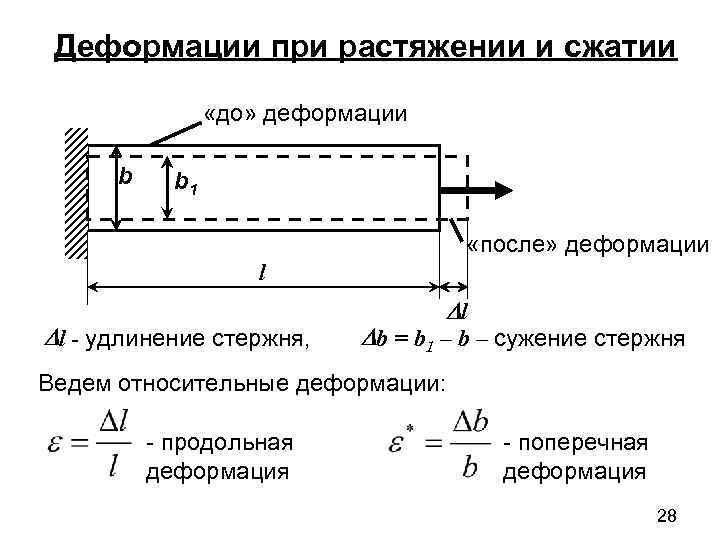
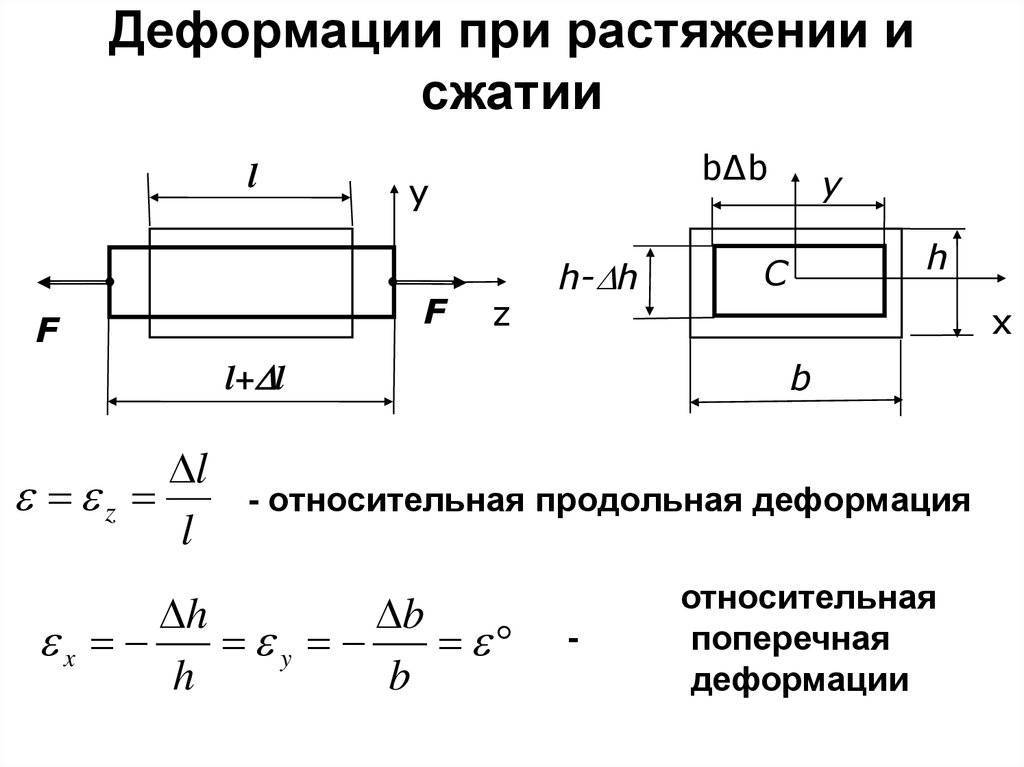
Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.

Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:

F=kx

В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.

для теплоустойчивых хромистых сталей

12XM, 12MX, 15XM, 15X5M, 15X5M-У:

1. При расчетных температурах ниже 20 °С допускаемые напряжения принимают такими же, как при 20 °С при условии допустимого применения материала при данной температуре.
2. Для промежуточных расчетных температур стенки допускаемое напряжение определяют линейной интерполяцией с округлением результатов до 0,5 МПа в сторону меньшего значения.
3. Допускаемые напряжения, расположенные ниже горизонтальной черты, действительны при ресурсе 105 ч. Для расчетного срока эксплуатации до 2*105 ч допускаемое напряжение, расположенное ниже горизонтальной черты, умножают на коэффициент 0,85.

для титана и его сплавов

ВТ1-0, ОТ4-0, АТ3, ВТ1-00:

1. При расчетных температурах ниже 20 °С допускаемые напряжения принимают такими же, как при 20 °С, при условии допустимости применения материала при данной температуре.
2. Для поковок и прутков допускаемые напряжения умножаются на 0,8.

II. Определения и обозначения:

Re/20 — минимальное значение предела текучести при температуре 20 °C, МПа; Rр0,2/20 — минимальное значение условного предела текучести при остаточном удлинении 0,2% при температуре 20 °С, МПа. допускаемое напряжение — наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы. Значение допускаемого напряжения устанавливается путем деления предела прочности, предела текучести и пр. на величину, большую единицы, называемую коэффициентом запаса. расчетная температура — температура стенки оборудования или трубопровода, равная максимальному среднеарифметическому значению температур на его наружной и внутренней поверхностях в одном сечении при нормальных условиях эксплуатации (для частей корпусов ядерных реакторов расчетная температура определяется с учетом внутренних тепловыделений как среднеинтегральное значение распределения температур по толщине стенки корпуса (ПНАЭ Г-7-002-86, п.2.2; ПНАЭ Г-7-008-89, прил.1).

Расчетная температура

• ,п.5.1. Расчетную температуру используют для определения физико-механических характеристик материала и допускаемых напряжений, а также при расчете на прочность с учетом температурных воздействий.
• ,п.5.2. Расчетную температуру определяют на основании теплотехнических расчетов или результатов испытаний, или опыта эксплуатации аналогичных сосудов.
• За расчетную температуру стенки сосуда или аппарата принимают наибольшую температуру стенки. При температуре ниже 20 °С за расчетную температуру при определении допускаемых напряжений принимают температуру 20 °С.
• ,п.5.3. Если невозможно провести тепловые расчеты или измерения и если во время эксплуатации температура стенки повышается до температуры среды, соприкасающейся со стенкой, то за расчетную температуру следует принимать наибольшую температуру среды, но не ниже 20 °С.
• При обогреве открытым пламенем, отработанными газами или электронагревателями расчетную температуру принимают равной температуре среды, увеличенной на 20 °С при закрытом обогреве и на 50 °С при прямом обогреве, если нет более точных данных.
• ,п.5.4. Если сосуд или аппарат эксплуатируются при нескольких различных режимах нагружения или разные элементы аппарата работают в разных условиях, для каждого режима можно определить свою расчетную температуру (ГОСТ-52857.1-2007, п.5).

III. Примечание:

Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.

для титана и его сплавов

ВТ1-0, ОТ4-0, АТ3, ВТ1-00:

1. При расчетных температурах ниже 20 °С допускаемые напряжения принимают такими же, как при 20 °С, при условии допустимости применения материала при данной температуре.
2. Для поковок и прутков допускаемые напряжения умножаются на 0,8.

II. Определения и обозначения:

Re/20 — минимальное значение предела текучести при температуре 20 °C, МПа; Rр0,2/20 — минимальное значение условного предела текучести при остаточном удлинении 0,2% при температуре 20 °С, МПа. допускаемое напряжение — наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы. Значение допускаемого напряжения устанавливается путем деления предела прочности, предела текучести и пр. на величину, большую единицы, называемую коэффициентом запаса. расчетная температура — температура стенки оборудования или трубопровода, равная максимальному среднеарифметическому значению температур на его наружной и внутренней поверхностях в одном сечении при нормальных условиях эксплуатации (для частей корпусов ядерных реакторов расчетная температура определяется с учетом внутренних тепловыделений как среднеинтегральное значение распределения температур по толщине стенки корпуса (ПНАЭ Г-7-002-86, п.2.2; ПНАЭ Г-7-008-89, прил.1).

Расчетная температура

• ,п.5.1. Расчетную температуру используют для определения физико-механических характеристик материала и допускаемых напряжений, а также при расчете на прочность с учетом температурных воздействий.
• ,п.5.2. Расчетную температуру определяют на основании теплотехнических расчетов или результатов испытаний, или опыта эксплуатации аналогичных сосудов.
• За расчетную температуру стенки сосуда или аппарата принимают наибольшую температуру стенки. При температуре ниже 20 °С за расчетную температуру при определении допускаемых напряжений принимают температуру 20 °С.
• ,п.5.3. Если невозможно провести тепловые расчеты или измерения и если во время эксплуатации температура стенки повышается до температуры среды, соприкасающейся со стенкой, то за расчетную температуру следует принимать наибольшую температуру среды, но не ниже 20 °С.
• При обогреве открытым пламенем, отработанными газами или электронагревателями расчетную температуру принимают равной температуре среды, увеличенной на 20 °С при закрытом обогреве и на 50 °С при прямом обогреве, если нет более точных данных.
• ,п.5.4. Если сосуд или аппарат эксплуатируются при нескольких различных режимах нагружения или разные элементы аппарата работают в разных условиях, для каждого режима можно определить свою расчетную температуру (ГОСТ-52857.1-2007, п.5).

III. Примечание:

Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.