Чертежи зубчатого колеса

Чертеж – коническое зубчатое колесо

Чертеж – коническое зубчатое колесо

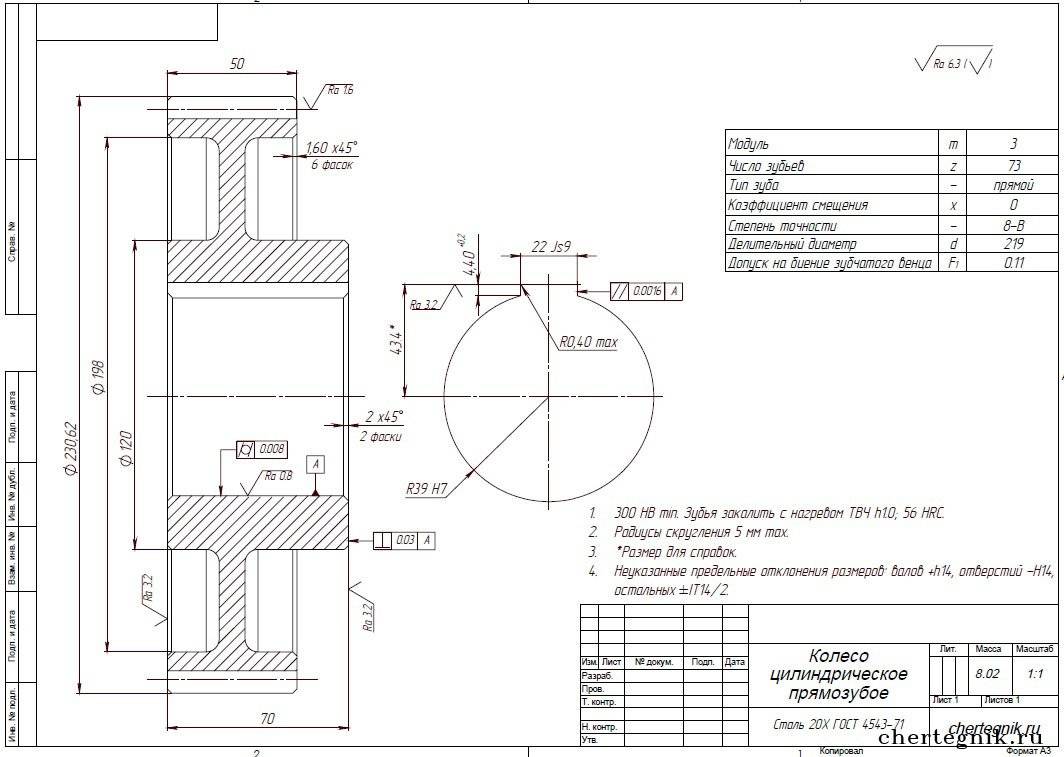
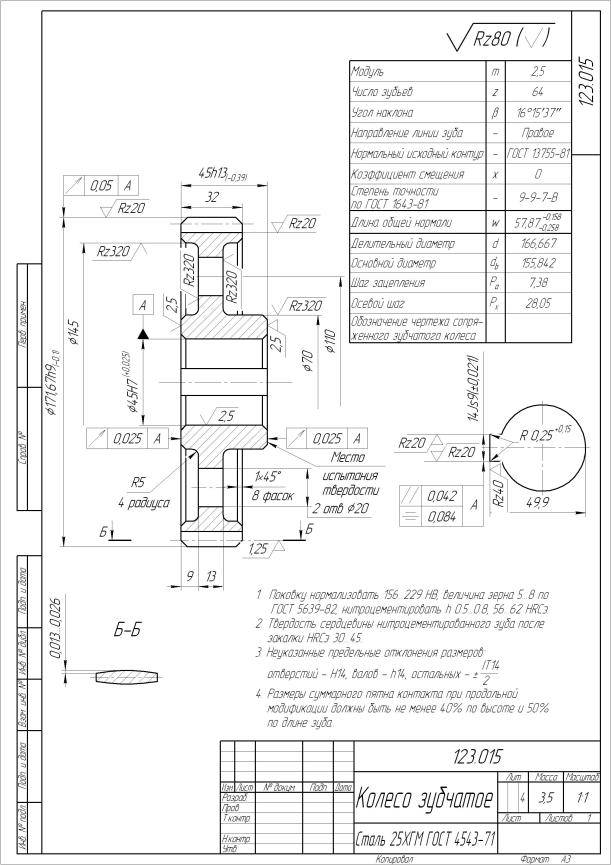
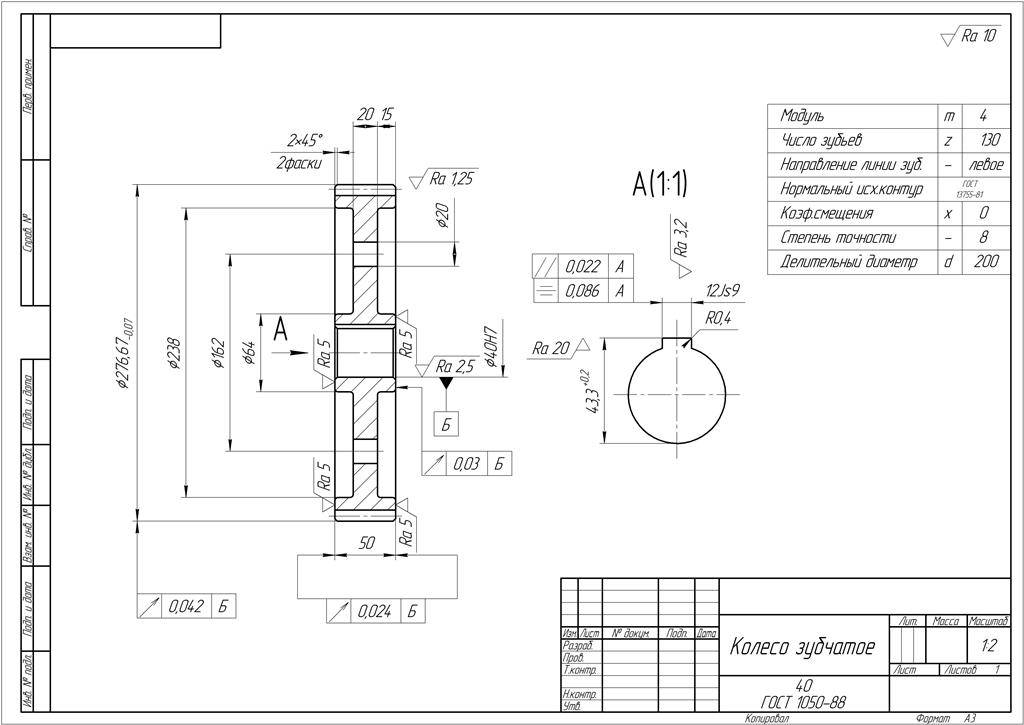
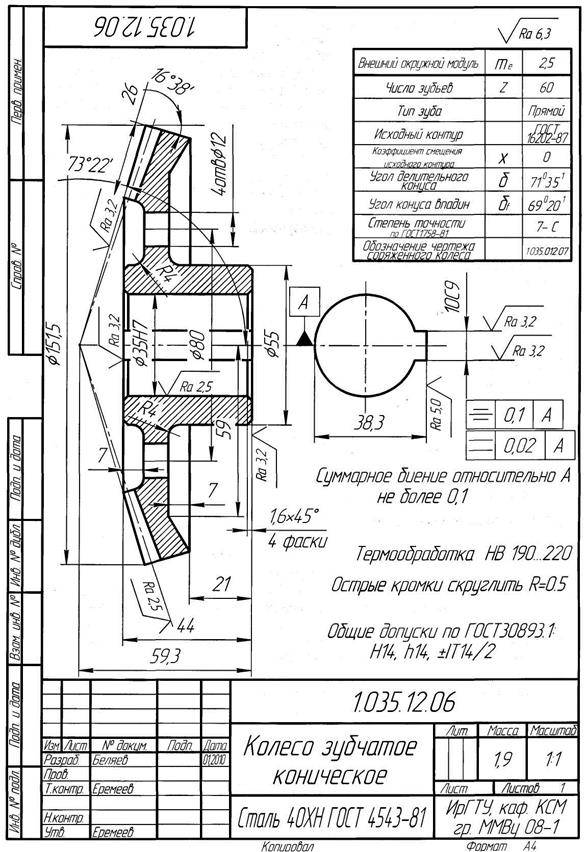
Чертежи конических зубчатых колес с прямолинейным профилем исходного контура выполняются по ГОСТ 2.405 – 75 в части указания параметров зубчатого венца и по другим стандартам ЕСКД.
 

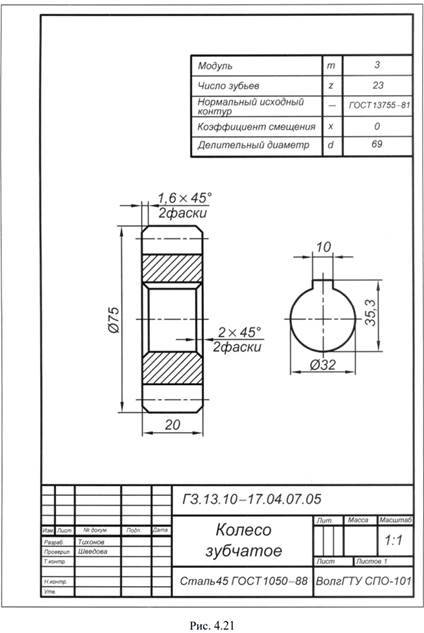
Чертеж конического зубчатого колеса ( см. рис. 21) начинают тонкими линиями с проведения горизонтальной оси.
 

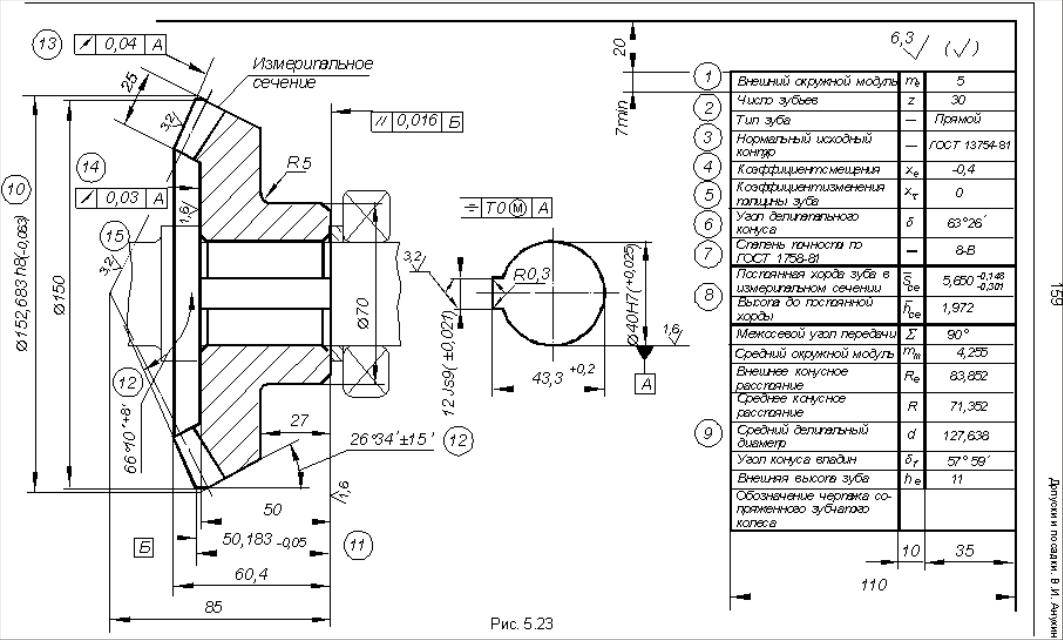
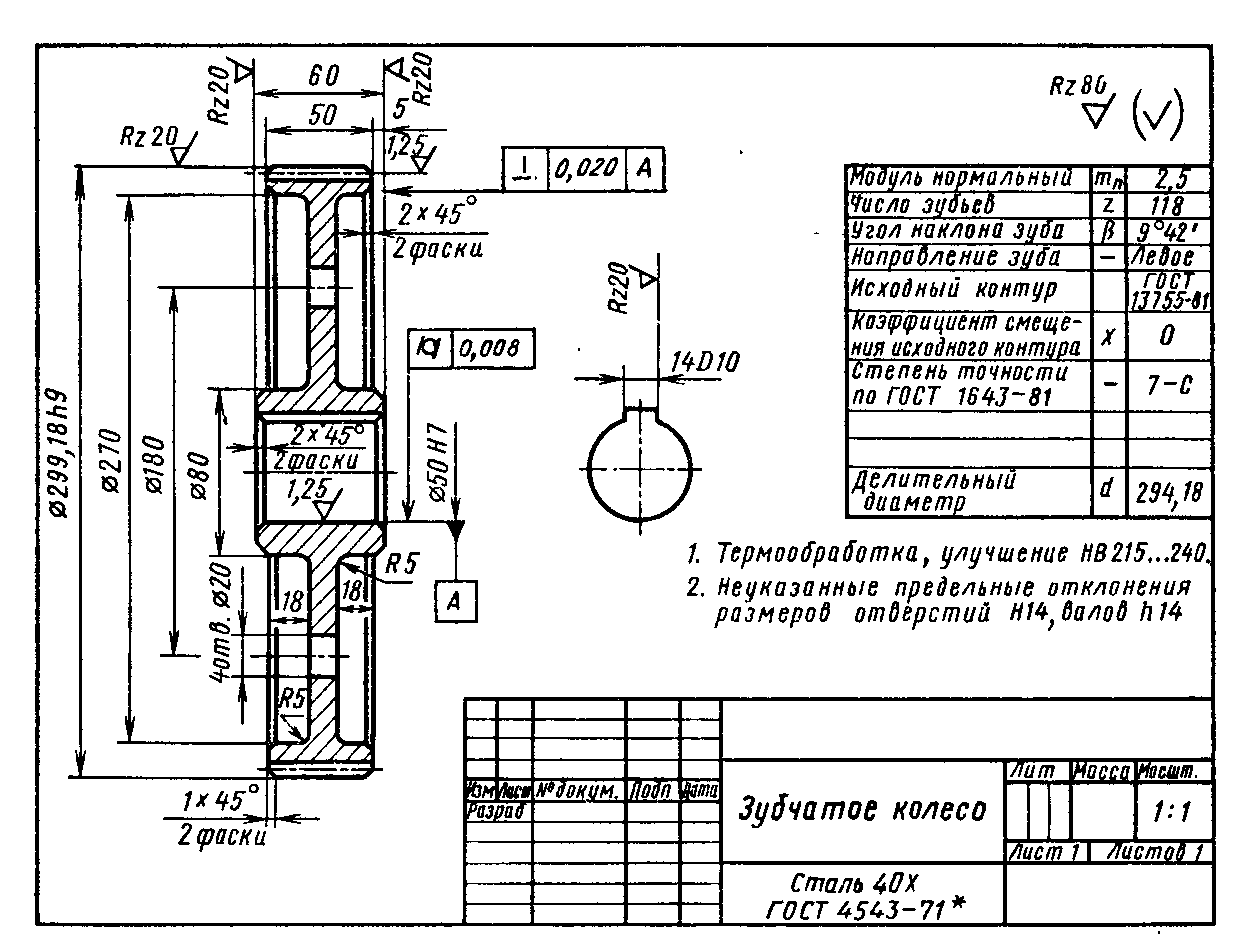
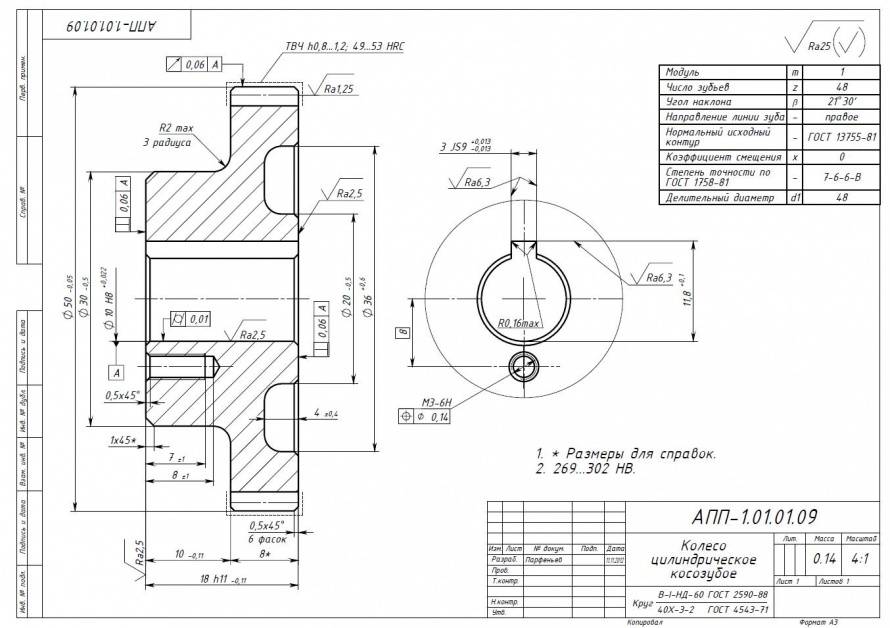
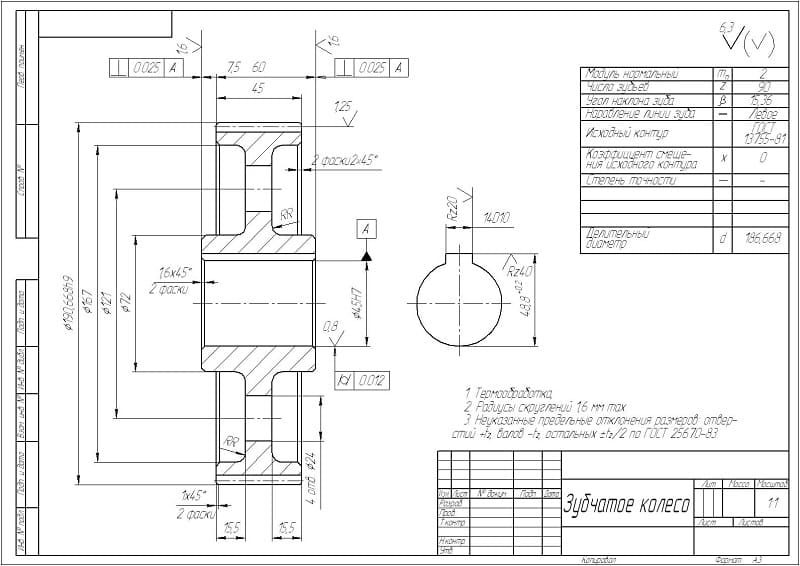
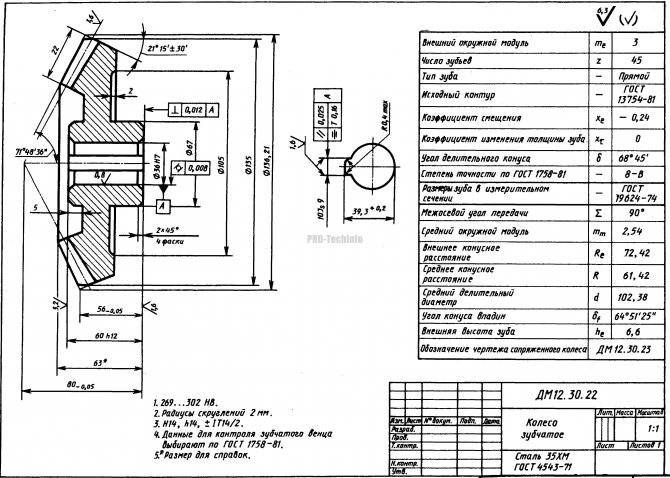
На чертежах конических зубчатых колес кроме размеров, определяющих форму и габариты детали, приводят размеры венца ( рис. 22.26, а, б): внешние диаметры dae и dae; угол 8а конуса вершин зубьев; угол 8 делительного конуса; угол ( 90 – 5) внешнего дополнительного конуса. Звездочкой обозначены размеры для справок.
 

На чертеже конического зубчатого колеса обозначают внешний диаметр вершин зубьев до притупления кромки dae и внешний диалгетр вершин зубьев после притупления кромки d ae, поскольку конус вершин зубьев и внешний делительный дополнительный конус на поверхности колеса не пересекаются. Наличие этой поверхности обусловлено тем, что часть цилиндрической поверхности заготовки длиной 1 х сохраняется при обработке по конусу вершин зубьев и внешнему делительному дополнительному конусу. Величину 1 х для мелкомодульных конических зубчатых колес принимают равной 0 1 мм.
 

На чертеже конического зубчатого колеса помещают таблицу параметров зубчатого венца, которая должна состоять из трех частей, отделенных друг от друга сплошными основными линиями: первая часть – основные данные; вторая – данные для контроля; третья – справочные данные.
 

На чертеже конического зубчатого колеса на изображении или в технических требованиях допускается приводить данные о форме, расположении и поведении зоны касания.
 

В какой последовательности выполняется чертеж конического зубчатого колеса.
 

В какой последовательности выполняют чертеж конического зубчатого колеса. Какие данные указывают на изображении конического зубчатого колеса.
 

Примеры простановки размеров на чертежах конических зубчатых колес приведены на фиг. Кроме основных значений, в штампе нужно указать еще и межосевой угол.
 

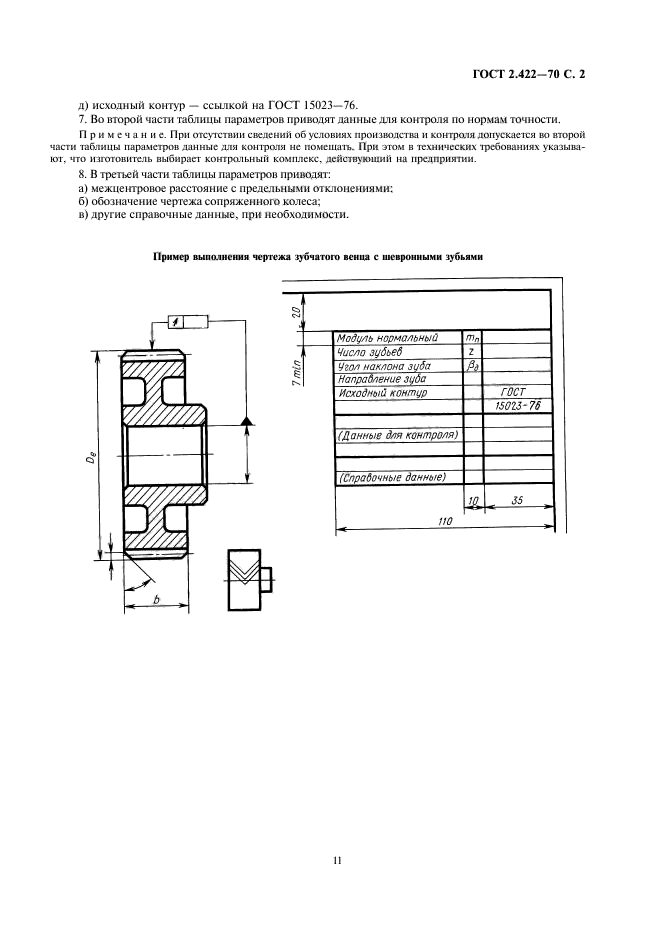
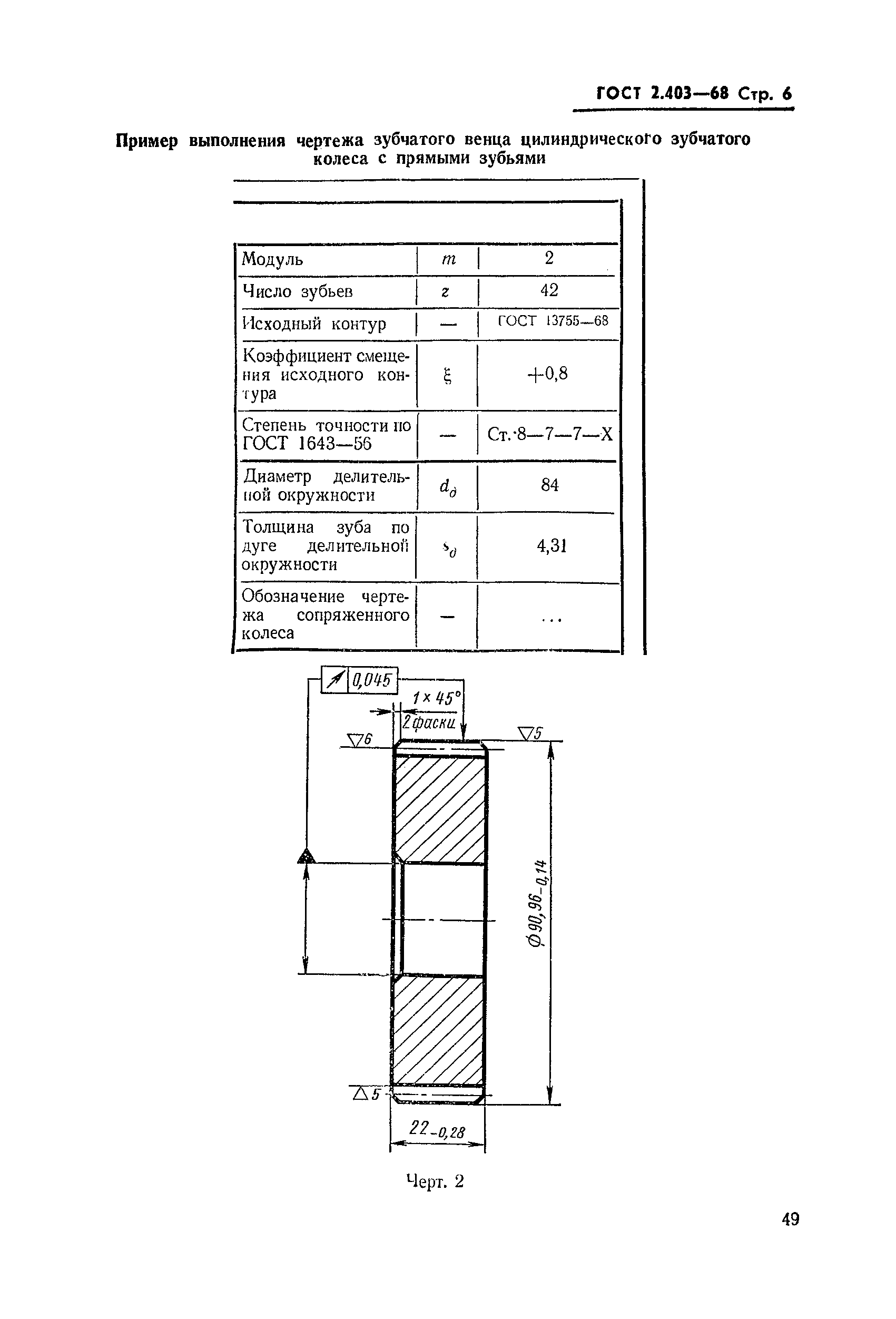
Пример указания параметров зубчатого венца на чертеже прямозубого конического зубчатого колеса со стандартным исходным контуром приведен на рис. 5.5. На чертеже помещается таблица параметров зубчатого венца, состоящая из трех частей, отделяемых сплошными основными линиями.
 

На рис. 16.44 приведен в качестве примера чертеж конического зубчатого колеса, из которого видно также и содержание таблицы для нарезания зубьев.
 

На рис. 268, в, г, д показана последовательность построения чертежа конического зубчатого колеса. Начинают с вычерчивания двух делительных конусов, имеющих общую образующую, нижний конус принадлежит колесу, верхний – сопряженной с ним шестерне.
 

Размеры толщины зуба s и высоты его головки hx по зубомеру ( рис. 149, а) определяют, зная модуль и число зубьев, используя соответствующие справочники, и проставляют в таблице параметров, обычно на чертежах конических зубчатых колес.
 

Страницы:  

   1

   2

Цилиндрические зубчатые колеса(шестерни):

Цилиндрические зубчатые колеса используются в передачах, где оси валов располагаются параллельно относительно друг друга. При этом они могут располагаться как горизонтально, так и вертикально.

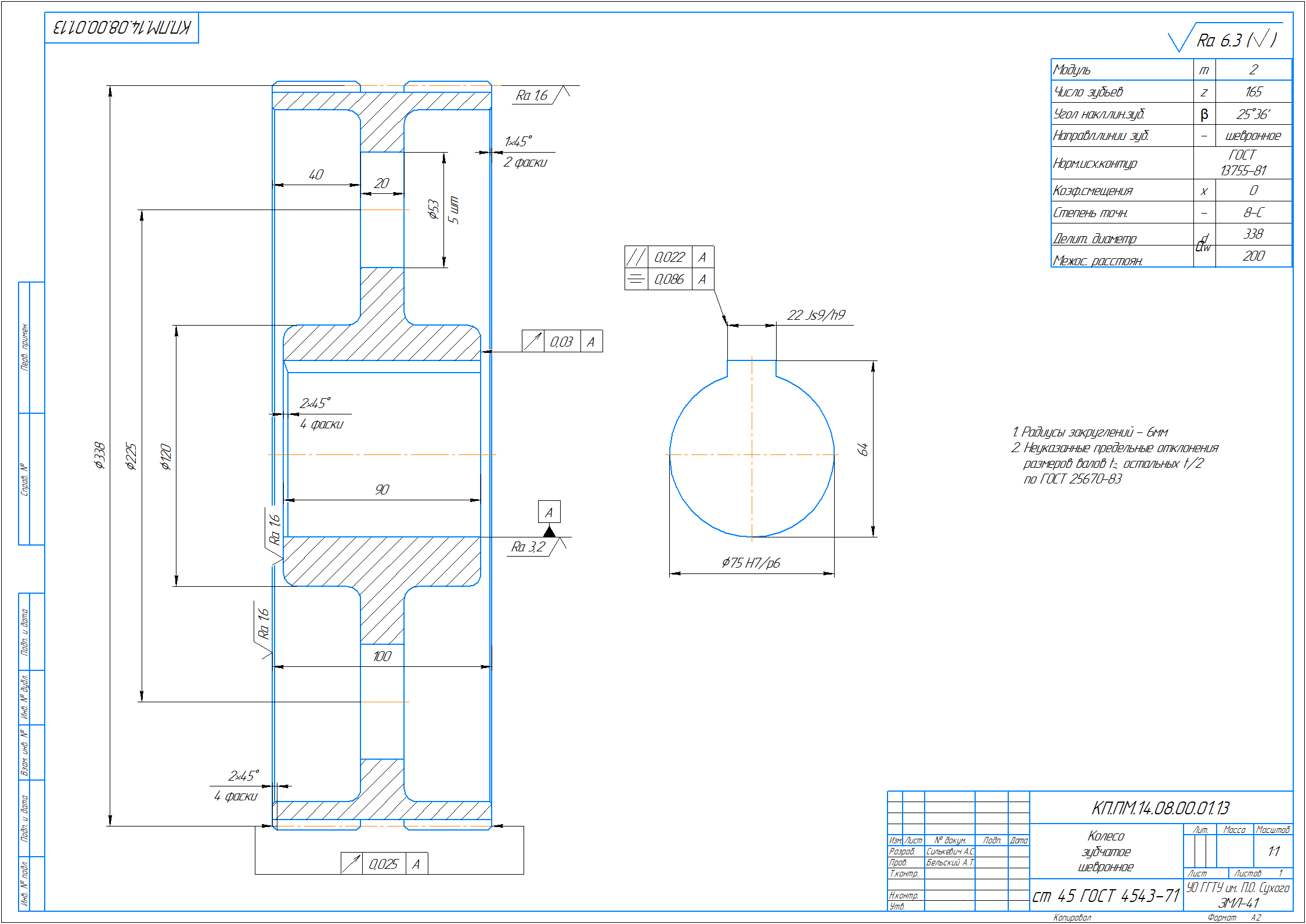
В зависимости от формы продольной линии зуба зубчатые колеса бывают: прямозубые, косозубые и шевронные.

Рис. 1. Цилиндрические зубчатые колеса: прямозубые, косозубые и шевронные

Прямозубое колесо. Этот вид шестерен ввиду своей простой конструкции является наиболее внедряемым в различных системах. В таком виде зубья шестерен располагаются в плоскости, которая перпендикулярна оси вращения. В отличии от косозубых и шевронных колес у данного вида предельный крутящий момент ниже.

Косозубое колесо. Зубья для данного вида колес выполняются под определенным углом к оси вращения шестерен, а по форме образуют часть винтовой линии. По сравнению с прямозубым колесом при работе зубьев данного вида зацепление зубьев происходит плавнее, а за счет увеличенной площади контакта предельный крутящий момент выше. Но для работы колес с косым зубом приходится применять упорные подшипники, так как возникает механическая сила, направленная вдоль оси. В основном косозубые колёса используются там, где нужны передачи большого крутящего момента на высоких скоростях.

Шевронное колесо. Этот вид имеет зубья, которые выполнены в форме буквы V на плоскости вращения колеса. Главной особенностью шевронных колес является то, что силы на осях обеих половин компенсируются, вследствие чего отпадает необходимость в использовании упорных подшипников. Различают шевронное и многошевронное цилиндрическое зубчатое колесо, состоящее соответственно из двух и более полушевронов, а также шевронное цилиндрическое зубчатое колесо со сплошным венцом и разделенными полушевронами.

В отдельные виды выделяются: цилиндрическое колесо с круговыми зубьями, цилиндрическое колесо со смещением (без смещения), циклоидальное, эвольвентное и цевочное цилиндрическое колеса.

Колесо с круговыми зубьями. Передачу с такими колесами называют передачей Новикова. При такой передаче контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс. Зубья данного вида колеса выполнены в виде полукруга, радиус которого подбирается под нужные требования. Колеса с круговыми зубьями в сравнении с косозубыми обладают более высокой нагрузочной способностью зацепления, высокой плавностью и бесшумностью работы, но при тех же условиях работы у них снижен КПД и ресурс работы, что не позволяет их применять широко.

Колесо со смещением либо без смещения. Это зубчатое колесо, зубья которого образованы при номинальном положении исходной производящей рейки, характеризуемом отсутствием касания (касанием) делительных поверхностей исходной производящей рейки и обрабатываемого зубчатого колеса.

Циклоидальное колесо. В данном виде профили зубьев шестерни выполнены по циклоидальной кривой. Однако при таком способе зацепления шестерен имеется большой недобор чувствительности из-за изменения расстояния между осями. Циклоидальное колесо применяется в основном в приборостроении. Колесо сложно в изготовлении, поскольку при его создании требуется использование очень многих специальных зуборезных инструментов.

Цевочное колесо. В данном случае зубья одного из колес имеют вид пальцев в форме цилиндра. Такой вид шестерен образовался на базе циклоидального колеса и получил более широкое применение как в машиностроении, так и в приборостроении.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

• для отлитых зубцов: sв=πm-1,53m=1,61m:
• для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Силы, действующие в зацеплении шестерен

Прямозубые цилиндрические шестерни

Нормальная сила, действующая по линии зацепления, разлагается на две составляющие силы:
P = P _ncosα — окружное усилие;
R = P _nsinα — радиальное усилие

На валы действуют те же силы, что и на зубья шестерен, и, кроме того, еще крутящий момент:

Косозубые цилиндрические шестерни

Здесь, вследствие наклона зубьев к образующей, дополнительно возникает еще осевое усилие
окружное усилие

радиальное усилие:
осевое усилие:
нормальное усилие:

Силы P, R, A необходимо определить для расчета валов и подшипников, сила P _n необходима для расчета зубьев шестерен на прочность. Силу A можно уравновесить, применив сдвоенные косозубые шестерни с разнонаправленными спиралями зубьев или шевронные

Конические прямозубые шестерни

Окружное усилие

Осевое усилие для шестерни или радиальное для колеса: A_ш = R_к = R sinγ_ш = P tgα sinγ_ш
Радиальное усилие для шестерни или осевое для колеса: R_ш = A_к = R cosγ_ш = P tgα cosγ_ш
Нормальное усилие:

Силы Р, A_ш, R_ш — для расчета валов и подшипников, cила Р_n — для расчета зубьев на прочность;
d_э, Z_э — диаметры и числа зубьев эквивалентных цилиндрических колес

Воображаемые эквивалентные цилиндрические колеса строятся в плоскости мгновенного зацепления основных конических колес так, что оси тех и других совпадают. Работают эти колеса точно так же, как и основные конические, поэтому такое построение удобно использовать для выяснения действующих сил и напряжений в конических колесах

Дефекты шестерен

Закрытыми называются передачи, заключенные в пыленепроницаемый закрытый корпус, с организованной смазкой.
Открытыми называются передачи, не защищенные от пыли, с нерегулярной смазкой

Износ поверхностей зубьев — очень значительный в открытых передачах и небольшой в закрытых. Меры борьбы с износом — повышение поверхностной твердости зубьев

Питинг — поверхностное выкрашивание зубьев в зоне полосной линии. Возникает вследствие усталости поверхностного слоя зубьев в результате высоких контактных напряжений. Питинг начинается с образования усталостных микротрещин, которые под влиянием циклических нагрузок постепенно развиваются, чему способствует высокое давление масла в зоне контакта зубьев. В открытых передачах питинг обычно не возникает, так как микротрещины изнашиваются раньше, чем успеют развиться.
Меры борьбы с питингом заключаются в повышении жесткости корпусов, валов и опор и точности их изготовления с целью увеличения площадок контакта зубьев

Усталостная изгибная поломка зубьев.
Меры борьбы — увеличение модуля или улучшение качества материала и термообработки

Задиры поверхностей зубьев могут иметь место в тихоходных сильно нагруженных передачах.
Меры борьбы — применение противозадирных смазок, содержащих животные жиры и графит

Коническое зубчатое колесо чертеж, зацепление

Конические зубчатые колёса

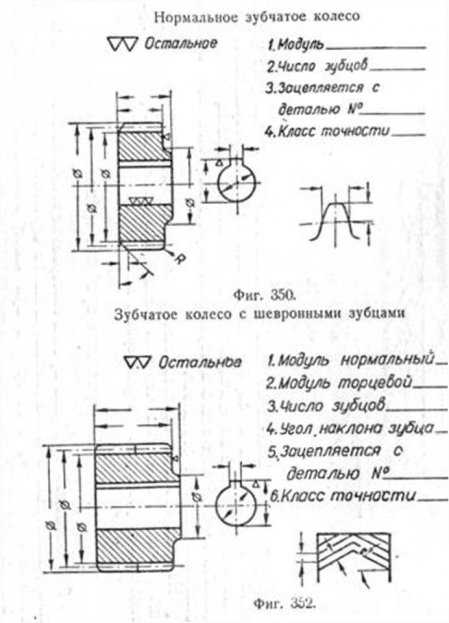
При изготовлении чертежа конического зубчатого колеса с натуры, по аналогии с цилиндрическими колёсами, измеряют наружный диаметр окружности выступов De, затем определяют модуль m и угол внешнего конуса по выступам зубцов (фиг. 363).

Для этого ставят зубчатое колесо торцом ступицы на разметочную плиту и измеряют высоту зубца h по наружному его торцу. Отклады­вают от окружности выступов по торцу зубца размер, равный h/2.2, и

наносят рейсмасом на всех зубцах риску. Риска пройдёт по начальному диаметру колеса d. Измерив d и поделив его на число зубцов z, определяют модуль m. Полученный модуль может несколько отличаться от стандартного вследствие неточности измерений, и поэтому его округ­ляют до ближайшего стандартного значения модуля. Затем производят вычисление и обмер всех элементов колеса. Диаметр начальной окруж­ности определяют по формуле d = mz. Если известно передаточное число зубчатой пары, т. е. отношение числа зубцов большого колеса z₂ к числу зубцов малого z₁ то половина угла при вершине начального конуса ?₂ большого колеса определится (при угле между осями валов 90°) по формуле

tg?₂=z₂/z₁ = i

где i —передаточное число.

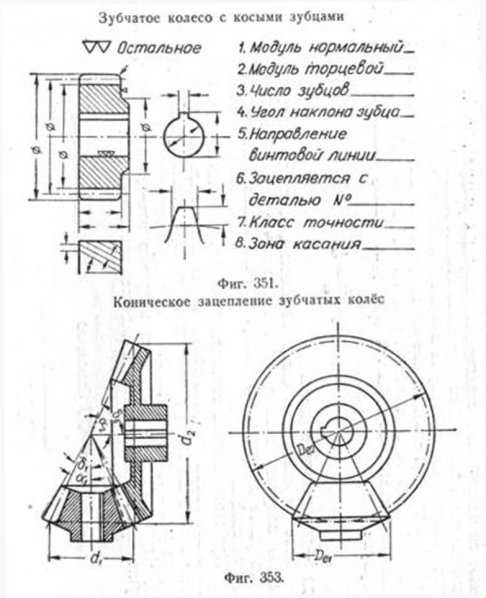
Если передаточное число неизвестно, то угол начального конуса можно получить измерением при помощи угломера, использовав для этого ранее проведённую риску. Так же может быть измерен и угол конуса впадин.

При вычерчивании конического зацепления необходимо, чтобы: вер­шины начальных конусов обоих колёс находились на пересечении их осей; в этой же точке пересекались линии, соответствующие начальным окружностям зубчатых колёс.

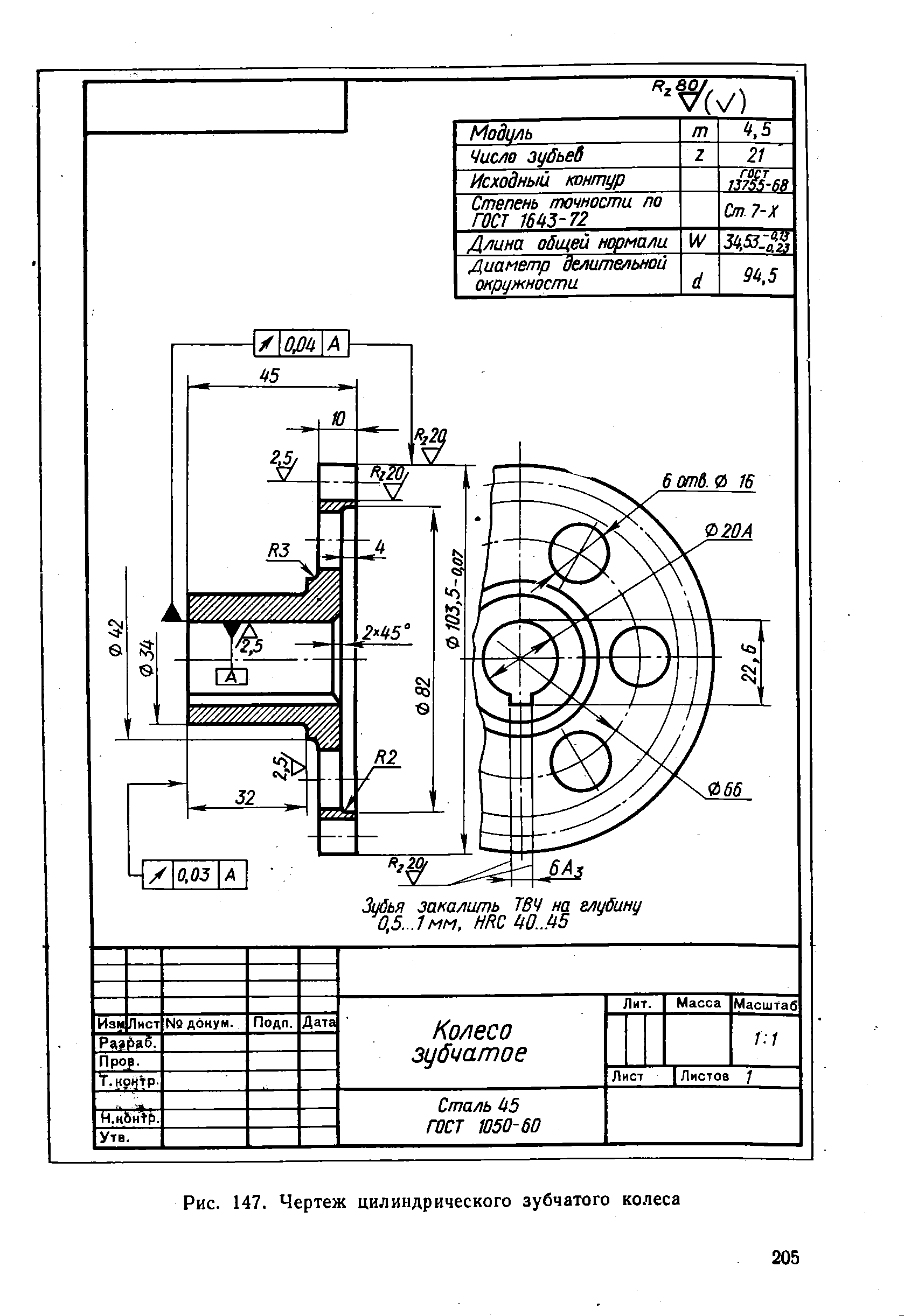
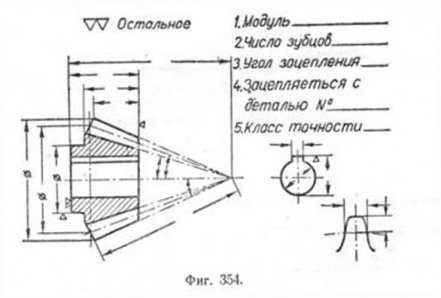
Чертёж конического колеса и пример нанесения размеров, конст­руктивных и технологических надписей показан на фиг. 354.

9.5. Выполнение чертежа детали, имеющей форму тела вращения

Детали, имеющие форму тела вращения, в подавляющем большинстве (50-55% из числа оригинальных деталей) встречаются в машиностроении, т.к. вращательное движение – самый распространённый вид движения элементов существующих механизмов. Кроме того, такие детали технологичны. К ним относятся валы, втулки, диски и т.п. обработка таких деталей производится на токарных станках, где ось вращения расположена горизонтально.

Поэтому детали, имеющие форму тела вращения, располагают на чертежах так, чтобы ось вращения была параллельна основной надпись чертежа (штампу). Торец детали, принятый за технологическую базу для обработки, желательно располагать справа, т.е. так, как он будет расположен при обработке на станке. На рабочем чертеже втулки (Рисунок  9.9) показано выполнение детали, являющейся поверхностью вращения. Наружные и внутренние поверхности детали ограничены поверхностями вращения и плоскостями. Другим примером может быть деталь «Вал» (Рисунок 9.10), ограниченная соосными поверхностями вращения. Осевая линия параллельна основной надписи. Размеры проставлены комбинированным способом.

Рисунок 9.9 — Рабочий чертеж детали поверхности вращения

Рисунок 9.10 — Рабочий чертеж детали «Вал»

9.1. Понятие о видах изделий и конструкторских документах

Изделием называют любой предмет или набор предметов производства, подлежащих изготовлению на предприятии.

ГОСТ 2.101-88* устанавливает следующие виды изделия:

• Детали;
• Сборочные единицы;
• Комплексы;
• Комплекты.

При изучении курса «Инженерной графики» к рассмотрению предлагаются два вида изделий: детали и сборочные единицы.

Деталь – изделие, изготавливаемое из однородного по наименованию и марке материала, без применения сборочных операций.

Например: втулка, литой корпус, резиновая манжета (неармированная), отрезок кабеля или провода заданной длинны. К деталям относятся так же изделия, подвергнутые покрытиям (защитным или декоративным), или изготовленные с применением местной сварки, пайки, склейки сшивки. К примеру: корпус, покрытый эмалью; стальной винт, подвергнутый хромированию; коробка, склеенная из одного листа картона, и т.п.

Сборочная единица – изделие, состоящее из двух и более составных частей, соединённых между собой на предприятии-изготовителе сборочными операциями (свинчиванием, сваркой, пайкой, клёпкой, развальцовкой, склеиванием и т.д.).Например: станок, редуктор, сварной корпус и т.д.

Комплексы — два и более специфицируемых изделия не соединенных на предприятии-изготовителе сборочными операциями, но предназначенных для выполнения взаимосвязанных эксплуатационных функций, например, автоматическая телефонная станция, зенитный комплекс и т.п.

Комплекты — два и более специфицированных изделия, не соединенных на предприятии-изготовителе сборочными операциями и представляющих набор изделий, имеющих общее эксплуатационное назначение вспомогательного характера, например, комплект запасных частей, комплект инструментов и принадлежностей, комплект измерительной аппаратуры и т.п.

Производство любого изделия начинается с разработки конструкторской документации. На основании технического задания проектная организация разрабатывает эскизный проект, содержащий необходимые чертежи будущего изделия, расчётно-пояснительную записку, проводит анализ новизны изделия с учётом технических возможностей предприятия и экономической целесообразности его осуществления.

Эскизный проект служит основанием для разработки рабочей конструкторской документации. Полный комплект конструкторской документации определяет состав изделия, его устройство, взаимодействие составных частей, конструкцию и материал всех входящих в него деталей и другие данные, необходимые для сборки, изготовления и контроля изделия в целом.

Сборочный чертёж – документ, содержащий изображение сборочной единицы и данные, необходимые для её сборки и контроля.

Чертёж общего вида – документ, определяющий конструкцию изделия, взаимодействие его составных частей и принцип работы изделия.

Спецификация – документ, определяющий состав сборочной единицы.

Чертёж общего вида имеет номер сборочной единицы и код СБ.

Например: код сборочной единицы (Рисунок 9.1) ТМ.0004ХХ.100 СБ тот же номер, но без кода, имеет спецификация (Рисунок 9.2) этой сборочной единицы. Каждое изделие, входящее в сборочную единицу, имеет свой номер позиции, указанный на чертеже общего вида. По номеру позиции на чертеже можно найти в спецификации наименование, обозначение данной детали, а также количество. Кроме того, в примечании может быть указан материал, из которого деталь изготовлена.

Диаметры окружностей

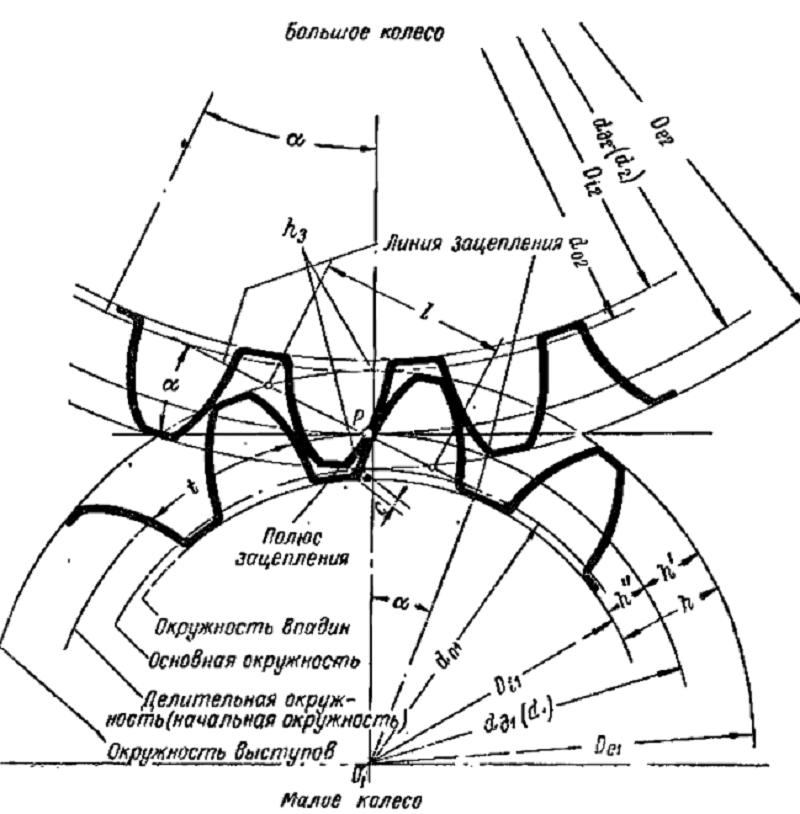
Рассмотрение геометрии зубчатых пар невозможно без определения диаметров. На каждой детали их выделяется несколько. Широкое распространение имеет диаметр окружности по выступам, иногда называемый диаметром вершин. Он определяет максимальные габариты диска колеса. Его противоположностью считается диаметр окружности впадин. Разность этих величин, поделенная пополам, дает полную длину зуба. Но этот параметр в чистом виде не используется. При расчетах принято выделять высоту головки и ножки зуба. Граница, отделяющая два этих понятия, называется делительной окружностью зубчатого колеса. Диаметр данной окружности выполняет функцию опорного параметра при выполнении расчетов геометрии, так как именно по ней определяется окружной шаг и модуль зацепления. Еще один диаметральный параметр, называемый основной окружностью, описывает теоретическую кривую, которая является базой при построении эвольвенты. Диаметр основной окружности используется для построения конкретного профиля зуба.

Характеристики и применение

Зубья шестеренки находятся в радиальных плоскостях. Линия контакта прямозубых цилиндрических шестерней параллельна оси вращения.

В зависимости от необходимых нагрузочных характеристик и точности передаваемого вращения, подбирается модуль (расстояние между центрами зубов) от 1 до 6.

Используется в подвижных частях механизмов соместно с зубчатой рейкой.

Цилиндрическая зубчатая передача применяется во всех типах автоматических ворот, конвейерных линиях с повышенной нагрузкой, 3D принтерах, станках ЧПУ и многом другом.

Параметры модуля шестерни

Рассматриваемая характеристика обозначается литерой m, указывает на прочность зубчатых передач. Единица измеряется в миллиметрах (чем выше нагрузка на передачу, тем больше модульное значение). В расчете параметра используются следующие показатели:

• диаметр делительной окружности;
• шаг и число зубьев;
• эвольвент (диаметр основной окружности);
• аналогичная характеристика впадин темной шестеренки;
• высота зуба темного и светлого колеса.

В машиностроительной отрасли расчеты ведутся по стандартным значениям для удобства изготовления и замены шестерен с числами от 1-го до 50-ти.

Что такое модуль на чертеже?

Модуль — это унифицированный элемент любых систем, состоящий из взаимозаменяемого комплекса деталей массового производства. Чертеж модуля выполняется на основании ГОСТ 2.109-73 — единая система конструкторской документации (ЕСКД).

Что представляет собой шестерня

Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.

Шестеренчатые передачи также имеют свою классификацию:

1. Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
2. Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
3. Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
4. Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.

Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.

При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.

Почему шестеренку называют так?

Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».

Расчет зубчатого колеса

Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.

Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.

1. Определение передаточного числа u.

2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.

3. Расчет зубьев передачи на изгиб.

4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).

5. Определение межосевого расстояния a_W из условия контактной прочности и округление его значения до стандартного.

6. Задание модуля из соотношения m = (0,01 – 0,02) х a_W и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.

7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.

8. Выбор коэффициентов формы зубьев для шестерни и колеса.

9. Проверка прочности зубьев по напряжениям изгиба.

10. Проведение геометрического расчета передачи.

11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.

Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.

Создаем 3D модель шестерни в программе Fusion 360.

Сейчас можно создать 3D модель для печати, на основании полученного эскиза. Для этого в программе Fusion 360 нажимаем на Sketch.

Выбираем плоскость, на которой будем создавать эскиз.

Затем в меню выбираем «Insert -> Insert SVG».

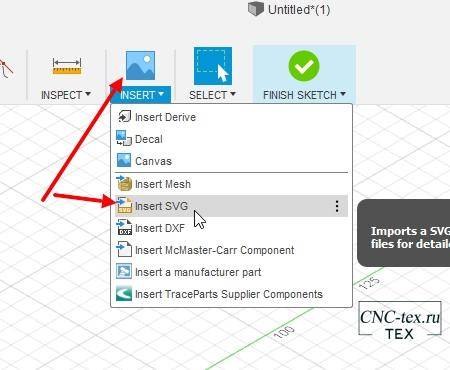
Нажимаем на кнопку загрузить с компьютера.

Выбираем файл, созданный в программе Inkscape.

Внимание, важный момент!!!! При загрузке создастся эскиз, но гораздо меньше. Необходимо рассчитать коэффициент увеличения

Иначе вы получите вот такой результат, оранжевые детали сделаны без коэффициента увеличения.

Для расчета коэффициента, рисуем квадрат 100 на 100 мм. Загружаем в программу Fusion 360. Замеряем размер и 100 делим на полученное значение. У меня получился вот такой коэффициент: «3,795498538733063». Полностью значение можно не вводить. Но чем точнее значение, тем меньше будет отклонение в размере изделия. Я указал 3,795498.

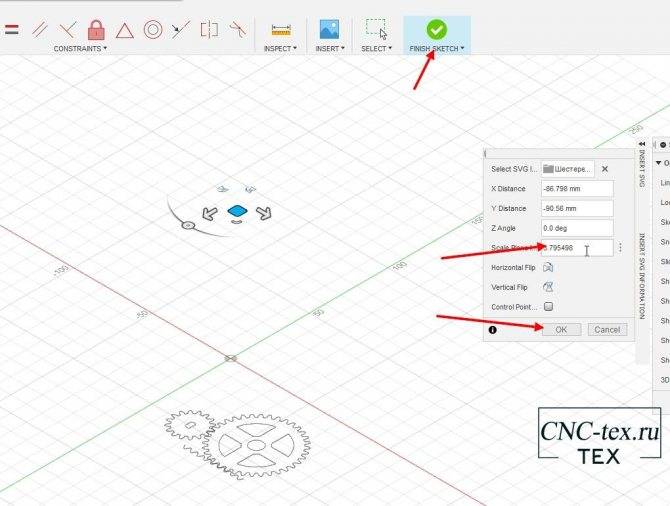
Затем выделяем деталь и нажимаем кнопку экстрадировать. Выдавливаем деталь на 5 мм.

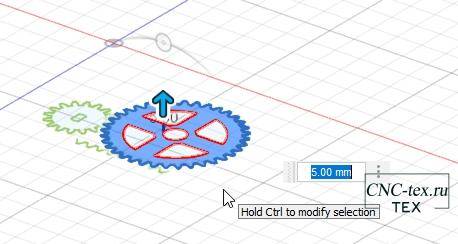
Вторую шестерёнку выдавливаем по аналогии.

Реечная передача в программе Fusion 360.

Если вы помните, мы не дорисовали реечную передачу в программе Inkscape. Поэтому нам нужно нарисовать её, для этого выбираем прямоугольник.

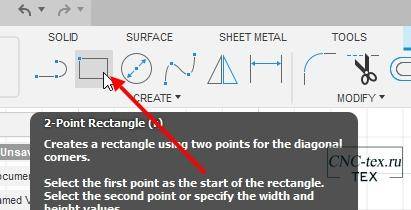
И рисуем по длине нашей рейки, нужной высоты.

Удаляем сторону прямоугольника, где у нас нарисованы зубцы рейки.

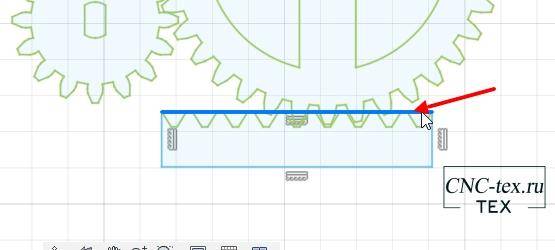
Затем экстрадируем полученную деталь.

В итоге получаем вот такой результат.

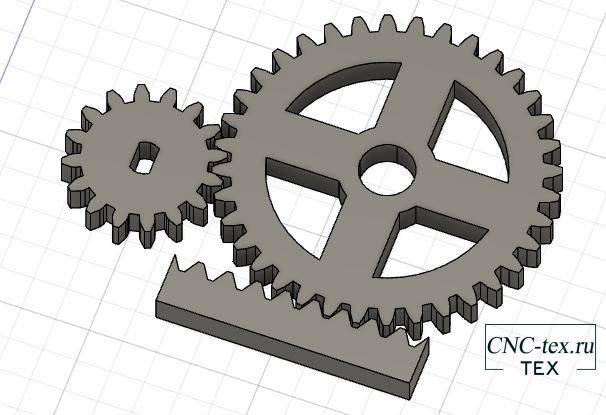
Как видим, все детали соединены точно так же, как и мы их нарисовали в программе Inkscape.