Конусность и уклон: построение, расчет, обозначение

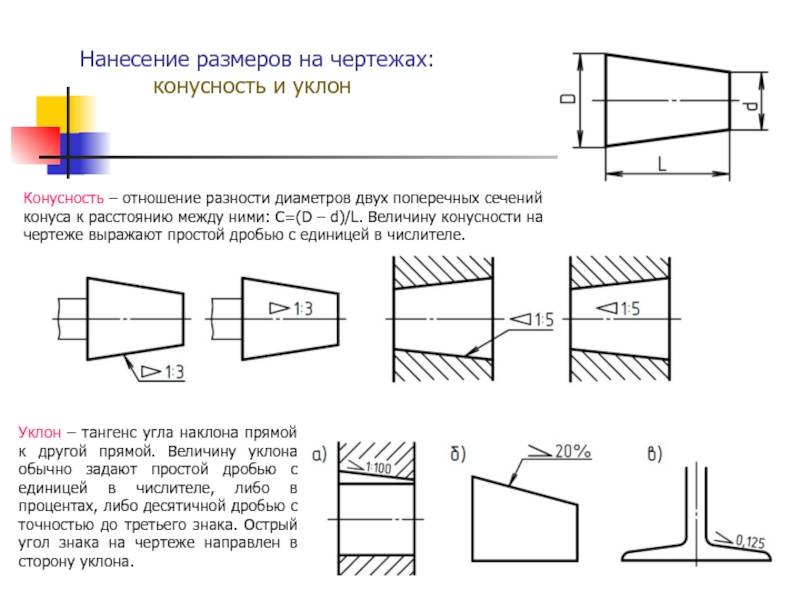
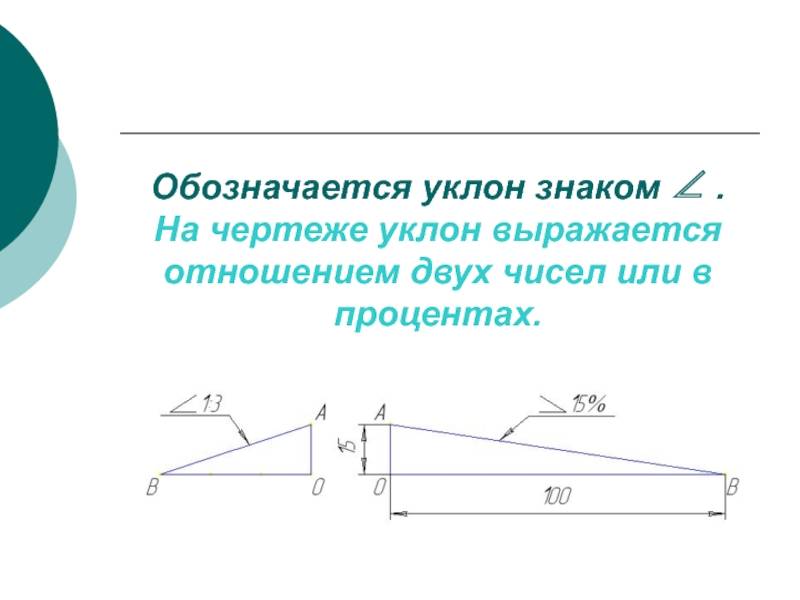
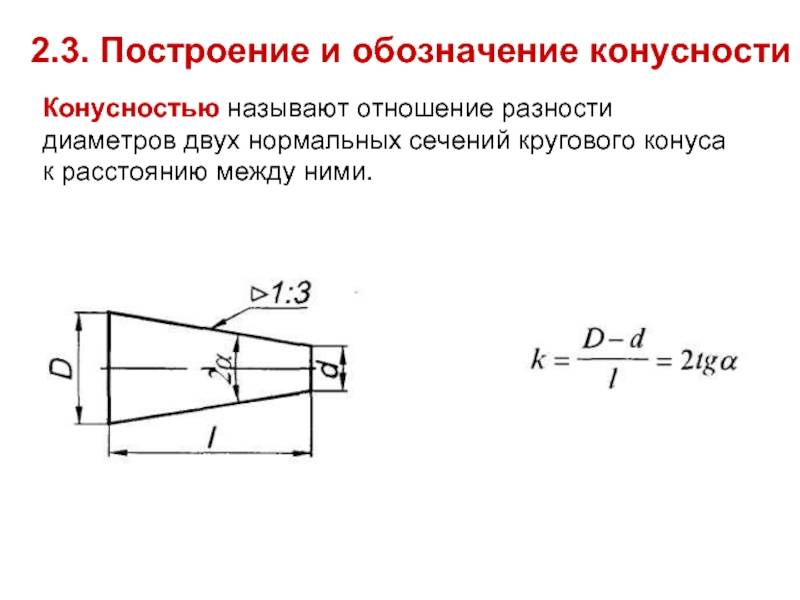
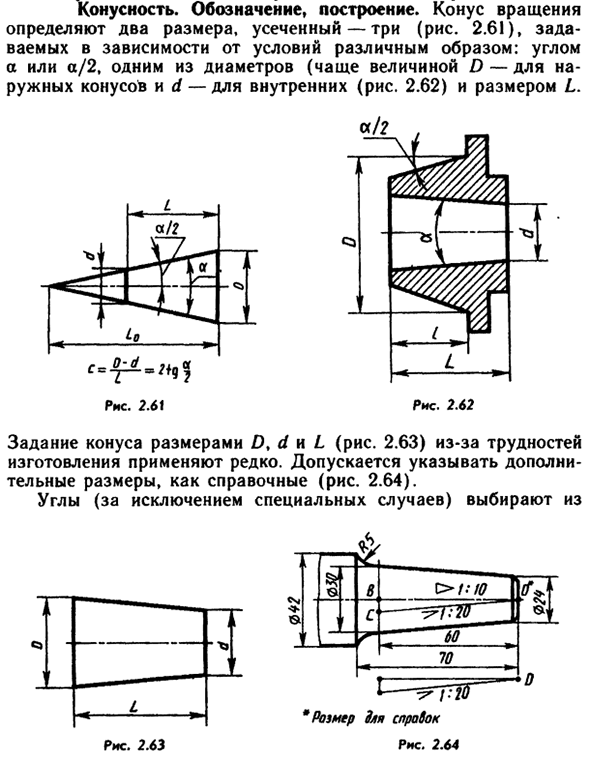
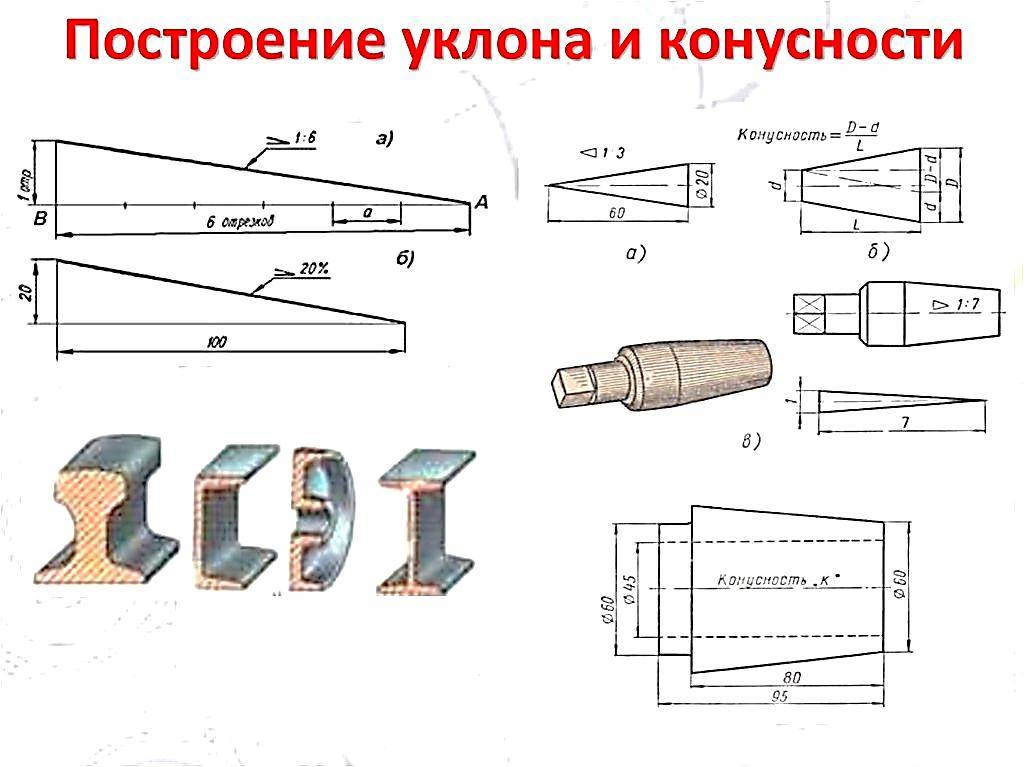
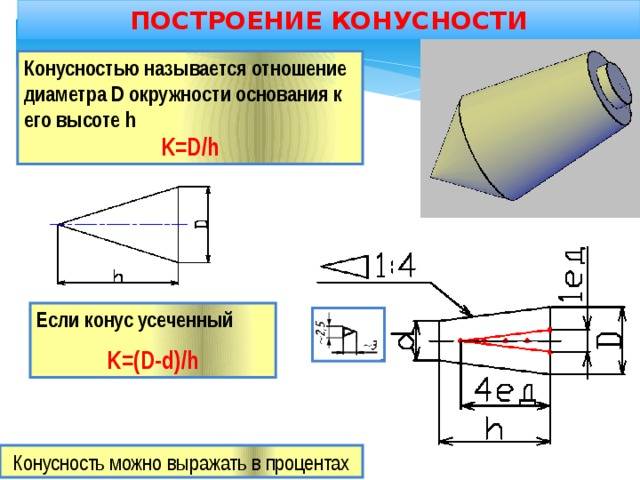
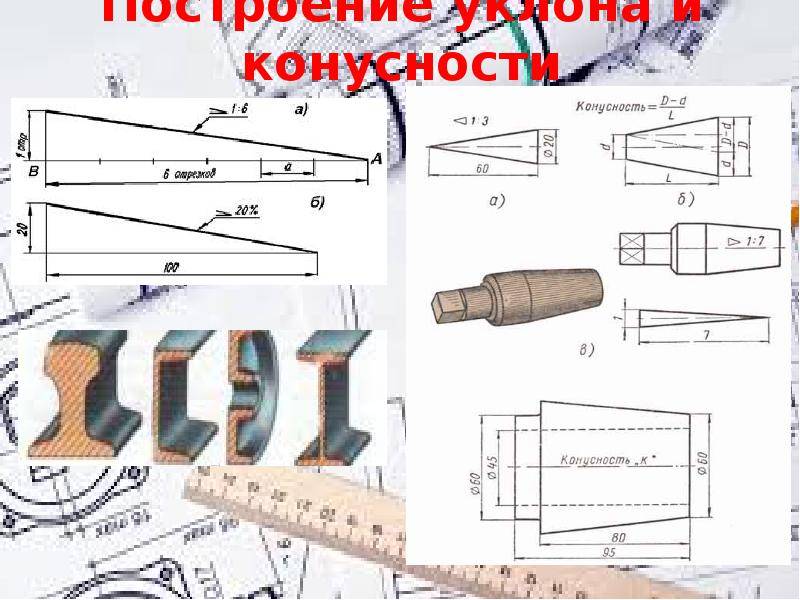
Построение уклона и конусности

Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:

1. Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
2. В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
3. С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.

На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:

1. Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
2. Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
3. Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
4. Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
5. Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.

Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:

1. Программа при построении наклонных линий автоматически отображает угол. Проведенные расчеты в этом случае позволяют проводить построение даже в том случае, если нет информации об большом или малом, промежуточном диаметре. Конечно, требуется информация, касающаяся расположения диаметров относительно друг друга.
2. Есть возможность использовать дополнительные инструменты, к примеру, привязку для построения нормальной конусности. За счет этого существенно прощается поставленная задача и ускоряется сама процедура. При черчении от руки приходится использовать специальные инструменты для контроля подобных параметров.
3. Длина всех линий вводится числовым методом, за счет чего достигается высокая точность. Погрешность может быть допущена исключительно при применении низкокачественного устройства для вывода графической информации.
4. Есть возможность провести замер всех показателей при применении соответствующих инструментов.
5. Для отображения стандартов используются соответствующие инструменты, которые также существенно упрощают поставленную задачу. Если программа имеет соответствующие настройки, то достаточно выбрать требуемый инструмент и указывать то, какие размеры должны быть отображены. При этом нет необходимости знания стандартов, связанных с отображением стрелок и других линий.

Уклоны и конусность — Техническое черчение

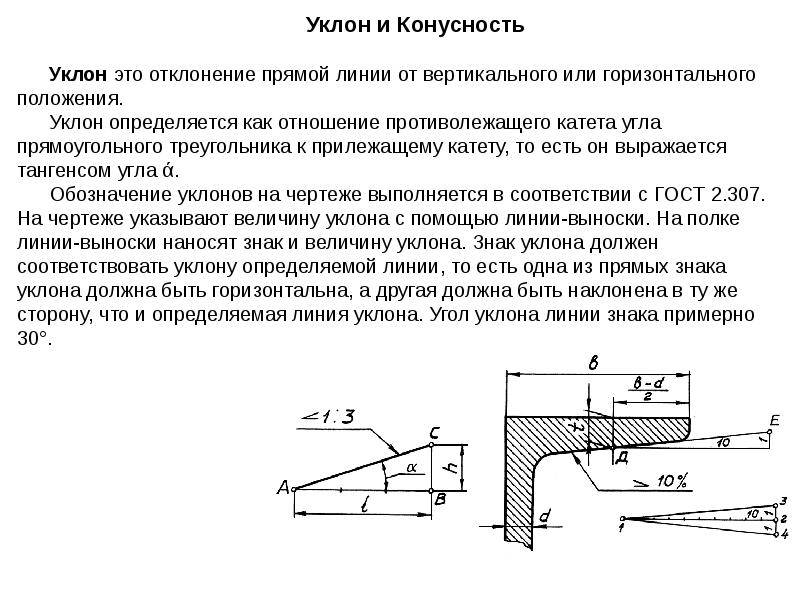
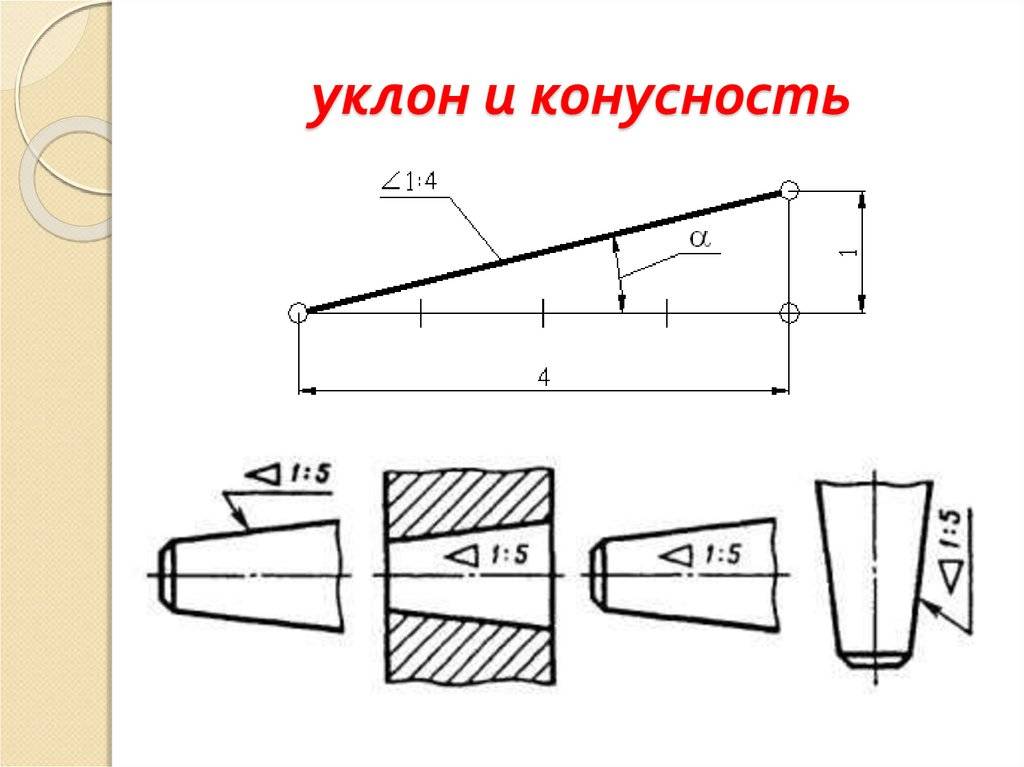
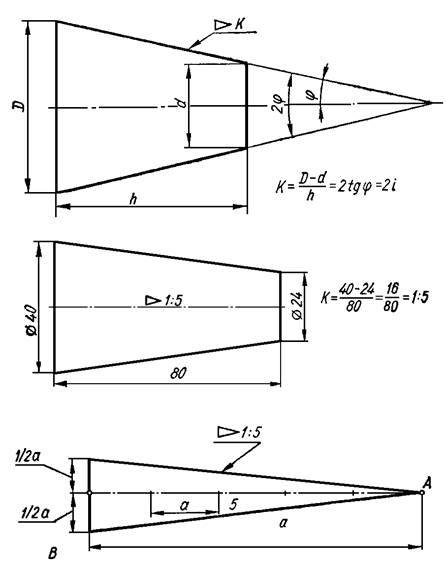
• Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:
• i=AC/AB=tga
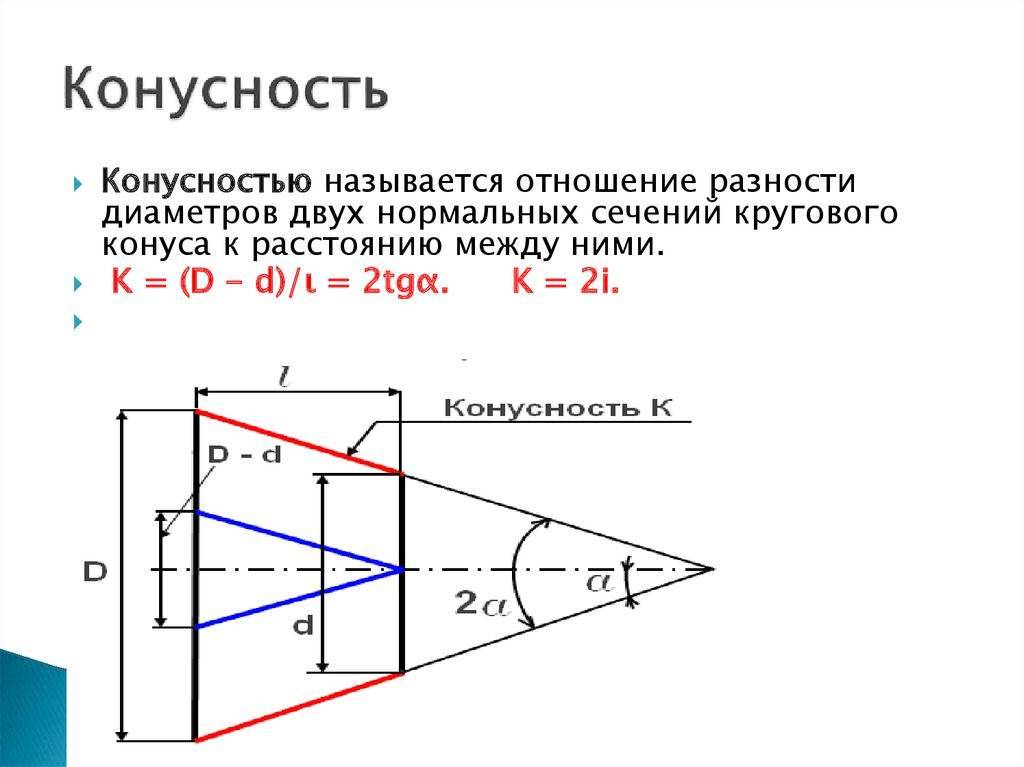
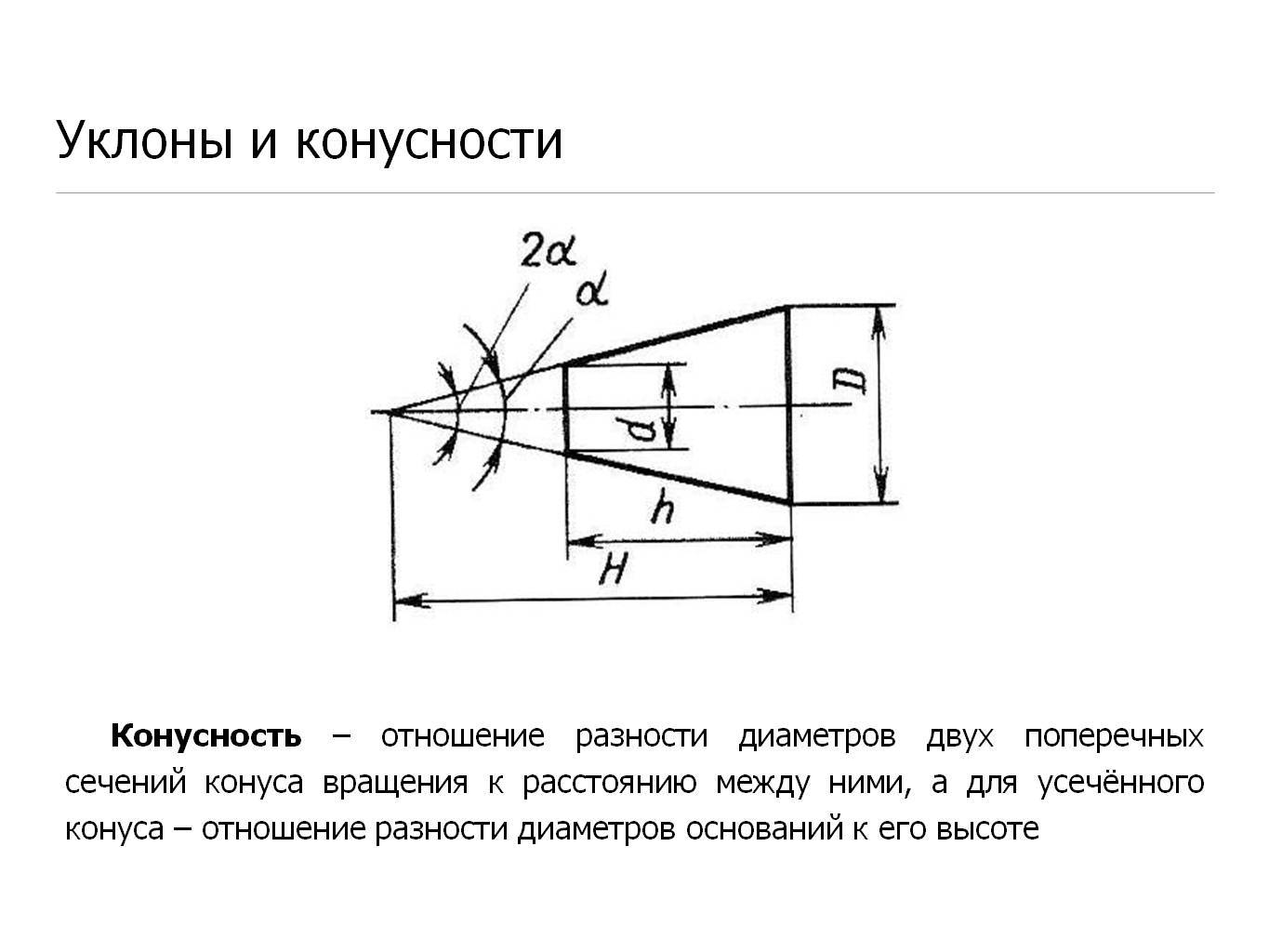
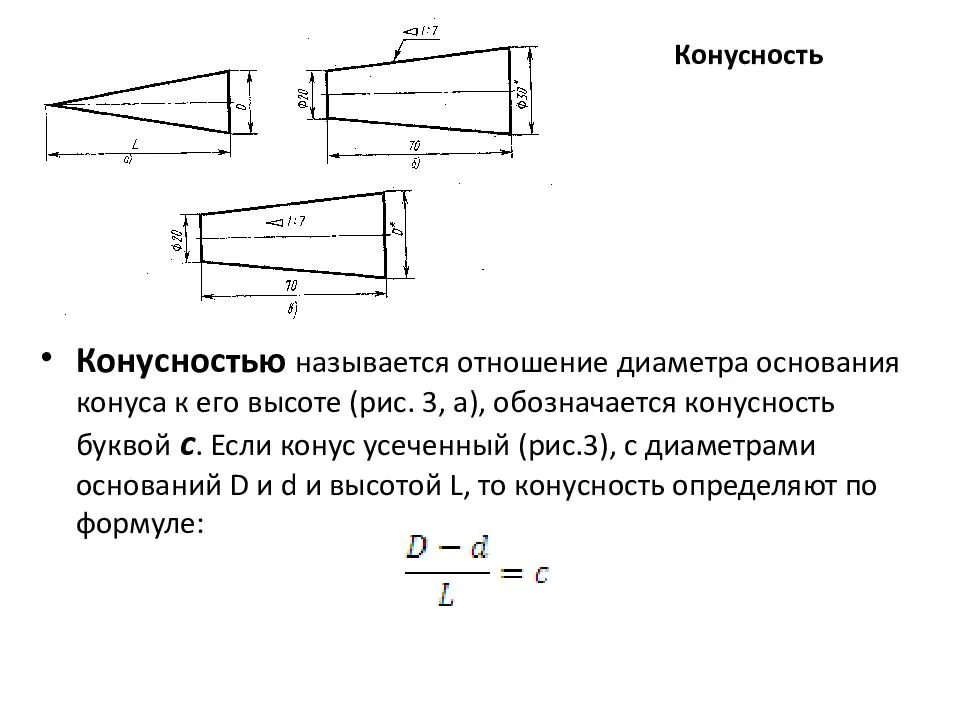
• Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)
• k=(D-d)/l=2tga
• Таким образом,
• k = 2i
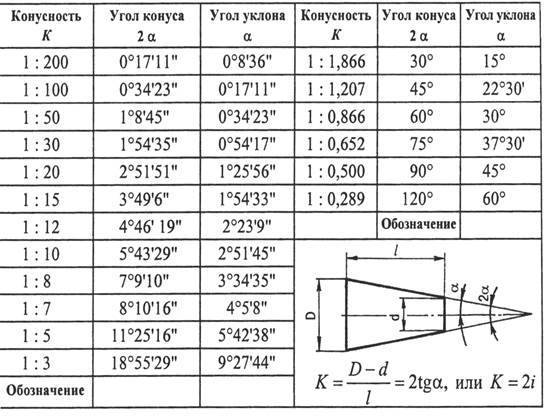
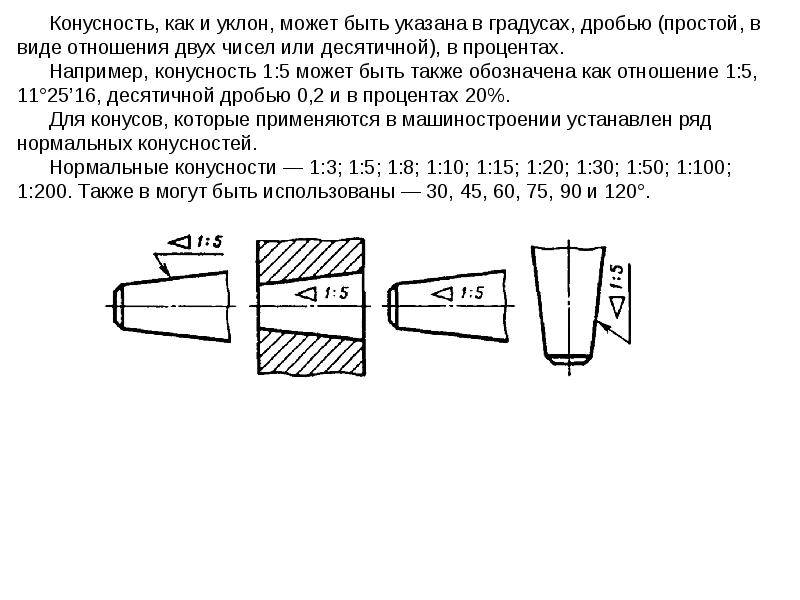
• Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.
• Например: конусность, выраженная в градусах — 11°25’16″; отношением —  1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38″; отношением — 1:10; дробью—0,1; в процентах —  10%.
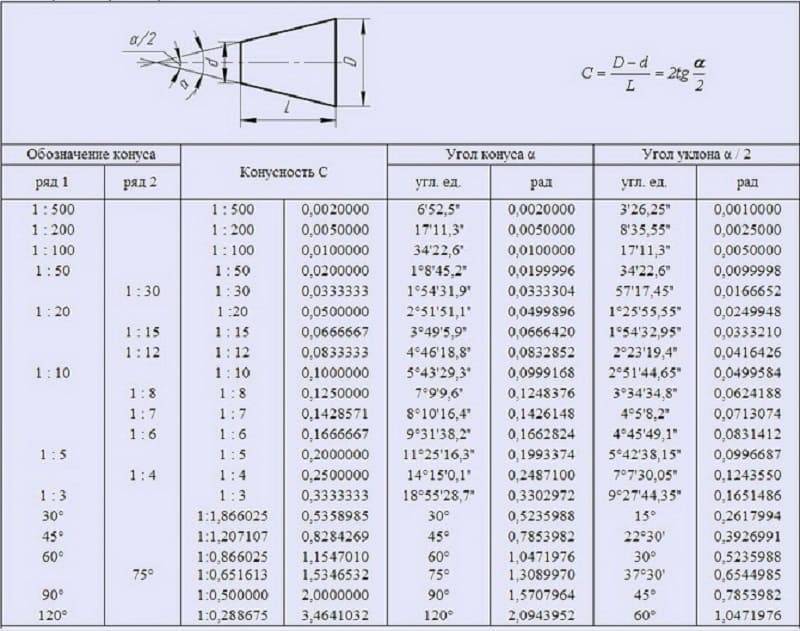
• Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.
• Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

1. Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):
2. 1)    построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2)    опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

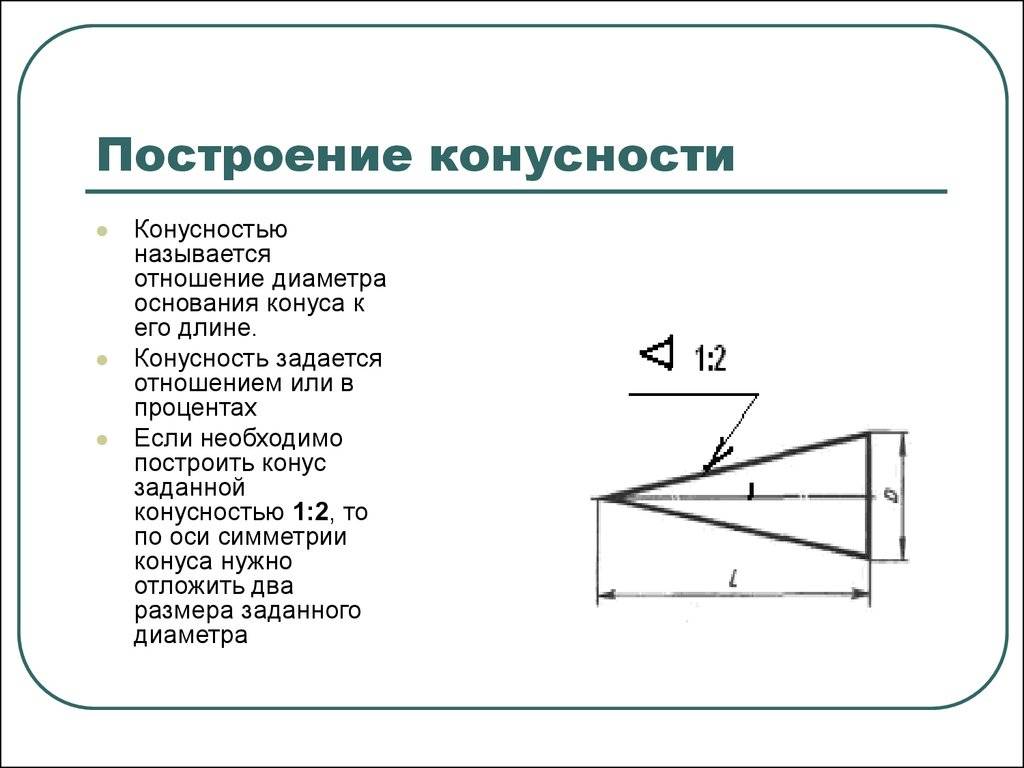
Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

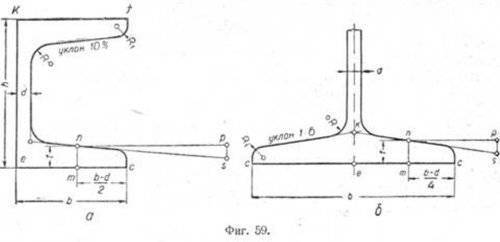
Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм.

Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2.

В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

• Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:
• ps/np=10/100,
• откуда
• ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

1. i=ps/np=1/6
2. где i — заданный уклон.
3. Подставив в формулу числовые значения, получим
4. ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.

История определения конуса

Геометрия как наука появилась из практических требований строительства и наблюдений за природой. Постепенно опытные знания обобщались, а свойства одних тел доказывались через другие. Древние греки ввели понятие аксиом и доказательств. Аксиомой называется утверждение, полученное практическим путем и не требующее доказательств.

В своей книге Евклид привел определение конуса как фигуры, которая получается вращением прямоугольного треугольника вокруг одного из катетов. Также ему принадлежит основная теорема, определяющая объем конуса. А доказал эту теорему древнегреческий математик Евдокс Книдский.

Другой математик древней Греции, Аполлоний Пергский, который был учеником Евклида, развил и изложил теорию конических поверхностей в своих книгах. Ему принадлежит определение конической поверхности и секущей к ней. Школьники наших дней изучают Евклидову геометрию, сохранившую основные теоремы и определения с древних времен.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

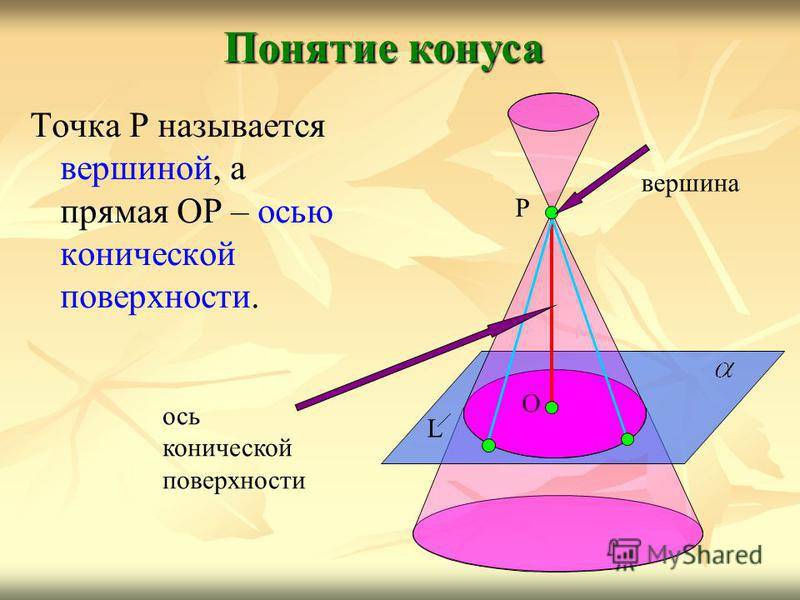
Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

4

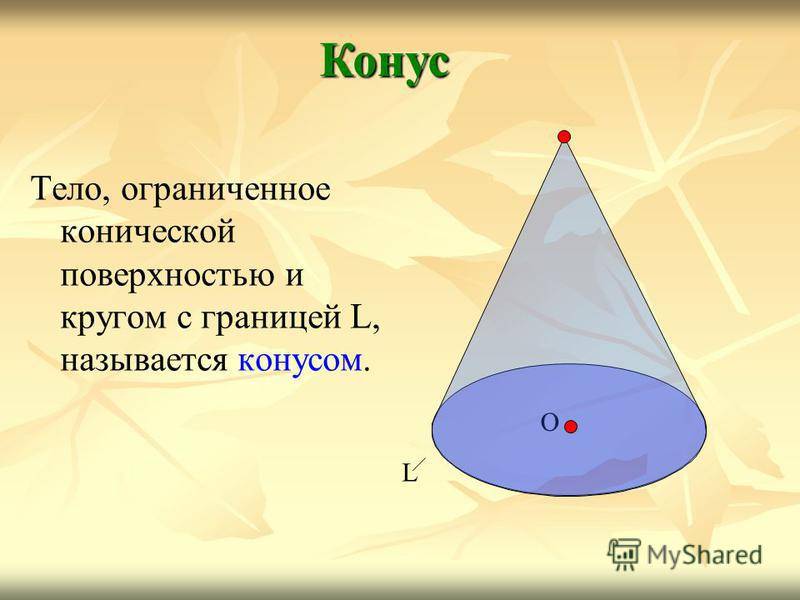
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

5

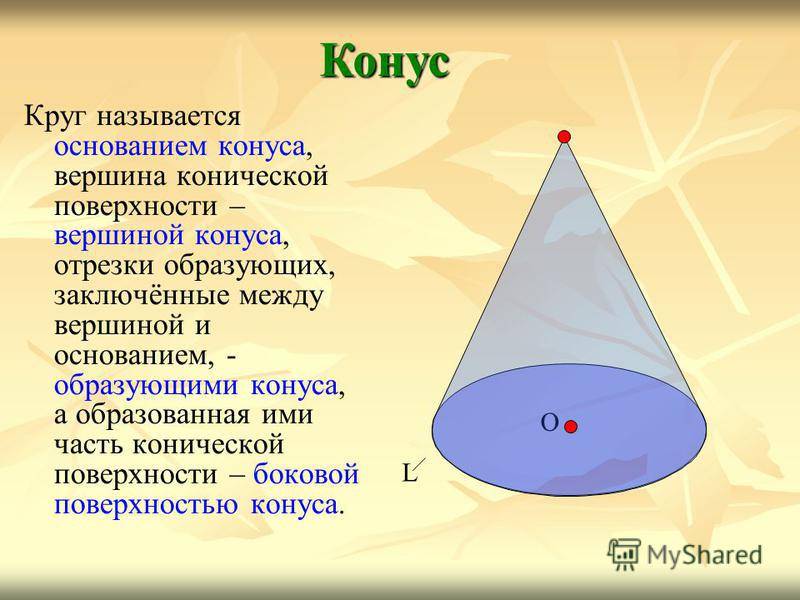
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

6

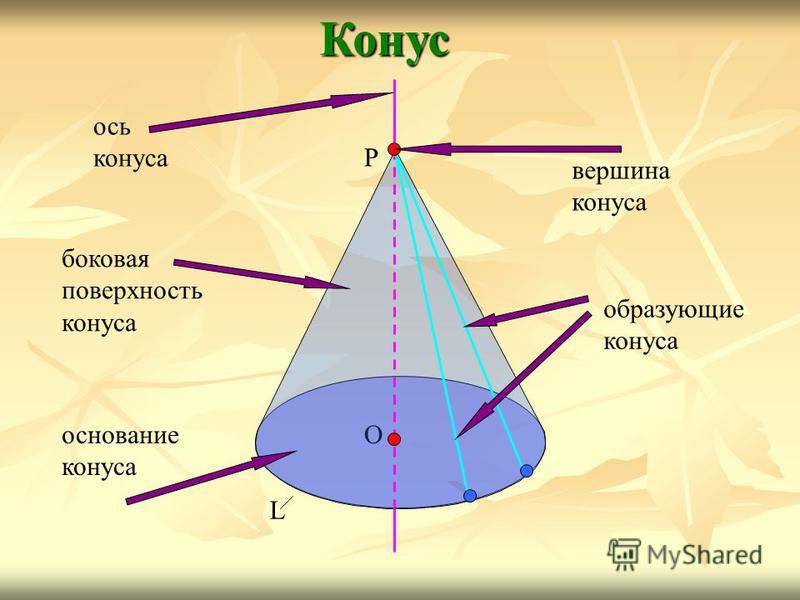
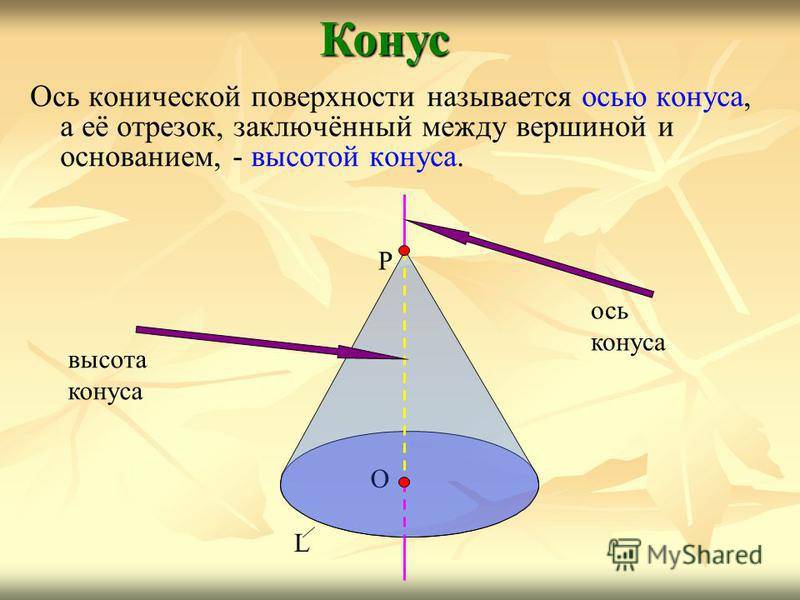
Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

7

Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

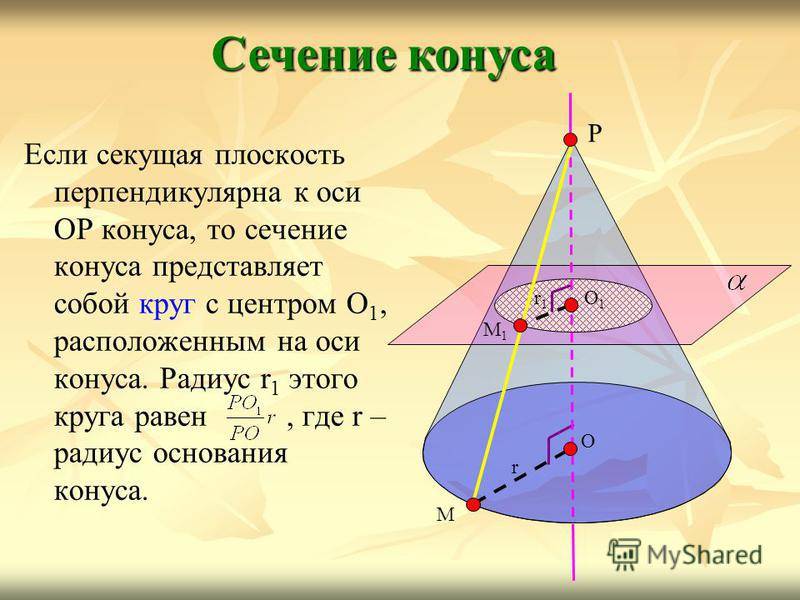
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

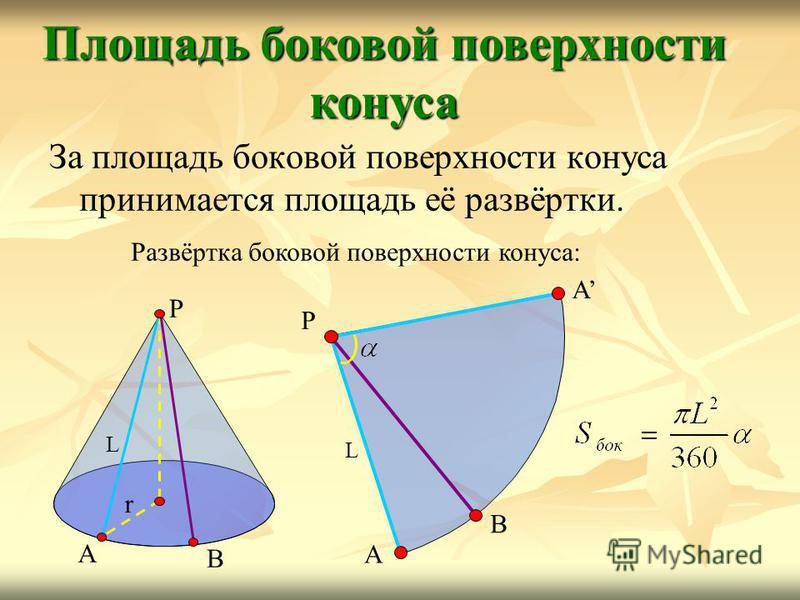
За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

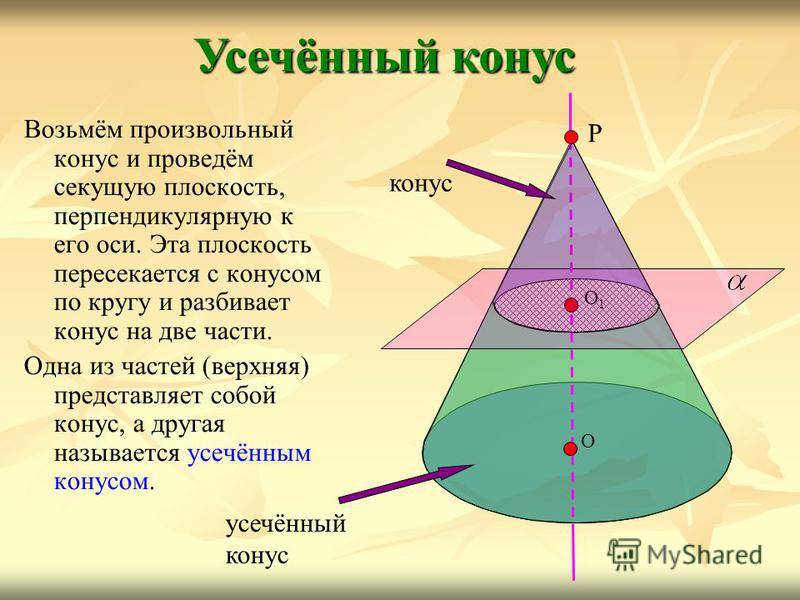
Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

16

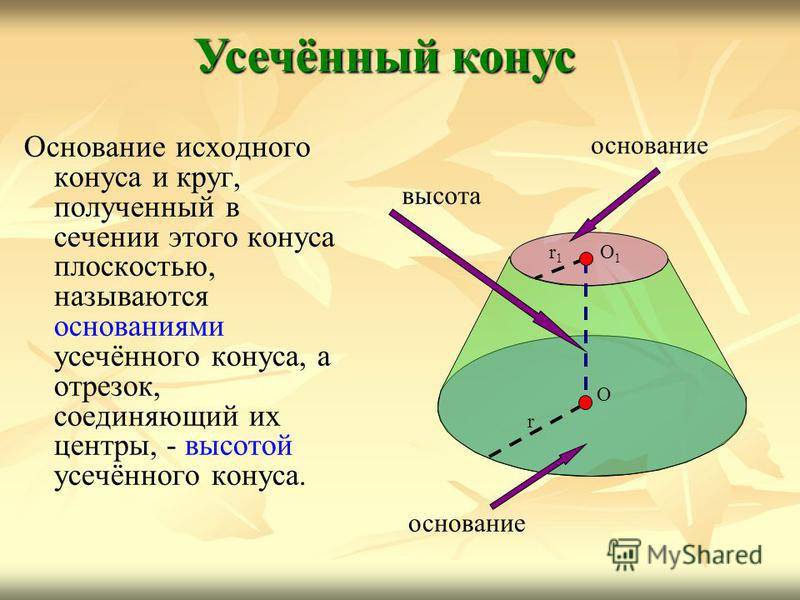
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

17

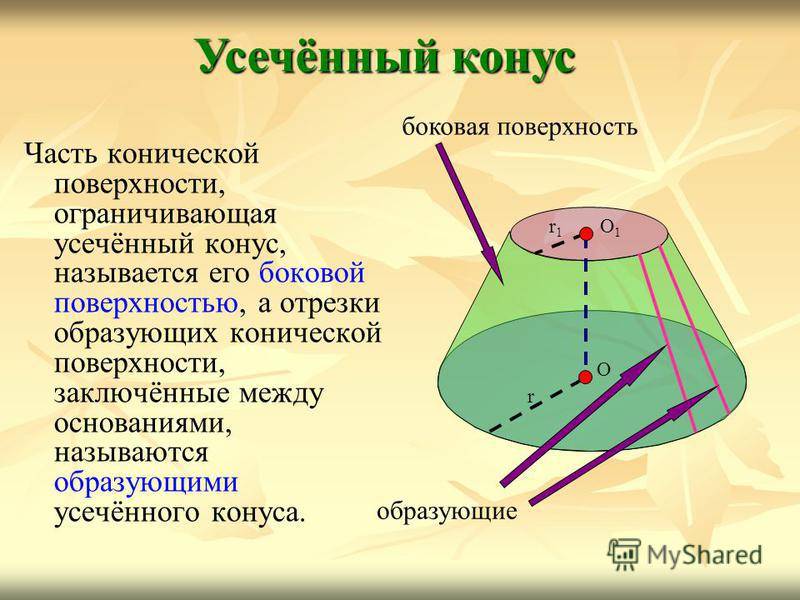
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

18

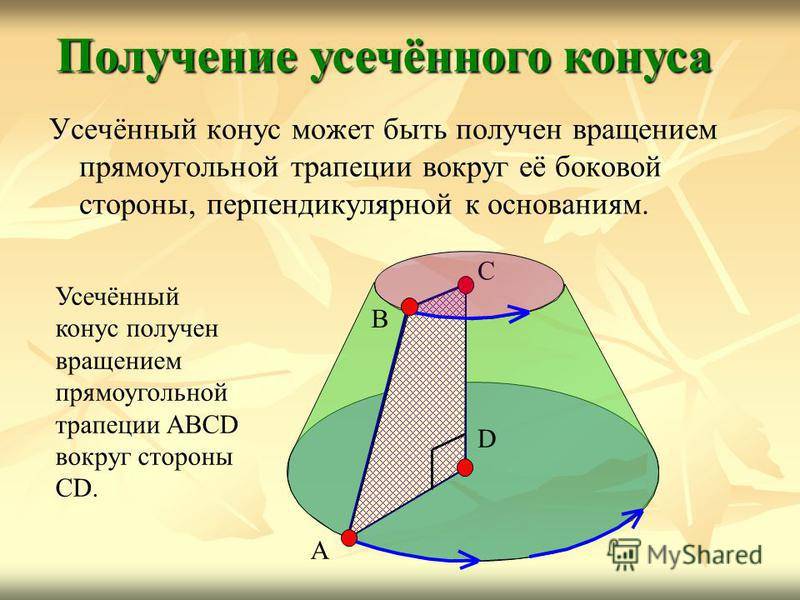
Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

19

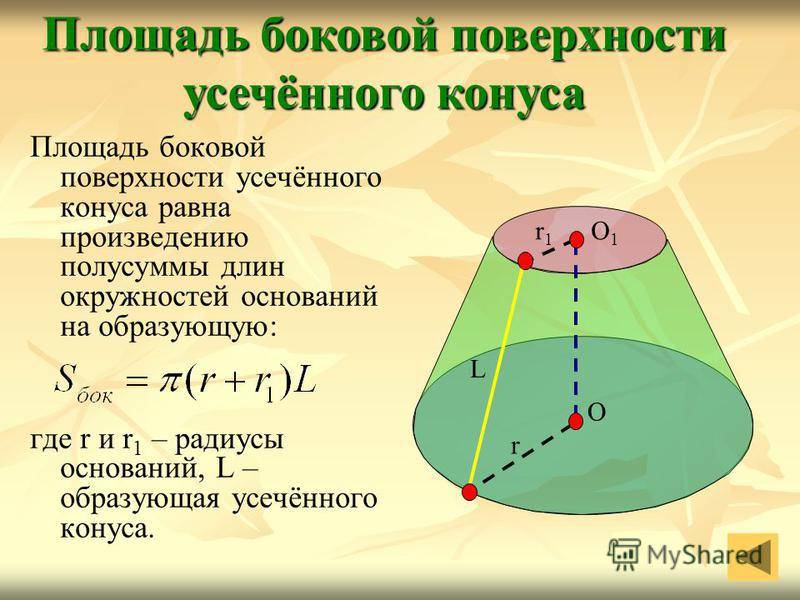
Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

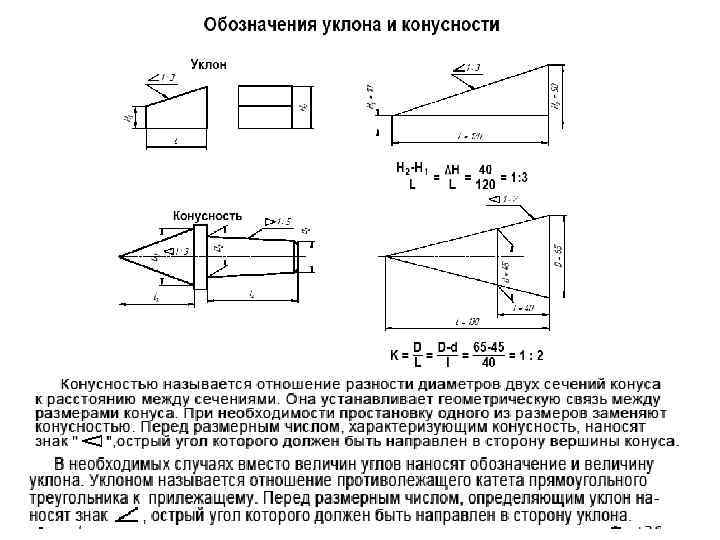
Обозначение уклона в строительстве

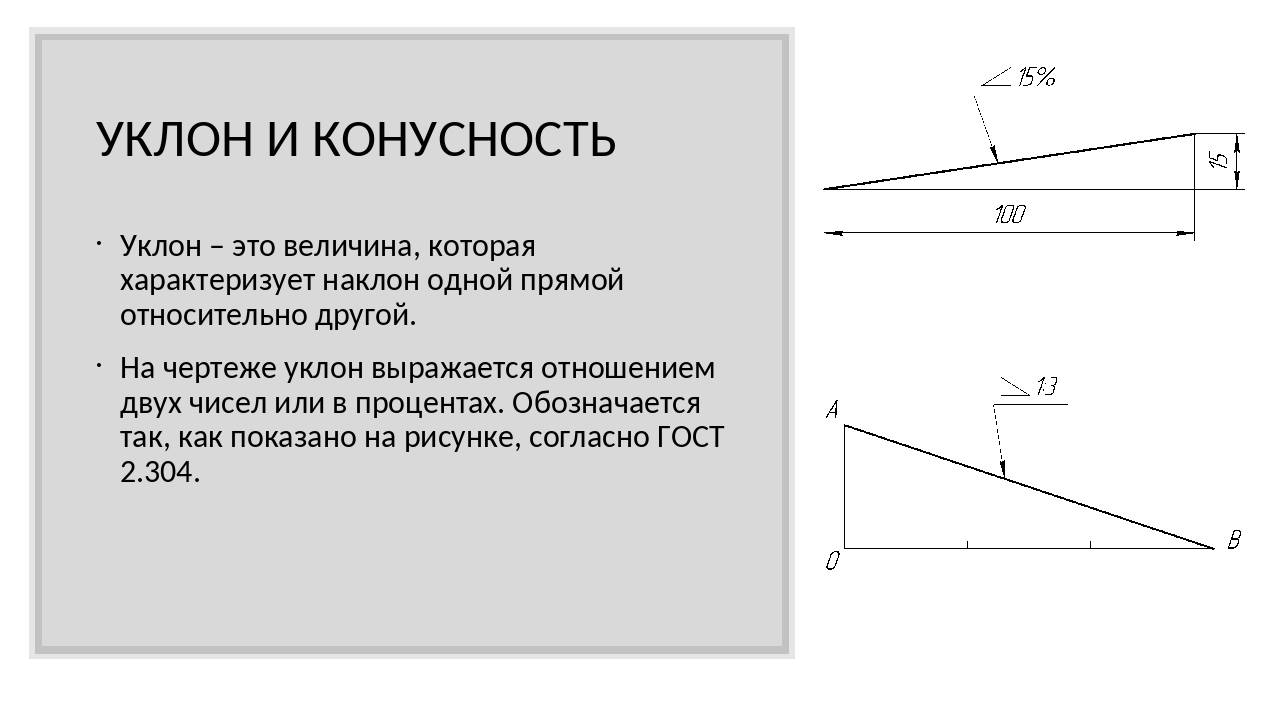
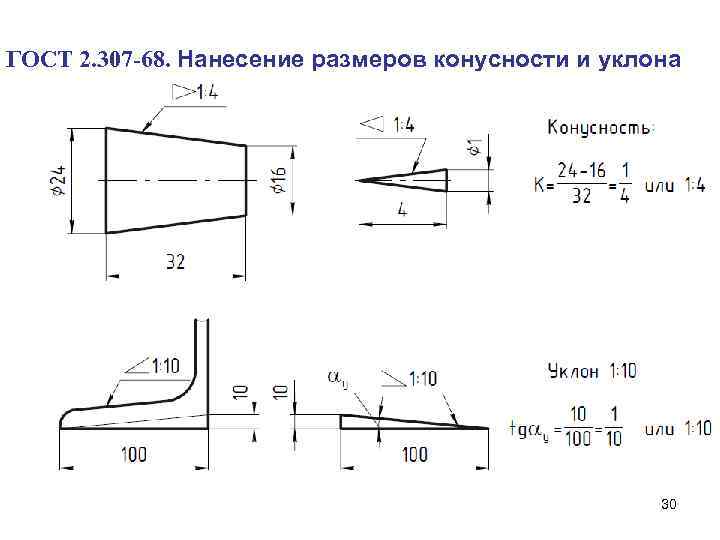
Угол уклона — показатель наклона какой либо поверхности (дороги, крыши, пандуса, лестничного марша и пр.) относительно уровня горизонта.Угловые размеры указывают на чертежах в градусах, минутах и секундах с обозначением единицы измерения (ГОСТ 2.307-2011 «Единая система конструкторской документации (ЕСКД). Нанесение размеров и предельных отклонений«).

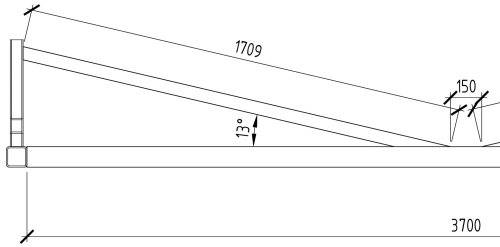
В соответствии с ГОСТ Р 21.1101-2013 «Система проектной документации для строительства (СПДС). Основные требования к проектной и рабочей документации», на планах направление уклона плоскостей указывают стрелкой, над которой при необходимости проставляют числовое значение уклона в процентах или в виде отношения единицы высоты плоскости к соответствующей горизонтальной проекции. Допускается числовое значение уклона указывать в промилле или в виде десятичной дроби с точностью до третьего знака.

На разрезах, сечениях и схемах перед размерным числом, определяющим числовое значение уклона, наносят знак,

острый угол которого должен быть направлен в сторону уклона (кроме крутизны откосов насыпей и выемок). Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.

Также вместо знака угла, на чертежах встречается и буквенное обозначение уклона ( i ).

В процентах обычно обозначают углы уклонов крыш, пандусов, лестничных маршей и т.п.

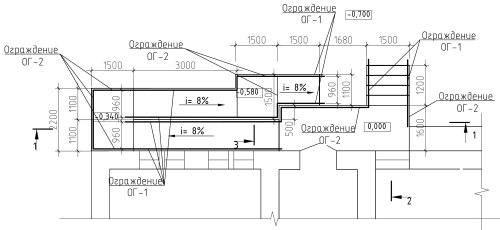
В промилле обозначают углы уклонов плоскостных сооружений — спортивные игровые площадки, поля, беговые дорожки, а также линейные сооружения — автомобильные и железные дороги.

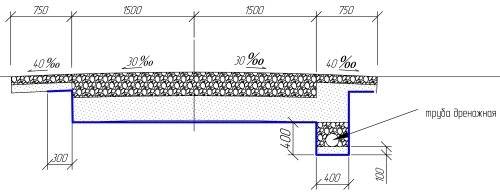
Процент ( % ) — одна сотая доля. Промилле ( ‰ ) — одна тысячная доля.

Например: уклон при высоте 0,2 метра и протяженностью по горизонтали 4 метра будет равен 5 % (читается как — пять сотых) или 50 ‰ (читается как — пятьдесят тысячных), это значение также будет соответствовать приблизительно — 3 о .

Часто спрашивают, что означает уклон, на пример 0,05 — это соотношение высоты к длине горизонтального участка (0,2 м / 4 м = 0,05 — см. чертеж 1), которое при необходимости можно перевести в проценты или промилле, смотря что требуется.

Для определение угла уклона в процентах (%) (см. чертеж 1) необходимо: 0,2 м / 4 м х 100 = 5 %.

Для определение угла уклона в промилле (‰) необходимо: 0,2 м / 4 м х 1000 = 50 ‰.

Ту же величину уклона можно обозначить и как соотношение высоты к длине горизонтального участка — 1:20 (4 / 0,2 = 20).

Если требуется определить протяженность горизонтального участка, зная величину уклона в процентах и его высоту из чертежей, необходимо — 0,2 м / (5 % / 100) = 4 м.

Чтобы определить высоту уклона, зная величину уклона в процентах и протяженность участка из чертежей, необходимо — 5 % / 100 х 4 м = 0,2 м.

Аналогичным образом вычисляются размеры для угла уклона выраженного в промилле, только вместо деления на 100, выполняется деление на 1000.

Примечание: для того чтобы ввести на компьютере символ промилле (‰), необходимо включить NumLock, нажать клавишу Alt и удерживая ее набрать на цифровом блоке клавиатуры 0137, отпустить клавишу Alt после чего появится символ ‰.

Если требуется определить уклон с точностью до 1 градуса, нужно: 0,2 м / 4 м = 0,05. Полученное число — 0,05 необходимо найти в таблице tg (тангенсов) для углов. Приближенное значение в таблице — 0,0524, будет соответствовать углу 3 о (см. таблицу).

Источник

Задача на определение площади и объема усеченного конуса

Ниже на рисунке изображен усеченный конус и приведены его линейные параметры. Необходимой найти площадь поверхности и объем фигуры.

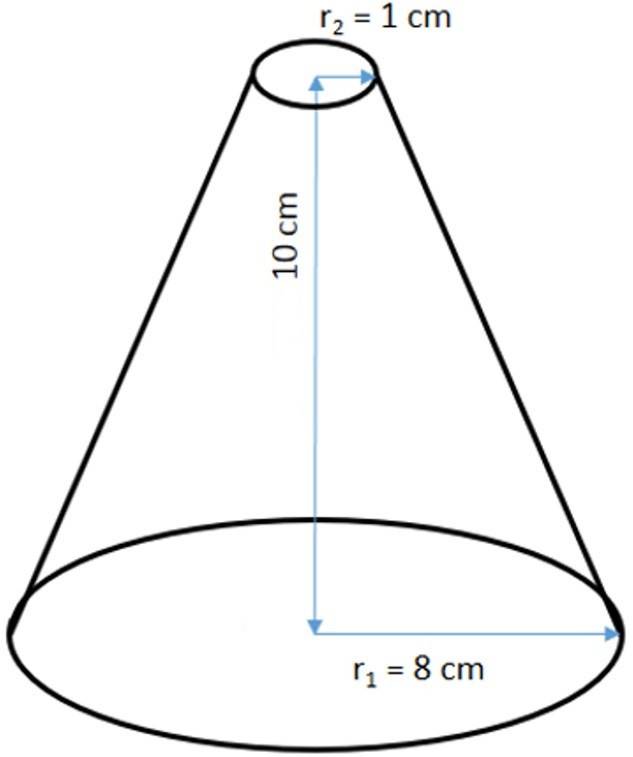
Начнем решать задачу с определения величины V. Ее вычисление не представляет никакого труда, поскольку известны все необходимые параметры. Подставляя их в формулу для V, получаем:

Найденное значение соответствует 0,76 литра.

Чтобы найти площадь поверхности S, следует сначала вычислить длину образующей g фигуры. Она будет равна:

Значение образующей g мы округлили до сотых. Теперь можно воспользоваться формулой для площади S:

Заметим, что формулы для V и S, которые мы использовали при решении задачи, справедливы только для круглого прямого усеченного конуса. В случае наклонной фигуры или же фигуры с некруглыми основаниями этими формулами пользоваться нельзя.

Специальная резьба. Резьба усиленная упорная

Резьба упорная усиленная применяется для особо больших нагрузок (и для диаметров 80…2000 мм.) с углом профиля 45° по ГОСТ 13535-87. Условное обозначение, например: S 45 ° × 200 × 12, где 12 – шаг резьбы, который указывают обязательно.

Специальную резьбу со стандартным профилем, но нестандартным шагом или диаметром обозначают Сn и условное обозначение профиля, например: Сn М40´1,5-6g.

Профиль квадратной резьбы не стандартизирован, но эта резьба имеет применение в соединениях, где не должно быть самоотвинчивания под действием приложенной нагрузки. Поэтому на чертеже приводят все данные, необходимые для ее изготовления. На рис. 4.18 показана прямоугольная двухзаходная резьба на стержне.

Рис. 4.18. Прямоугольная резьба

Обозначения типов резьб приведены в табл. 4.1, примеры обозначения типов резьб показаны в табл. 2.

Обозначения типов резьбы

Тип резьбы	Стандарт	Условное обозначение	Указывается	Пример обозначения
Метрическая скрупным шагом	ГОСТ 9150-81 ГОСТ 24705-81 ГОСТ 8724-81 ГОСТ 16093-81	М	Номинальный диаметр резьбы, шаг, направление, поле допуска.	M20-6g M20LH-6g
Метрическая с мелким шагом	ГОСТ 9150-81 ГОСТ 24705-81 ГОСТ 8724-81 ГОСТ 16093-81	М	Номинальный диаметр резьбы, шаг, направление, поле допуска.	M20×1,5-6g M20×1,5LH-6H
Трубная цилиндрическая	ГОСТ 6357-81 ГОСТ 3262-75* ГОСТ 8957-75*	G	Условное обозначение резьбы в дюймах, класс точности среднего диаметра резьбы А или В, длина свинчивания, если она больше, установленной стандартом.	G 1 /4-A G1LH-B-40
Трубная коническая	ГОСТ 6211-81	R – наружная Rс – внутренняя	Условные обозначения резьбы в дюймах, направление (левое).	R1 1 /2LH Rc1 1 /2LH
Дюймовая	ОСТ НКТП 1260	Номинальный диаметр резьбы в дюймах	1 1 /2″ ОСТНКТП 1260
Коническая дюймовая	ГОСТ 6111-52*	К	Условное обозначение резьбы в дюймах.	K 3 /4″ ГОСТ 6111-52
Метрическая коническая	ГОСТ 25229-82	МК	Значение диаметра резьбы в основной плоскости с указанием при необходимости шага и направления	MK20×1,5LH MK20×1,5
Круглая	ГОСТ 6042-83 ГОСТ 13536-68 СТ СЭВ 3293-81*	Е	Диаметр резьбы	E14 ГОСТ 6042-83
Кр	Номинальный диаметр, шаг	Kp.12×2,54 ГОСТ 13536-68
Rd	Диаметр резьбы	RD16 Rd16LH
Трапецеидальная	ГОСТ 9484-81 ГОСТ 9562-81 ГОСТ 24739-81*	Тr	Номинальный диаметр резьбы, ход Ph, шаг P, поле допуска, при необходимости – длину свинчивания	Tr 80×40(P10)-6e Tr 40×6-8e Tr 80×40(P10)-8e-180

Окончание табл. 4.1

Тип резьбы	Стандарт	Условное обозначение	Указывается	Пример обозначения
Упорная	ГОСТ 10177-82 ГОСТ 25096-82	Номинальный диаметр резьбы, ход Ph, шаг P, поле допуска.	S80×20(P5)-7h S80×20LH-7H
Упорная усиленная	ГОСТ13535-87	S45°	Угол профиля 45°, номинальный диаметр, шаг	S45°×200×12
Специальная	–	Сn	Условное обозначение профиля, номинальный диаметр, шаг (при необходимости), поле допуска.	Cn M40×1,5-6g

Примеры обозначений наиболее употребительных видов резьбы

Деталь	Обозначение резьбы	Надо читать
Резьба метрическая, наружный диаметр резьбы 20 мм., с крупным шагом, правая, поле допуска 6g
М25х1.5LH-6g	Резьба метрическая, наружный диаметр резьбы 25 мм., шаг 1,5 мм, мелкий, левая, поле допуска 6g
1 1 /2²×ОСТ НКТН 1260	Резьба дюймовая, наружный диаметр 1½” (38,1 мм), правая, ОСТ НКТП 1260
Резьба трубная, обозначение размера , правая, класс точности средний диаметр резьбы А, длина свинчивания 20 мм.

Продолжение табл.4. 2

Деталь	Обозначение резьбы	Надо читать
Резьба коническая, дюймовая, наружный диаметр ¾” (в основной плоскости 26,4 мм), правая; ГОСТ 6111-52
Резьба трапецеидальная, однозаходная, нормальная, наружный диаметр 30 мм, шаг 6 мм, левая, поле допуска 8е
Резьба упорная, нормальная, наружный диаметр резьбы 50 мм, шаг 6 мм, двухзаходная, ход 12, правая, поле допуска 7h
Резьба специальная, со стандартным профилем метрической резьбы, наружный диаметр 58 мм, шаг 3 мм, поле допуска 6g.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения:Студент – человек, постоянно откладывающий неизбежность. 10933 – | 7420 – или читать все.

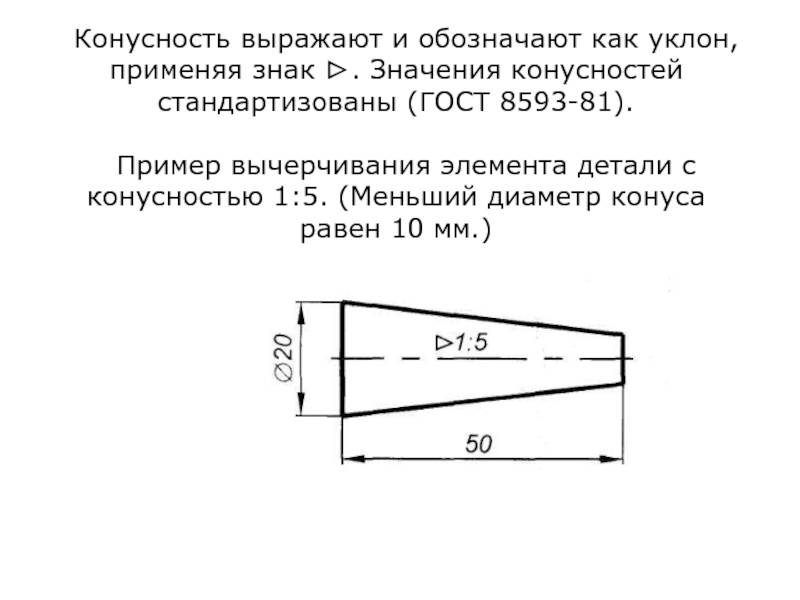
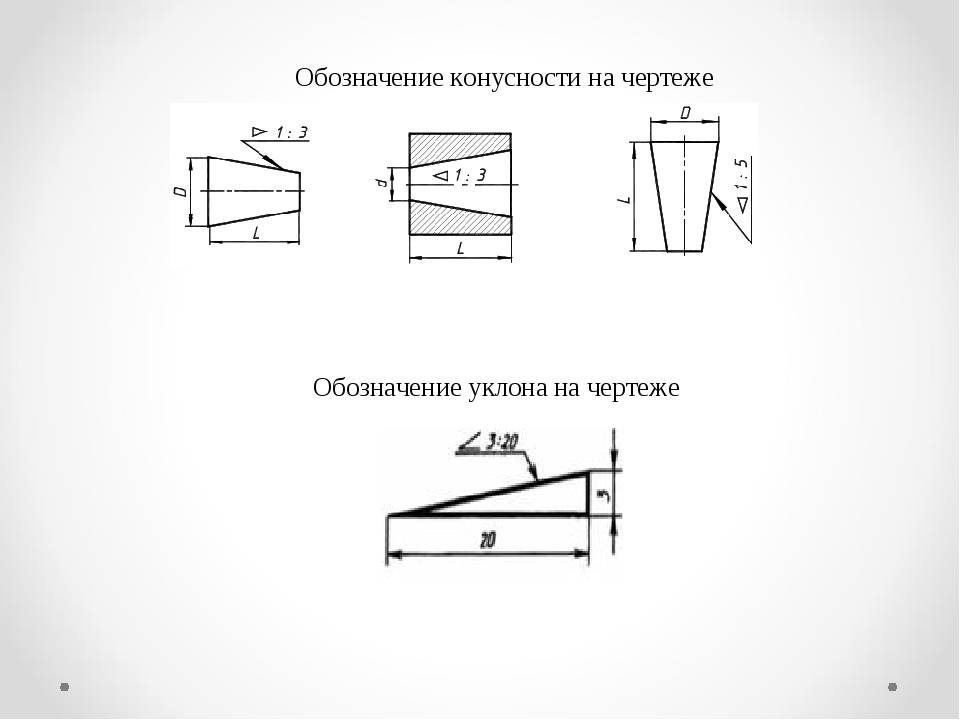
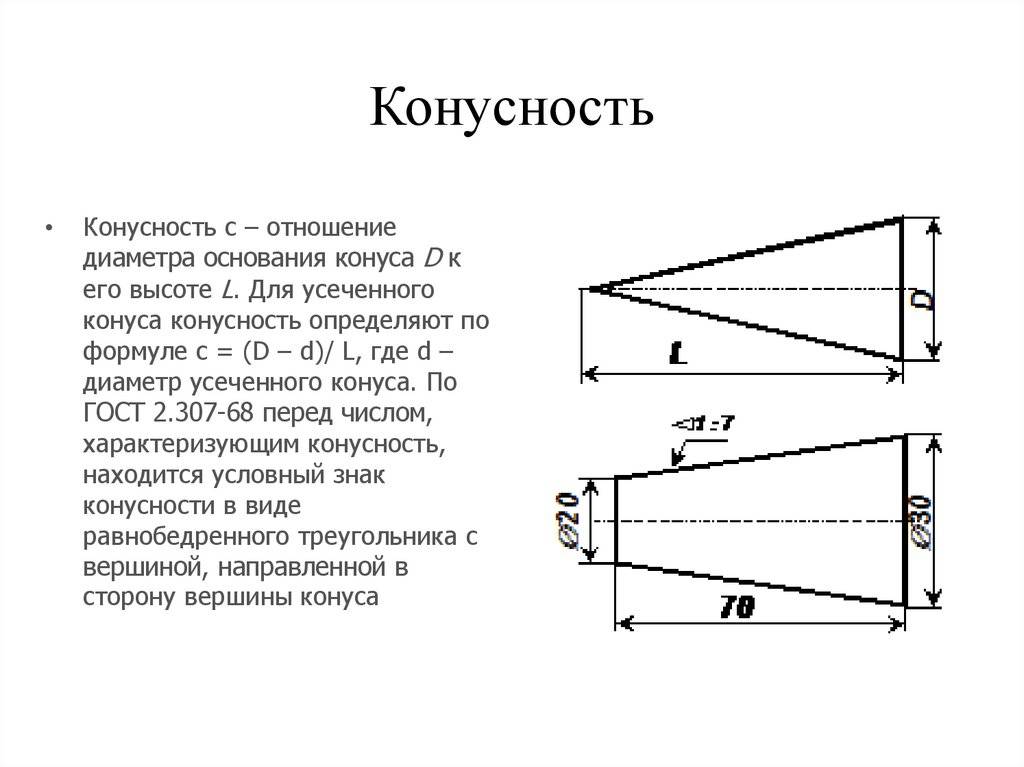
Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем

Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

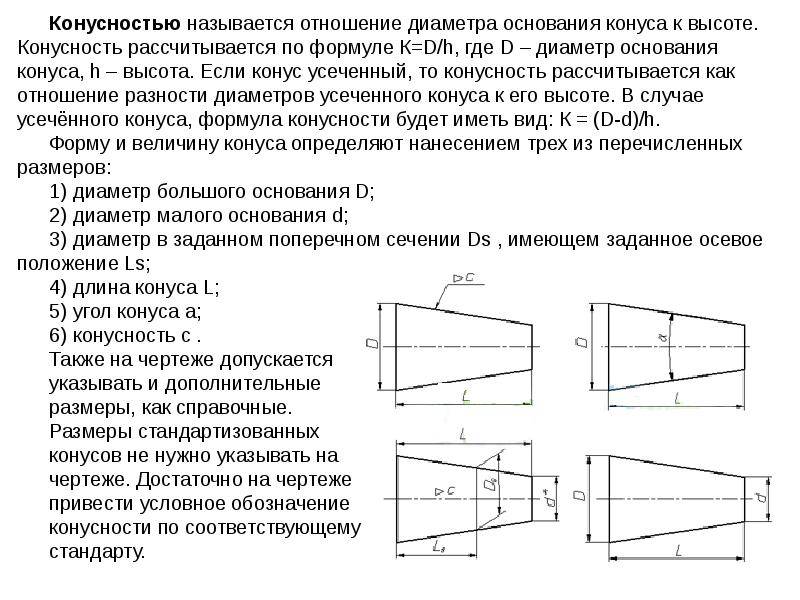
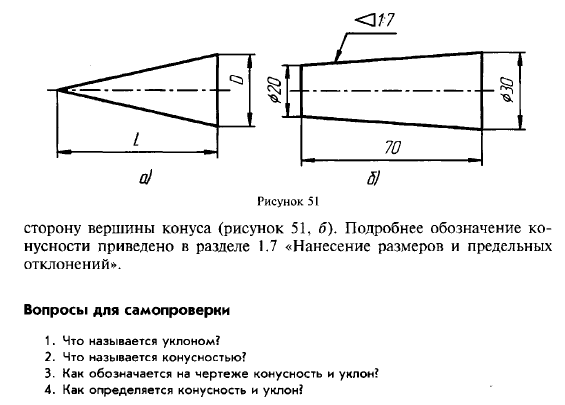
1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Совет 3 Как вычислить уклон

Если вам надобно вычислить уклон ската крыши либо уклон дороги, ваши действия будут различными, правда тезис расчета идентичен. Выбирать формулу для расчета уклон а следует в зависимости от того, в каких единицах необходимо получить итог.

Инструкция

1. В первую очередь реально либо мысленно постройте прямоугольный треугольник, в котором одной из сторон будет опущенный на землю перпендикуляр. Дабы возвести такой треугольник на участке земли либо дороге, воспользуйтесь нивелиром. Определите высоту в 2-х точках измеряемого объекта над ярусом моря, а также расстояние между ними.

2. Если надобно обнаружить уклон небольшого объекта, расположенного на земле, возьмите ровную доску либо и, применяя уровнемер, расположите ее сурово горизонтально между двумя точками. В нижней точке под нее придется подложить подручные средства, скажем, кирпичи. Померяйте рулеткой длину доски и высоту кирпичей.

3. Дабы обнаружить уклон ската крыши, зайдите на чердак и от определенной точки ската опустите вниз нить с грузом, до самого пола. Измерьте длину нити и расстояние от опущенного груза до пересечения ската с полом чердака. Методы измерения могут быть самыми различными, вплотную до фотографирования объекта и измерения сторон на фотографии – ваша цель при этом узнать длину 2-х катетов в полученном прямоугольном треугольнике.

4. Если у вас есть довольно подробная карта физическая карта местности, посчитайте уклон с ее подмогой. Для этого подметьте крайние точки и посмотрите, какие обозначения высоты там подмечены, обнаружьте между ними разницу. Измерьте расстояния между точками и при помощи указанного масштаба посчитайте настоящее расстояние

Обратите внимание, все расстояние обязаны быть измерены в одних и тех же единицах, скажем, только в метрах либо только в сантиметрах

5. Поделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам необходимо получить уклон в процентах, умножьте полученное число на 100%. Дабы получить уклон в промилле, умножьте итог деления на 1000‰.

6. Если вам нужно получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов итог – тангенс угла наклона. Посчитайте его арктангенс при помощи инженерного калькулятора (механического либо онлайн). В итоге вы получите значение уклон а в градусах.

Как считается уклон в процентах?

Уклон

– это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i. Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получитьуклон в процентах , умножьте полученное число на 100%.

Интересные материалы:

Когда выделяется переходное молоко? Когда выйдет Я никогда не? Когда выйдет iPad Air 4? Когда выйдет Кибертрак? Когда выйдет новая часть God of War? Когда выйдет новая модель iPad? Когда выйдет shadowlands? Когда выпустят Tesla Cybertruck? Когда вырабатывается хгч после имплантации? Когда вырабатывается пролактин при ГВ?

Обозначение конусности на чертеже

При разработке техдокументации должны предусматриваться все установленные нормы, так как в другом случае она не используют в последующем

Анализируя обозначение конусности на чертежах необходимо уделять свое внимание следующим моментам:

1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный критерий. В случае конуса их может быть несколько, а изменение критерия происходит медленно, не ступенчато. В основном, у аналогичной фигуры имеется больший диаметр, а еще переходной в случае наличия ступеньки.
2. Наноситься диаметр меньшего основания. Меньшее основание в ответе за образование необходимого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим Основанием считается критерием длины.
4. На основании выстроенного изображения устанавливается угол. В основном, для этого проводятся необходимые расчеты. В случае определения размера по нанесённому изображению при использовании специализированного прибора для измерений значительно уменьшается точность. Второй метод используется в случае создания чертежа для изготовления неответственных деталей.

Самое простое обозначение конусности учитывает также отображения дополнительных размеров, например, справочную. В большинстве случаев применяется символ конусности, который дает возможность сразу понят о разности диаметров.

Выделяют достаточно очень много самых разных параметров, которые затрагивают определения конусности. К свойствам отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проходит в зависимости от сфере использования чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особенную группу выделяют понятие нормальной конусности. Она варьирует в конкретном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Аналогичные критерии характерны большинству изделий, которые используются во время сборки самых разных механизмов. При этом выдерживать аналогичные значения значительно проще при использовании токарного оборудования. Однако, если понадобится могут выдерживаться и неточные углы, все будет зависеть от определенного случая.
3. При начертании ключевых размеров применяется чертежный шрифт. Он отличается неограниченным количеством свойств, которые должны предусматриваться. Для правильного отображения применяется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Характерности отображения в большинстве случаев зависит от того, какой чертеж. В большинстве случаев наноситься очень много самых разных размеров, что значительно затрудняет нанесение конусности. Собственно поэтому предусматривается возможность применения нескольких самых разных методов отображения аналогичной информации.

На чертеже рассматриваемый критерий отмечается в виде треугольника. При этом требуется цифровое значение, какое может рассчитываться при использовании самых разных формул.

Трубная цилиндрическая резьба

1. Единица измерений параметров — дюйм.
2. Направление будет левым.
3. Класс точности: Класс А в этом случае повышен, а класс В средний.

Почему измерение происходит в дюймах

Дюймовые размеры пришли к нам от западных производителей, так как требования действующего на постсоветском пространстве ГОСТа сформулированы на базе особой резьбы BSW (British Standart Whitworth либо резьба Витворта). Инженер-конструктор Джозеф Фитворт (1803−1887 год) изобрёл в далёком 1841 году и продемонстрировал такой же винтовой профиль для соединений разъёмного типа, и демонстрировал его как совершенно универсальный, надёжный, а также комфортный для использования.

Такой тип осуществления резьбы применяется как в простых трубах, так и в их элементах и соединениях: контргайках, муфтах, угольниках, тройниках.

В сечении профиля можно увидеть равнобедренный треугольник с общим углом в 55 градусов и закруглениями на вершинах и в самих впадинах контура, которые используются для более высокого герметичного соединения.

Нарезка резьбовых соединений должна осуществляться на размере до 6. Все трубы создаются крупными, для особой надёжности и предотвращения процесса разрыва трубы в соединениях стоит фиксировать дополнительной сваркой.

Условные обозначения в стандарте.

1. Международная: G.
2. Япония: PF.
3. Англия: BSPP.

Указания буквы G, а также диаметр отверстия в проходе будут указываться в виде дюймов. Наружный диаметр непосредственно резьбы в обозначении найти нельзя.

Размеры резьбы трубной дюймовой

G ½ — трубы в виде цилиндра наружного типа, внутренний диаметр отверстия равен ½. Наружный диаметр у такой трубы будет равняться 20,995 мм, число шагов по длине — 25,4 мм, что значит около 14 шагов.

Например:

1. G ½ -В— резьба трубная цилиндрическая, внутренний диаметр отверстия ½ дюйма, класс точности трубы совпадает с отметкой В.
2. G1 ½ LH-B— труба цилиндрического типа, внутренний диаметр отверстия доходит до ½, класс точности В, левая.

Для внутренней цилиндрической трубы стоит использовать отверстие, которое будет полностью соответствовать параметрам.

Как быстро найти шаг в трубе

Можно рассмотреть дополнительные фотографии с англоязычных сайтов, которые смогут наглядно продемонстрировать методику использования и построения конструкции. Трубочная резьба характеризуется в большинстве случаев не общим размером между вершинами профиля, а числом общих витков на 1 дюйм вдоль всей оси поверхности. При помощи простой рулетки, а также линейки прикладываем, отмеряем один дюйм (25,4 мм) и визуально высчитываем количество шагов.

Будет намного проще, если в вашем ящике с инструментами будет находиться резьбомер для дюймового отмера. Таким прибором довольно просто проводить все измерения, но стоит помнить о том, что резьба может различаться углами вершин — 55 и 60 градусов.

Коническая трубная резьба ГОСТ 6211081

Единица измерения всех параметров в этом случае — дюйм.

Форма такой трубы будет соответствовать профилю трубной цилиндрической вырезки с общим углом в 55 градусов Цельсия.

Главные обозначения:

1. Международная — R
2. Япония — PT.
3. Великобритания BSPT.

Для этого стоит указывать букву R и общий номинальный диаметр Dy. Обозначение в виде буквы характеризует наружный тип резьбы, Rc внутренний, а Rp — внутренний цилиндрический. По такому же аналогу с цилиндрической трубой для левой резьбы стоит применять LH.

Примеры:

R1 ½ -это наружная труба конической вырезки, номинальный диаметр которой равен Dy ½ дюйма.

R1 ½ LH — это наружная коническая труба, номинальный диаметр которой Dy будет равняться ½ дюйма.

1. Дюймовая вырезка конической формы по ГОСТу 6111−52.
2. Единица измерения в этом случае — также дюйм.
3. Происходит его изготовление на поверхности с конусностью 1:16.

Обладает общим углом профиля около 60 градусов. Используется в изготовлении трубопроводов (водяных, воздушных, а также топливных) машин и станков с невысоким давлением при работе. Применение такого вида соединений включает в себя особую герметичность и стопорение резьбы без воздействия дополнительных подручных средств (льняных нитей, а также пряжи с суриком).

Главные обозначения

Первой в названии имеется буква К, а после идёт слово ГОСТ.

Пример: К: ½ ГОСТ 6111–52 .

Расшифровывается такая надпись так: резьба коническая дюймовая с наружным, а также внутренним диаметром в основной плоскости, примерно равной наружному либо внутреннему разъёму трубы цилиндрического типа G ½.

Метрически конический тип вырезки. По ГОСт у 25229 -82.

Единицей измерения в этот раз выступает мм.

Процесс создания трубы происходит на поверхностях с общей конусностью в 1:16.

Применяется во время соединения трубопроводов. Угол в самой вершине витка будет доходить до 60. Главная плоскость смещена, если смотреть на торец.