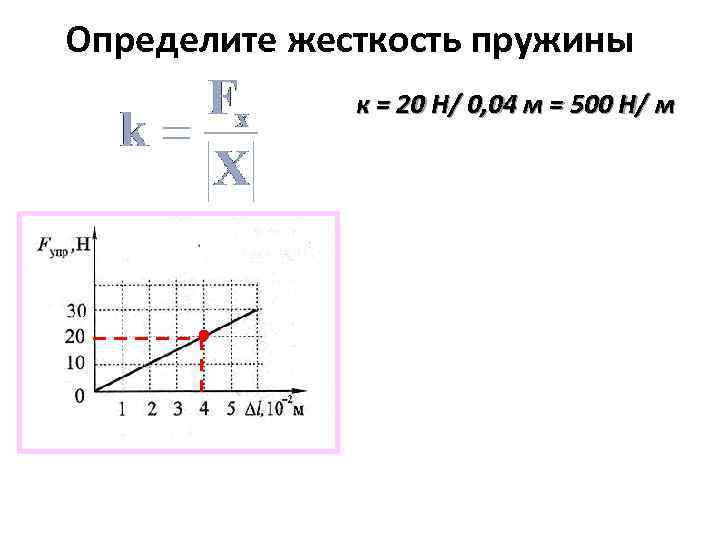
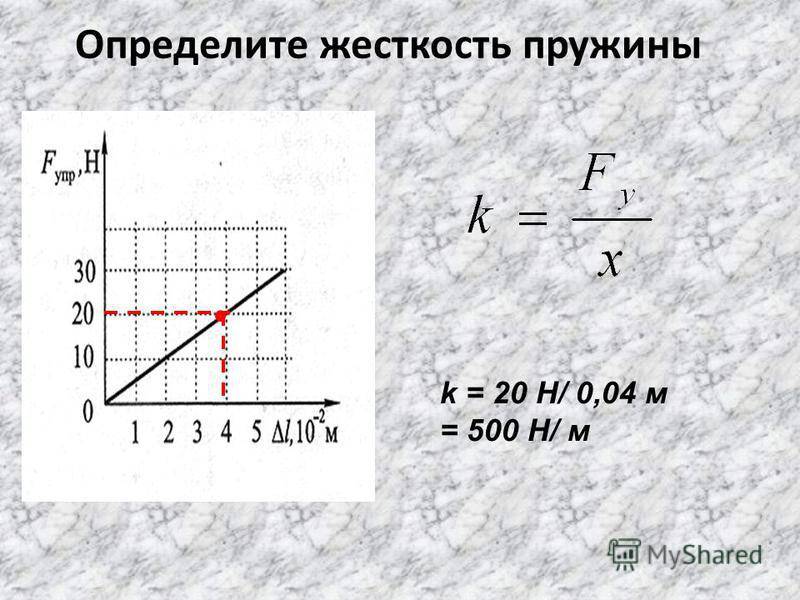
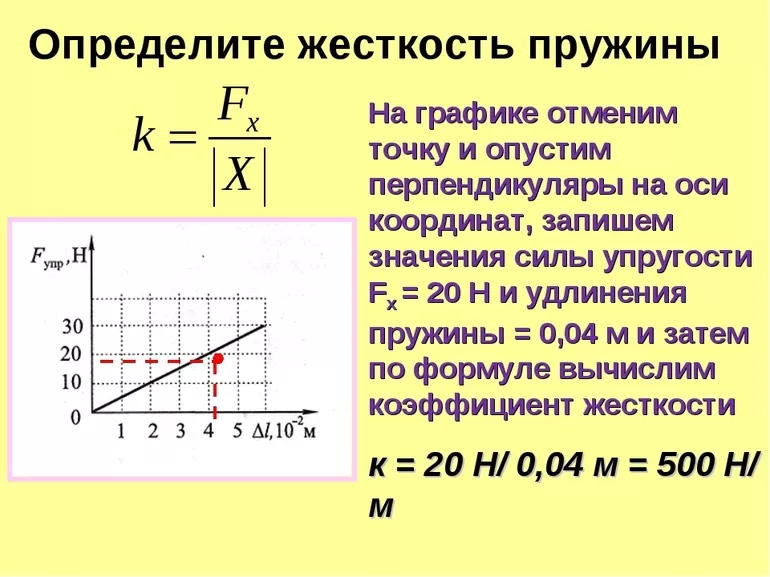
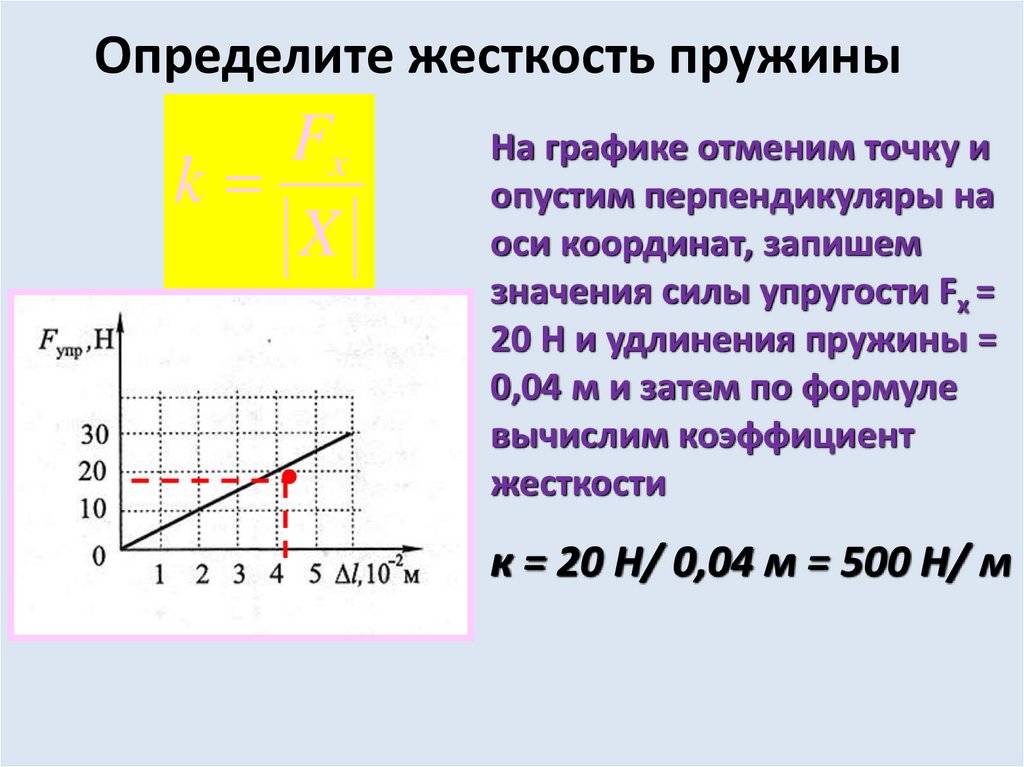
Коэффициент жесткости пружины: определение, формулы, измерение

Пружина постоянного усилия:

Пружина постоянной силы устанавливается на барабан, оборачивая его вокруг барабана. Пружина должна быть плотно обернута. Затем свободный конец пружины прилагается к силе нагрузки, например, при использовании противовеса или наоборот.

Диаметр барабана должен быть больше внутреннего диаметра.
Диапазон: 10-20% диаметра барабана> Внутренний диаметр.
На барабане при крайнем растяжении должна быть полуторная пружина.
Полоса будет нестабильной на больших расширениях, поэтому рекомендуется использовать ее меньшего размера.
Диаметр шкива должен быть больше исходного диаметра.

Физика

3.4. Механическая энергия

3.4.2. Потенциальная энергия

Потенциальная энергия — это механическая энергия системы тел, определяемая их (или частей одного тела) взаимным расположением.

Потенциальная энергия деформированной пружины

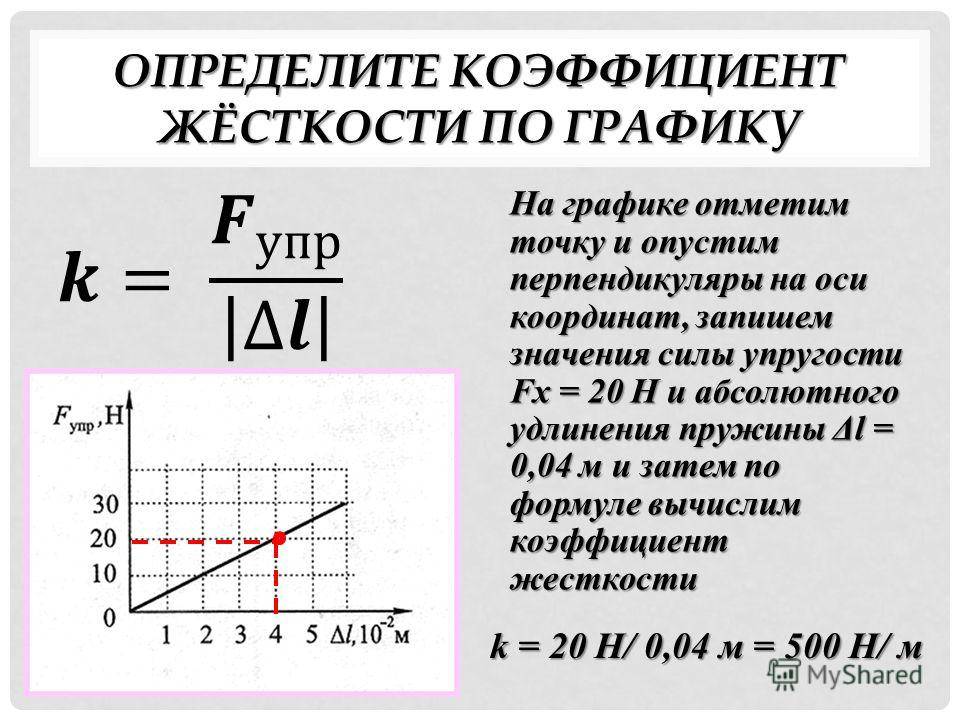
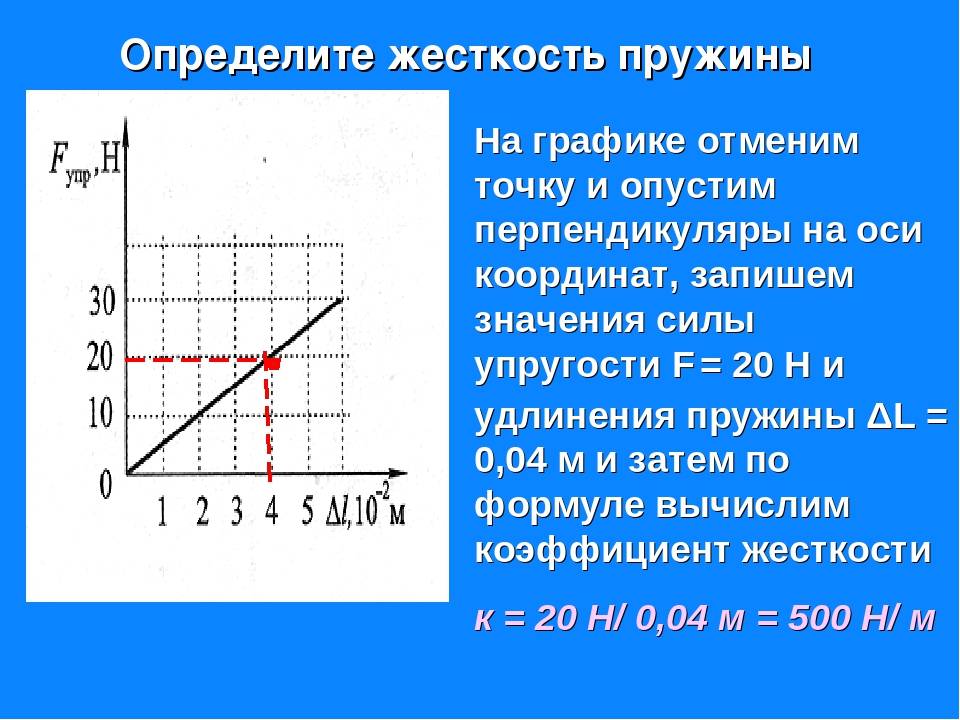
Деформированная пружина (сжатая или растянутая) (рис. 3.7) обладает потенциальной энергией, которая определяется формулой

W p = k ( Δ l ) 2 2 ,

где k — коэффициент жесткости (упругости) пружины; ∆l — величина абсолютной деформации пружины (удлинения или сжатия).

Рис. 3.7

Потенциальная энергия недеформированной пружины равна нулю.

Следует отметить, что потенциальная энергия деформированной пружины всегда является положительной величиной.

В Международной системе единиц потенциальная энергия деформированной пружины измеряется в джоулях (1 Дж).

Потенциальная энергия взаимодействия тела и Земли

Тело, расположенное на расстоянии h над поверхностью Земли (или под ее поверхностью), обладает потенциальной энергией, которая определяется формулой

Wp = mgh + C,

где m — масса тела; g — модуль ускорения свободного падения.

Выбор константы C является условным и зависит от конкретной задачи; часто указанную константу выбирают таким образом, чтобы на поверхности планеты потенциальная энергия взаимодействия тела и планеты обращалась в ноль.

Следует отметить, что потенциальная энергия взаимодействия тела и Земли может быть как положительной, так и отрицательной величиной.

В Международной системе единиц потенциальная энергия тела, поднятого на некоторую высоту относительно поверхности Земли, измеряется в джоулях (1 Дж).

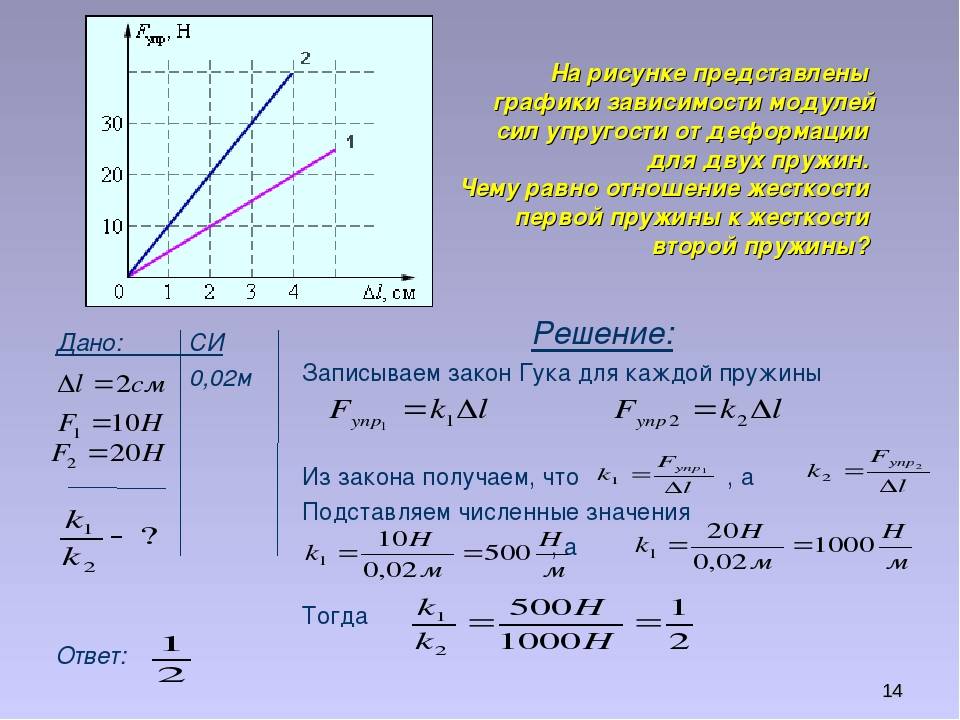
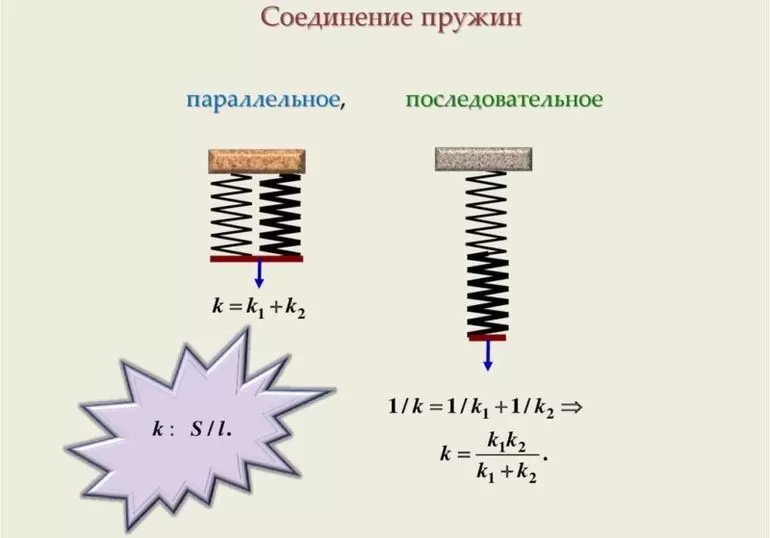
Пример 26. Две пружины с одинаковыми коэффициентами жесткости по 1,0 кН/м соединили последовательно. Составную пружину растянули на 10 см. Во сколько раз увеличится потенциальная энергия деформации, если эти же пружины соединить параллельно, а величину деформации системы оставить прежней? Рассчитать потенциальную энергию пружин при последовательном и параллельном соединении, считая деформацию составной пружины одинаковой и равной 10 см.

Решение. Потенциальная энергия составной пружины определяется формулой

W p = k общ ( Δ l ) 2 2 ,

где kобщ — общий коэффициент жесткости составной пружины; ∆l — величина деформации пружины.

Коэффициент жесткости составной пружины определяется по-разному:

для N одинаковых пружин, соединенных последовательно,

k общ 1 = k 0 N ;

для N одинаковых пружин, соединенных параллельно,

kобщ2 = Nk0,

где k0 — коэффициент жесткости одной пружины; N = 2 — количество соединенных пружин.

Потенциальная энергия составной пружины вычисляется по формулам:

для N одинаковых пружин, соединенных последовательно,

W p 1 = k общ 1 ( Δ l ) 2 2 = k 0 ( Δ l ) 2 2 N ;

для N одинаковых пружин, соединенных параллельно,

W p 2 = k общ 2 ( Δ l ) 2 2 = N k 0 ( Δ l ) 2 2 .

Отношение потенциальных энергий

W p 1 W p 2 = k 0 ( Δ l ) 2 2 N 2 N k 0 ( Δ l ) 2 = 1 N 2

определяется только количеством пружин и не зависит от деформации составной пружины.

Рассчитаем потенциальную энергию составной пружины, состоящей из двух одинаковых пружин,

соединенных последовательно:

W p 1 = k 0 ( Δ l ) 2 2 N = 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 ⋅ 2 = 2,5 Дж;

соединенных параллельно:

W p 2 = N k 0 ( Δ l ) 2 2 = 2 ⋅ 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 = 10 Дж.

Отношение указанных потенциальных энергий равно

W p 1 W p 2 = 1 N 2 = 1 2 2 = 4 .

Следовательно, при одинаковой деформации потенциальная энергия пружины, составленной из двух одинаковых параллельно соединенных пружин, в 4 раза больше потенциальной энергии пружины, составленной из двух одинаковых последовательно соединенных пружин.

Пример 27. Какой энергией обладает тело массой 500 г на вершине горы относительно дна озера, находящегося у подножия горы? Высота горы составляет 1,50 км, а глубина озера 250 м.

Решение. Потенциальная энергия тела, поднятого на некоторую высоту, определяется формулой

Wp = mgh,

где m — масса тела; g — модуль ускорения свободного падения; h — высота, на которую поднято тело над определенным уровнем, характеризуемым нулевым значением потенциальной энергии.

Выберем нулевой уровень потенциальной энергии (Wp = 0) на дне озера так, как показано на рисунке.

Тогда высота, на которую поднято тело над указанным уровнем, является суммой:

h = h2 + h2,

где h2 = 1,50 км — высота горы; h2 = 250 м — глубина озера.

Потенциальная энергия тела относительно дна озера определяется выражением

Wp = mg(h2 + h2).

Расчет дает значение:

W p = 500 ⋅ 10 − 3 ⋅ 10 ⋅ ( 1,50 + 0,25 ) ⋅ 10 3 = 8,75 ⋅ 10 3 Дж = 8,75 кДж.

Вычисляем энергию простого гармонического движения

В простом гармоническом движении периодически происходит увеличение и уменьшение кинетической энергии, например груза на пружине. Ясно, что кинетическая энергия груза не пропадает, а преобразуется в энергию сжатой или растянутой пружины. Эта энергия называется упругой потенциальной энергией пружины. Сколько энергии запасено в сжатой или растянутой пружине?

Попробуем вычислить ее с помощью простых соображений. Как известно, работа $ A $ силы $ F $ при перемещении на расстояние $ s $ равна:

При сжатии или растяжении пружины сила $ F $ меняется линейно с расстоянием, поэтому работу этой силы по сжатию или растяжению пружины на расстояние $ s $ можно представить как произведение средней силы $ \overline{F} $ на перемещение $ s $:

Средняя $ \overline{F} $ сила определяется как:

где $ F_1=-kx_1 $ — это сила упругости в точке с координатой $ x_1 $, a $ F_2=-kx_2 $ — сила упругости в точке с координатой $ x_2 $. При этом перемещение $ s $ будет равно:

Подставляя выражения для $ s $ и $ \overline{F} $ в формулу работы, получим:

Члены $ \frac{kx^2_1}{2} $ и $ \frac{kx^2_2}{2} $ выражают упругую потенциальную энергию пружины $ E_{у1} $ и $ E_{у2} $ в точках с координатами $ x_1 $ и $ x_2 $, соответственно. Таким образом, работа силы упругости равна изменению упругой потенциальной энергии пружины:

Рассмотрим простой пример. Насколько возрастет упругая потенциальная энергия пружины с коэффициентом упругости 1,0·10-2 Н/м при сжатии ее на 10 см? Подставляя значения в формулу

получим:

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями “цилиндров”, диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние “цилиндры” при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

$k = \frac{r^4}{4R^3} \cdot \frac{G}{n}$,

$R$ – радиус цилиндра пружины,
$n$ – количество витков проволоки радиуса $r$,
$G$ – коэффициент, зависящий от материала.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

$k = \frac{(10^{-3})^4}{4 \cdot (2 \cdot 10^{-2})^3} \cdot \frac{8 \cdot 10^{10}}{25} = \frac{8 \cdot 10^{-2}}{10^2 \cdot 2^3 \cdot 10^{-6}} = 100$

Ответ: $100 \frac{Н}{м}$

При воздействии внешних сил тела способны приобретать ускорения или деформироваться. Деформацией называют изменение размеров и (или) формы тела. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

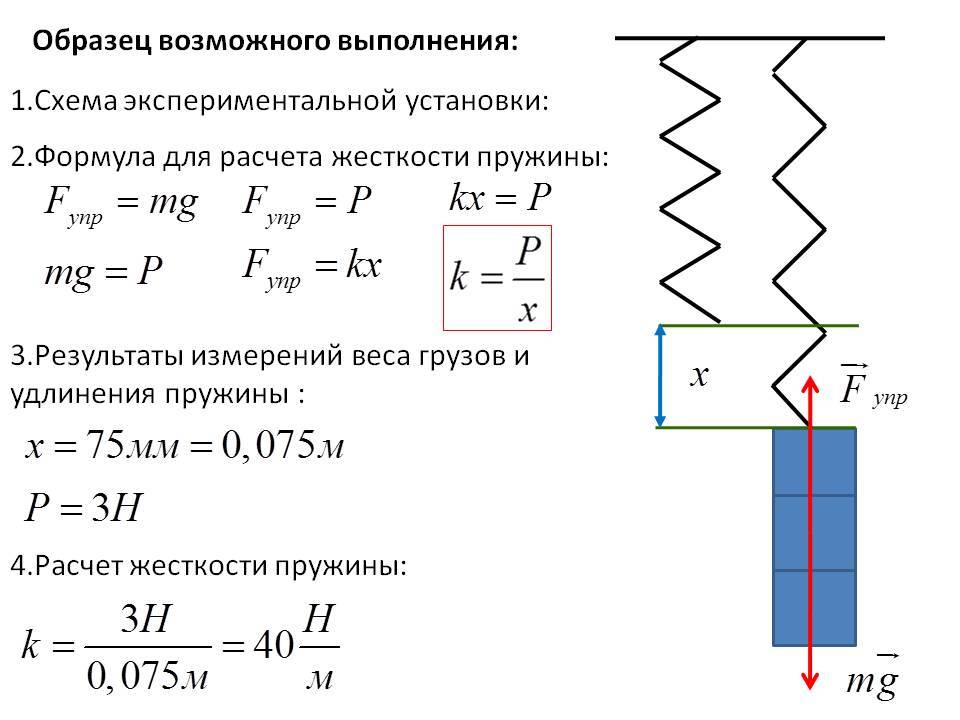
Пусть на пружину на рис.1 действует растягивающая сила, направленная вертикально вниз.

При воздействии деформирующей силы ($\overline{F}$) длина пружины увеличивается. В пружине возникает сила упругости (${\overline{F}}_u$), которая уравновешивает деформирующую силу. Если деформация небольшая и упругая, то удлинение пружины ($\Delta l$) пропорционально деформирующей силе:

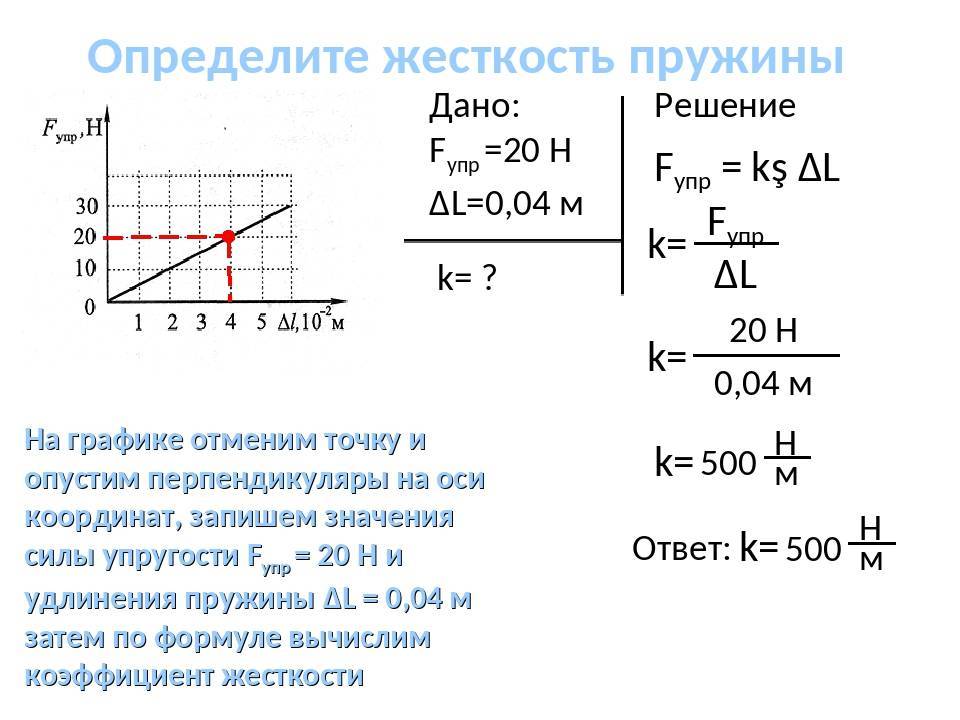
где в качестве коэффициента пропорциональности выступает жесткость пружины $k$. Коэффициент $k$ называют также коэффициентом упругости, коэффициентом жесткости. Жесткость (как свойство) характеризует упругие свойства тела, подвергаемого деформации – это возможность тела оказывать противодействие внешней силе, сохранять свои геометрические параметры. Коэффициент жесткости является основной характеристикой жесткости.

Коэффициент жесткости пружины зависит от материала, из которого изготовлена пружина, ее геометрических характеристик. Так, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси вычисляется при помощи формулы:

где $G$ -модуль сдвига (величина зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.

Причины поломки пружины

Существует пять основных причин, по которым задние и/или передние пружины полностью или частично выходят из строя.

Усталость металла и износ пружин. Происходит это по естественным причинам со временем. Металл в процессе эксплуатации становится мягче и податливее, соответственно, и пружина становится мягче. А также при столкновении витков пружины ржавеют и появляются микротрещины. Особенно вредно для прутков сильные удары возникающие при наезде машины на большой скорости на выбоину или кочку.
Постоянное трение витков ослабленной либо сильно загруженной пружины между собой. По этой причине снижается жесткость пружины, а поверхность самих витков становится не круглая, как была изначально, а имеющая выработанную плоскость. Соответственно, по этой причине пруток становится тоньше, а значит и пружина слабее.
Перегрузка автомобиля и езда на нем в таком состоянии на большой скорости по неровностям или расстояния. В таких условиях страдают все элементы подвески, в том числе, пружины.
Коррозия металла пружин. Это очень частая причина, по которой пружины выходят из строя. Со временем краска на их поверхности облущивается, а вода и дорожные реагенты делают свое дело. Интересно, что если коррозия «съела» на 10-мм проволоке пружины слой всего лишь 0,15 мм, то сечение указанной проволоки уменьшается аж на 6%!
Установка неподходящей пружины. В частности, это может произойти по причине неправильного подбора детали. Другой вариант — заводской брак. Зачастую бывает так, что в одной упаковке помещаются пружины с разной жесткостью.

Какие бывают типы пружин

В первую очередь их принято делить на предназначенные для работы в режиме растягивания и предназначенные для работы в режиме сжатия.

Пружины растяжения при действии на них полезной нагрузки растягиваются. Они не нуждаются в жёстком захвате и, как правило, имеют нулевой шаг, т. е. витки у них прилегают вплотную друг к другу. В обычной жизни подобные изделия большинство людей может заметить, проходя через двери с механическим механизмом закрытия или при пользовании пружинными весами. В технике пружины растяжения используются для соединения элементов, положение которых меняется при их работе. В качестве примера можно привести завес рычагов.

Пружины сжатия под нагрузкой по длине уменьшаются. Для правильной работы их концы должны быть жёстко зафиксированы. Витки проволоки в свободном состоянии не касаются друг друга, т.к. им необходим некоторый промежуток, чтобы под внешней нагрузкой было куда перемещаться. В качестве примера использования таких изделий можно привести пружину в шариковой ручке или автомобильную подвеску.

В технике широкое применение находят и другие типы пружин: пружины кручения (в точных весах), плоские спиральные (как заводные в часах), плоские (в автомобильных рессорах), тарельчатые (в грузовых весах). В некотором роде пружинами можно назвать некоторые изделия из резины и из других полимерных эластичных материалов. Все они работают по одной и той же схеме – запасают кинетическую энергию в виде энергии упругости, а затем, когда нагрузка ослабнет или вовсе перестанет действовать, её возвращают.

Применение и разновидности пружин

Пружина является упругим изделием, что обеспечивает трансформацию нарастающих двигательных импульсов к приборным и механизменным составляющим собственного звена. Встречается устройство во многих изделиях как в бытовых приборах, так и в производственных элементах. А степень надежности работы механизмов на производстве зависит от коэффициента пружинной жесткости. Эту величину следует соизмерять с усилием, приложенным к пружине, что определяет ее сжатие или растяжение. Пружинное вытяжение зависит от свойств металла, который ее составляет, а не от коэффициента упругости.

Пружинный элемент имеет разнообразные структуры. Все зависит от того, для чего он предназначен. По деформационным особенностям и структурным характеристикам пружина бывает:

спиральной;
канонической;
цилиндрической.

Коэффициентный показатель жесткости определенного элемента зависит от способа деформационной передачи. Параметры деформации подразделяют все механизмы на такие:

ввинчивающиеся;
крутящиеся;
изогнутые;
растягивающиеся.

При одновременном применении нескольких пружинных механизмов в одном изделии жесткостный показатель будет обусловлен крепежным элементом. Если все соединено параллельным креплением, то показатель будет расти, а последовательное крепление предусматривает уменьшение.

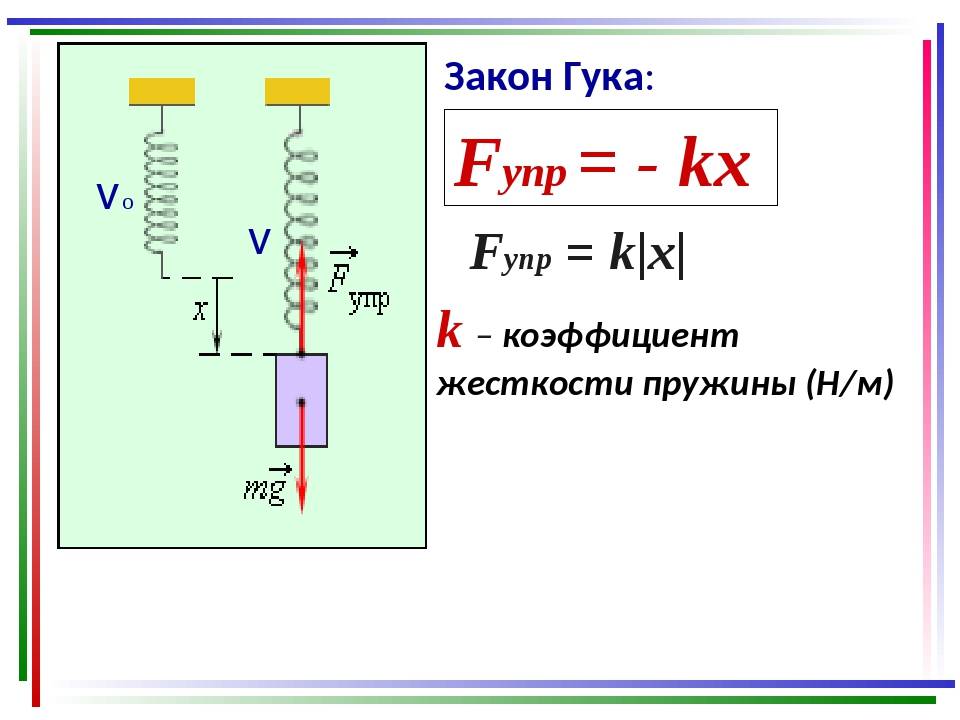
Сила упругости: Закон Гука

Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.

Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Закон Гука

Fупр = kx

Fупр — сила упругости k — коэффициент жесткости [Н/м] х — изменение длины (деформация)

Важно раз

Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Важно два

Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.

СИ — международная система единиц.

«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

m = 300 г = 0,3 кг

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

F = mg = 0,3*10 = 3 Н.

Тогда из Закона Гука выразим модуль удлинения лески:

F = kx

Выражаем модуль удлинения:

x = F/k

Подставим числа, жесткость лески при этом выражаем в Ньютонах:

x=3/(0,3 * 1000)=0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

Свойства пружин подвески

Когда торсионы на транспортных средствах заменили на пружины, улучшилась управляемость, . Пружины поддерживают клиренс автомобиля, уменьшая вибрации и удары во время движения транспортного средства.

Чтобы езда была комфортной, необходимо правильно подобрать детали. Если теххарактеристики будут неподходящими, то положительные свойства подвески будут сведены к нулю

Потому важно учитывать следующие параметры:

диаметр — его увеличение влияет на жёсткость;
количество витков — при увеличении жёсткость снижается;
форма.

Зачастую автовладельцы стремятся установить в подвеску более жёсткие детали. Это способствует увеличению чувствительности рулевого колеса к управлению водителем, но сцепление с дорогой ухудшается.

Любители спортивного стиля езды считают, что, напротив, лучше ставить детали с пониженной жёсткостью. Однако такая подвеска может создать проблемы на просёлочных дорогах.

Давайте рассмотрим подробнее, какие пружины лучше установить на ВАЗ.

Отличия пружин подвески и их маркировка

Основным идентификационным параметром любой пружины служит ее наружный диаметр. Производители не могут его самопроизвольно изменить, так как этот размер определяется конструктивными особенностями самого автомобиля. Все остальные параметры могут быть абсолютно различными. Так производители могут:

изменить диаметр прута, из которого она изготавливается и даже использовать прут, имеющий диаметр переменного значения;
изготавливать пружины одинаковой высоты, но различной жесткости;
изменить межвитковое расстояние и количество витков, сохраняя при этом жесткость.

Статья в тему: Как зарегистрироваться на экзамен в ГИБДД через госуслуги? Поэтому на заводах перед установкой проводят контроль статистической нагрузки. Проводится такая операция следующим образом: измеряют высоту пружины, сжав ее с определенным усилием. Так как для каждой конкретной модели автомобиля высота в сжатом состоянии регламентирована полем допуска, то детали, не попавшие в это поле, выбраковываются.

Пружины, попавшие в границы верхнего поля допуска относят к классу А (длинные), а в категорию В (короткие) попадают те, что имеют высоту в пределах нижнего поля допуска. Далее пружины одного класса маркируют краской, причем цвет маркировки зависит от модели автомобиля, на котором они должны быть установлены.

Пружины класса А автомобилей ВАЗ маркируют по цвету желтой, белой, коричневой и оранжевой красками.
Вид В также маркируют по цвету, но зеленой, голубой, синей и черной красками.

Маркировка по цвету наносится на внешнюю сторону витков в виде цветной полоски. Обилие цветов маркировочной краски объясняется тем, что с целью уменьшения влияния коррозии, они подвергают специальному покрытию (хлоркаучуковая эмаль или защитное эпоксидное покрытие), которое также бывает разного цвета (черное, серое, синее, белое, голубое) и определяет как модель автомобиля, так и назначение пружины (передняя или задняя). Причем на заводах, выпускающих различные модели ВАЗ и «Лада», передние элементы окрашены, как правило, в черный цвет. Исключение составляют только пружины с переменным межвитковым расстоянием (шагом) — они окрашиваются в голубой цвет.

Статья в тему: Самостоятельное приготовление электролита для АКБ

Расчет пружины сжатия из проволоки прямоугольного сечения

Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.

Основным отличием в расчете, как вы уже догадались, является определение жесткости витка (C 1 ) , задающей жесткость пружины (C ) в целом.

Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.

После выполнения расчета по программе выполняйте проверку касательных напряжений!!!

4. I =(D 1 B ) -1

5. При 1/3 Y =5,3942*(H B ) 2 -0,3572*(H /B )+0,5272

При 1 Y =5,4962*(H B ) (-1.715)

При 2H B Y =3 ,9286 *(H B ) (-1. 2339 )

6. При H B C 1 =(78500* H 4 )/(Y * (D 1 — B ) 3)

При H > B C 1 =(78500* B 4 )/(Y * (D 1 — B ) 3)

8. T nom =1,25*(F 2 C 1 )+H

9. T max =π*(D 1 — B )*tg (10 ° )

11. S 3 = T — H

12. F 3 = C 1 * S 3

14. N расч =(L 2 — H )/(H +F 3 C 1 — F 2 C 1 )

16. C = C 1 N

17. L 0 = N * T + H

18. L 3 = N * H + H

19. F 2 = C * L 0 — C * L 2

21. F 1 = C * L 0 — C * L 1

22. N 1 = N +1,5

23. A =arctg (T /(π *(D 1 — H )))

24. L разв =π* N 1 *(D 1 — H )/cos (A )

25. Q =H *B * L разв *7,85/10 6

Это интересно: Конденсатор для пуска электродвигателя, как рассчитать мощность — во всех подробностях

Понятие жесткости воды, формула расчета, единицы измерения, нормы в России

О том, что водопроводная вода слишком жесткая, приходиться слышать постоянно. Чем же измеряется «твердость» жидкости? И как рассчитывается жесткость воды.

На фото: «пострадавший» от солей жесткости нагревательный элемент

Если свести к минимуму научные рассуждения о совокупности свойств жидкости, то жесткостью воды можно считать суммарное количество растворенных солей щелочноземельных металлов (преимущественно кальция и магния). С химической точки зрения все двухвалентные катионы в той или иной степени способны связываться с анионами, образуя соли, способные выпадать в осадок. Однако на практике количество растворенного в воде стронция, бария и марганца сведено к минимуму, а алюминий и железо переходят в солевые комплексы только при определенном уровне кислотности среды (рН меньше 7), который в природе практически не встречается. Мы уже писали про то, как определить жесткость в домашних условиях.

Таблица 1. Катионы и анионы, обуславливающие жесткость

Катионы жесткости	Анионы жесткости
Кальций (Ca2+)	Гидрокарбонат (НСО₃—)
Магний (Mg2+)	Сульфат (SO₄2-)
Стронций (Sr2-)	Хлорид (Cl—)
Железо (Fe2+)	Нитрат (No₃—)
Марганец (Mn2+)	Силикат (Sio₃2-)

Формула жесткости воды

Формула позволяет рассчитать суммарное количество ионов кальция и магния в воде, используется для лабораторных исследований. В настоящее время выделяют несколько типов жесткости:

Карбонатная жесткость – количественное содержание в воде гидрокарбонатов и карбонатов магния и кальция (MgHCO3, CaHCO3). Данный тип загрязнителей легко устраняется при кипячении с образование угольной кислоты и осадка:

Некарбонатная (постоянная) жесткость обусловлена присутствием магниевых и кальциевых соединений сильных кислот (азотной, соляной, серной). При кипячении соли такого типа не распадаются.

Формула для расчета общей жесткости воды: H_общ=Н_карб+Н_некарб

Единицы измерения

Единицы измерения в России – градусы (°Ж), может быть выражена в объемной или массовой доле. 1 градус жесткости численно равен 0,5 мольной концентрации щелочноземельного элемента, выраженной в мг/куб. дм. (1°Ж=1 мг-экв/л.)

Единицы измерения в системе СИ – моль/куб.метр. Однако на практике чаще всего используют мг-экв./л. Концентрация, отнесенная к единице массы, оправдывает себя в тех случаях, когда необходим анализ воды в ином агрегатном состоянии (с измененной плотностью).

Для тех, кому химия на уроках давалась нелегко, следует повторить:

Один мг-экв/л соответствует 20,04 миллиграммам ионов Ca2+ или 12,16 миллиграммам ионов Mg2+ (отношение атомной массы и валентности элемента).

Нормы жесткости

По величине жесткости воду можно разделить на три категории:

— мягкая (до 2 °Ж),

— средней жесткости (2-10 °Ж),

— очень жесткая (более 10 °Ж).

Нормы жесткости в России не позволяют превышать 7 мг-экв/л. Согласно стандартам Евросоюза, ПДК общей жесткости воды не может быть больше 1,2 мг-экв/л. Путем несложных расчетов можно сделать вывод о том, что в Европе вода почти в 6 раз мягче, чем в России.

Таким образом, численно подтвержденная необходимость установки систем очистки в России уже не вызывает сомнений. Кроме того, согласно принятым во всем мире нормативам, употребляемая нашими соотечественниками вода, нуждается в многоступенчатом умягчении и глубокой фильтрации.

Теперь разберемся, как устранить чрезмерное содержание солей в воде:

— Обзорная статья про то, как уменьшить жесткость воды: способы;

— Умягчители воды

Виды;

— Магнитные

— Ионообменные

Используемая литература:

ГОСТ 2874—82
ГОСТ Р 52029-2003 | НАЦИОНАЛЬНЫЕ СТАНДАРТЫ
Химическая энциклопедия. — М.: Советская энциклопедия, 1990. Т. 2. С. 145.

Классификация

Различают несколько видов пружин:

Стандартные. Как правило, устанавливаются на заводе изготовителе транспортного средства, и обеспечивают его эксплуатацию в условиях паспортных параметров нагрузки.
Усиленные. Отличаются большей жесткостью и улучшают эксплуатационные характеристики транспортного средства во время движения по проселочным дорогам, или при транспортировании прицепа.
Повышающие. Способствуют увеличению клиренса и грузоподъемности.
Понижающие. Уменьшают клиренс и снижают высоту центра тяжести. Устанавливаются любителями динамического стиля вождения.

Все они, независимо от того, к какому виду относятся, имеют специфические особенности при изготовлении.

Коэффициент жесткости пружины