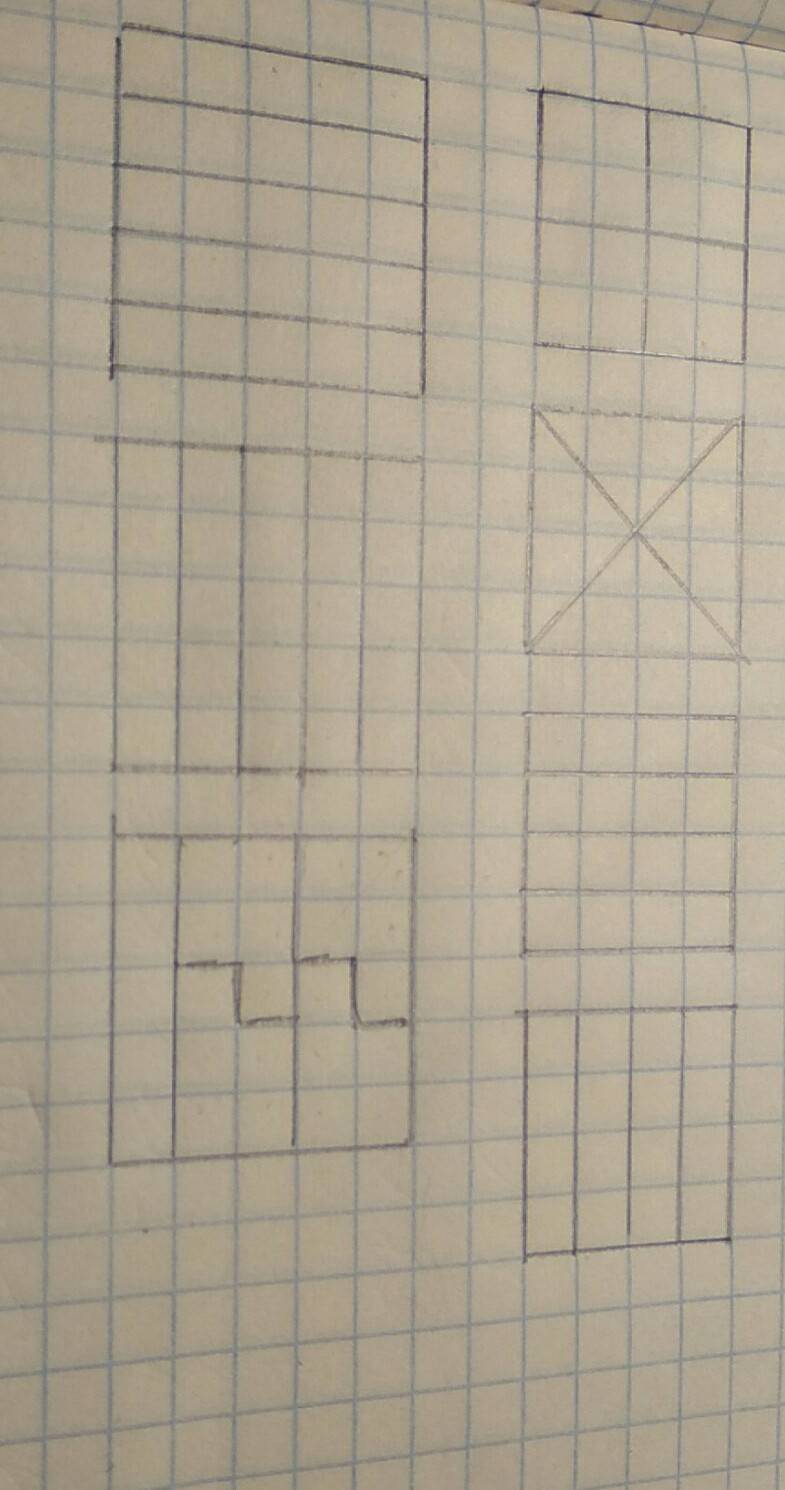Как разрезать квадрат на 4 равные части

Как нарезать круглый торт

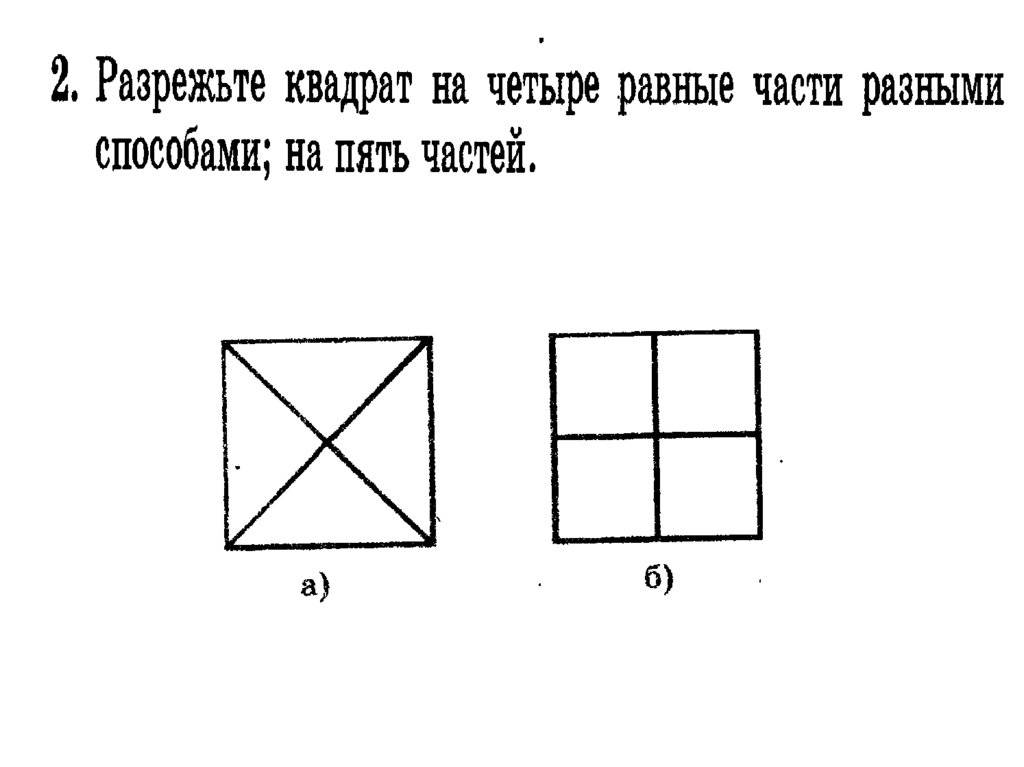
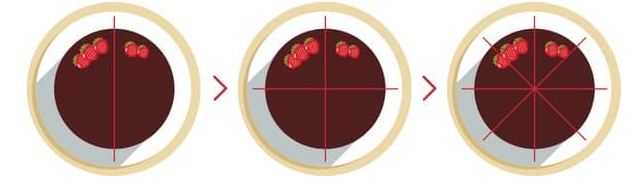
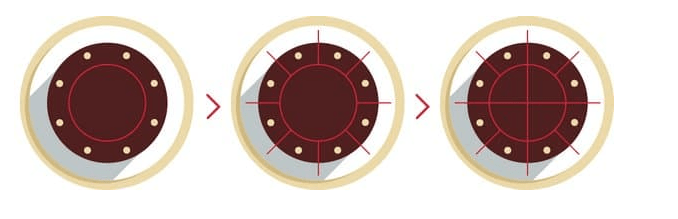
При подаче торта гостям важно разрезать торт на примерно одинаковые куски. Если торт круглый и гостей немного (до 8 человек), то сделать это можно классическим способом

Для этого сначала нужно разрезать торт пополам по вертикали и по горизонтали. Затем, оставшиеся четверти нужно разрезать на две равные части.

Если торт большого диаметра нужно разрезать на 12 и больше кусков, то можно воспользоваться методом «ромашка». Для этого вам понадобится тарелка с диаметром меньше, чем у торта. Тарелку кладут на поверхность торта, тем самым закрывая центр. Выступающую часть торта делят на равные части. 

Затем тарелку снимают и нарезают оставшуюся середину торта классическим способом. Если торт имеет очень большой диаметр, то может понадобится две или даже три тарелки разных диаметров. Их поочерёдно кладут на середину торта и нарезают нужное количество кусков.

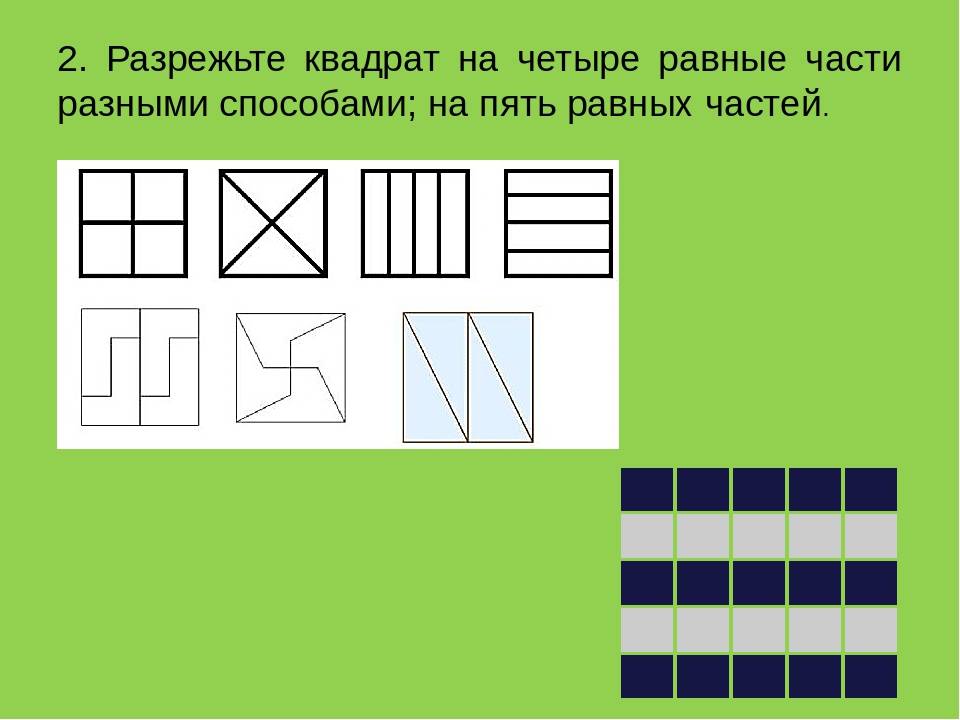
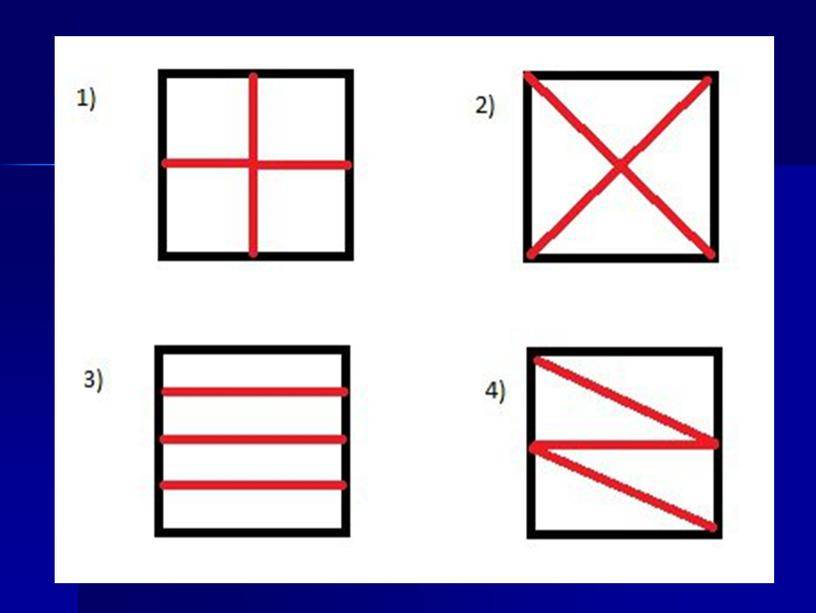
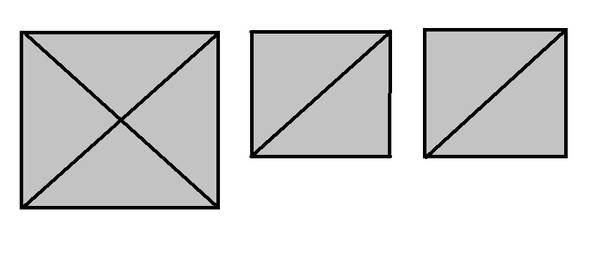
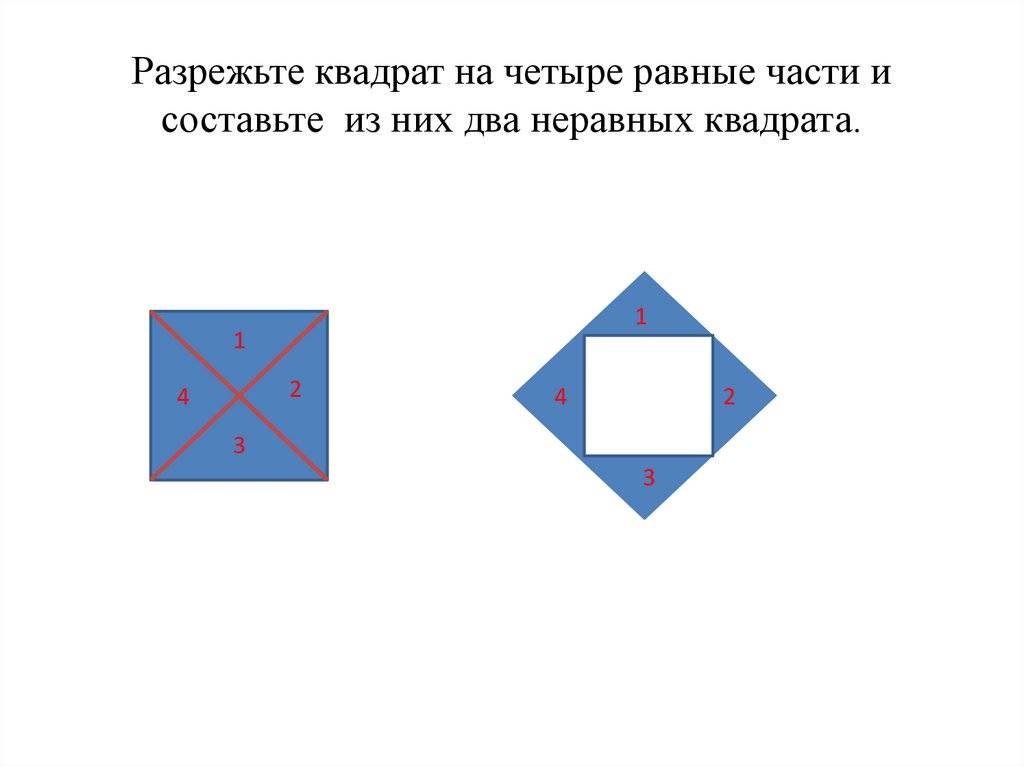
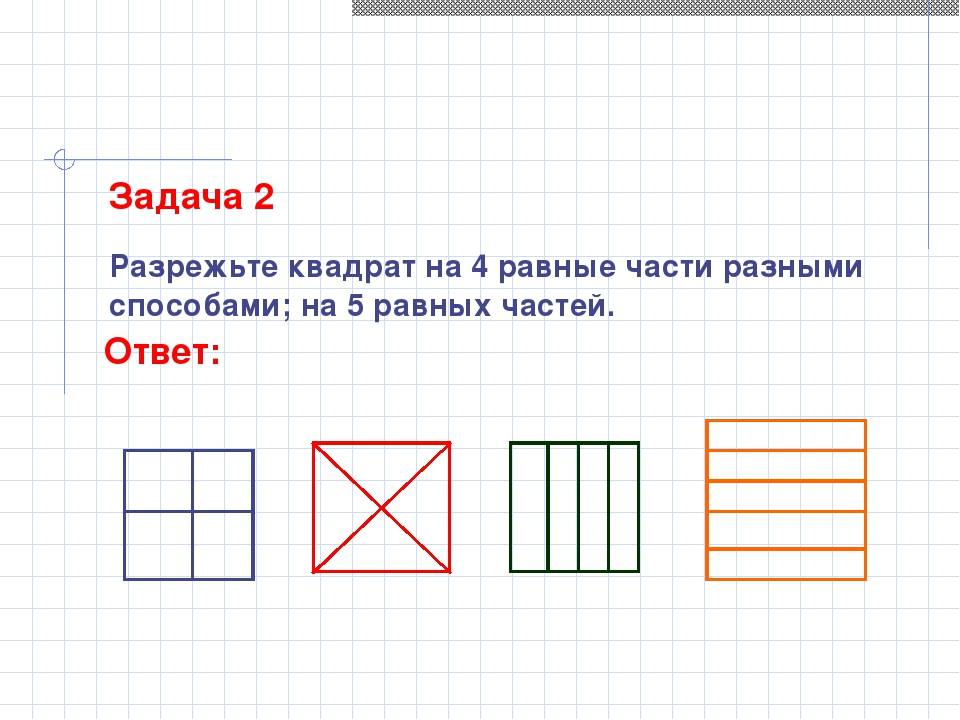
3 способа разрезать квадрат

Предисловие о Введение 7 §1 Складывание прямоугольника из квадратов и разрезание квадрата 12 §2 Графы и электрические цепи 34 § 3 Основная теорема 51 § 4 Дальнейшие задачи и результаты 67 1 Простые и составные разбиения прямоугольника и квадрата 67 2 Разбиения прямоугольников на квадраты и числа Фибоначчи 71 3 Оценки для числа квадратов, нЗ которые может быть разбит данный прямоугольник 75 4 Как разрезать поверхности цилиндра и конуса? 89 5 Как разрезать треугольник? 91 6 Как разрезать куб? 98 Некоторые нерешенные задачи 105 Литература 109

В 1965 г. в серии «Математическая библиотечка» были изданы две книги, посвященные так называемой «комбинаторной геометрии», т. е. разделу геометрии, изучающему связанные с целыми числами комбинаторные задачи, относящиеся к дискретным расположениям точек или геометрических фигур 1). Можно считать, что настоящая книга продолжает этот ряд книг по комбинаторной геометрии, поскольку рассматриваемая здесь задача является, по существу, комбинаторной проблемой о расположениях на плоскости конечных систем квадратов, удовлетворяющих некоторым наперед заданным условиям. Конечно, задачу, которой посвящена эта книга, вряд ли кто-либо сочтет особенно серьезной — это есть типичный вопрос из области «математических развлечений», какие охотно печатают журналы для семейного чтения в разделе «В субботний вечер». Однако вокруг на первый взгляд достаточно простого вопроса возникает так много любопытных соображений, относящихся к разным разделам математики и физики, вопрос этот с такой легкостью приводит к иным вопросам, явно безнадежно трудным (да и сама основная задача долго казалась неразрешимой даже таким серьезным ученым, как один из виднейших наших математиков первой половины этого века академик Н. Н. Лузин), первоначальная постановка вопроса так естественно обрастает разнообразными аналогами и вариантами, что мне захотелось побеседовать на столь, казалось бы, несолидную тему (см., впрочем, список литературы на стр. 109—111) с начинающими математиками. Мне кажется, что книга эта, рассчитанная на интересующихся математикой учащихся старших классов средней школы, на учителей математики и на будущих учителей — студентов математических отделений педагогических институтов или университетов, может дать некоторое представление о «математическом мышлении»: здесь мы имеем определенный «фрагмент математики», иллюстрирующий на одном примере некоторые достаточно характерные для математики ходы мысли, приемы, методы. Именно это обстоятельство явилось для автора книги решающим — здесь интересны, в первую очередь, не результаты, а приводящие к этим результатам рассуждения, заслуживает внимания не столько «что» (доказывается), сколько «как» (доказывается). И я хочу заранее подчеркнуть, что собранные в конце книги «нерешенные задачи» 1—X (точнее было бы сказать — задачи, решение которых неизвестно автору книги), большинство из которых являются, вероятно, достаточно трудными, не заслуживают, по моему мнению, того, чтобы тратить на них серьезные усилия: эти задачи приведены для иллюстрации сложности рассматриваемой здесь проблематики, а не как рекомендуемые темы самостоятельной научной работы. В противоположность этому включенные в основной текст книги задачи 1—20 (некоторые из которых, впрочем, тоже вовсе не просты) могут доставить читателю возможность полезной самопроверки; поэтому всякому, пожелавшему убедиться в полном овладении излагаемым в книге материалом, стоит попробовать решить эти задачи. При написании этой книги автор частично использовал составленный им некогда цикл задач для указанной на стр. 111 книги . Рукопись книги была внимательно прочитана В. Г. Болтянским, дружеская критика которого бесспорно способствовала улучшению текста. Много выиграла книга также от тщательной и компетентной работы ее редактора Ф. И. Кизнер. В процессе работы над книгой автор неоднократно советовался с А. М. Ягломом; при выполнении эскизов чертежей ему помогали М. С. Королева и Л. Н. Кузнецова

Автору приятно поблагодарить всех перечисленных лиц за помощь и внимание к его книге

Источник

Геометрические задачи (на разрезание)

Учебное занятие: Геометрические задачи (на разрезание)

развитие интереса к предмету

развитие творческих способностей учащихся

развития внимания, памяти, навыков самостоятельной и коллективной работы

развитие умственной самодеятельности, сообразительности и «смекалки»

Сегодня геометрические задачи (на разрезание) будут связаны с одной на вид простой геометрической фигурой.

Он давно знакомый мой,

Каждый угол в нем прямой.

Все четыре стороны

Вам его представить рад.

Главной заслугой квадрата стало использование его, как удобной единицы площади. Действительно, квадратами очень удобно замащивать плоские участки, а скажем, кругами такого не сделаешь без дыр и наложений. Часто математики вместо слов «нахождение площади» говорят «квадрирование».

Так, задача о нахождении площади круга называется задачей о квадратуре круга. Квадрат-главное действующее лицо в теореме Пифагора.

Квадрат на 20 равных треугольников

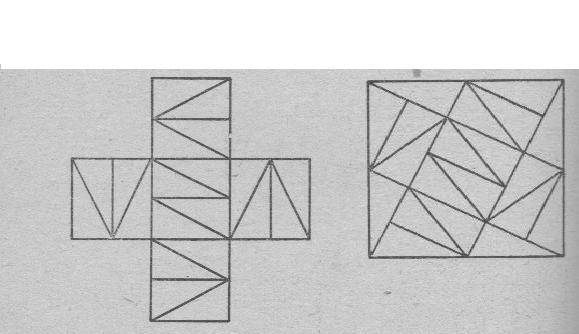
Разрезать квадратный кусок бумаги на 20 равных треугольников и сложить из них 5 равных квадратов.

Из креста – Квадрат

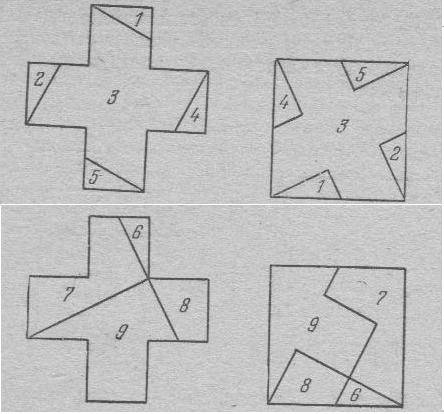
Крест, составленный из пяти квадратов, требуется разрезать на такие части, из которых можно было бы составить один квадрат.

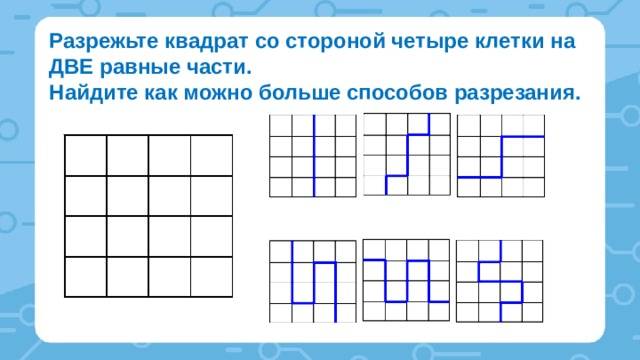
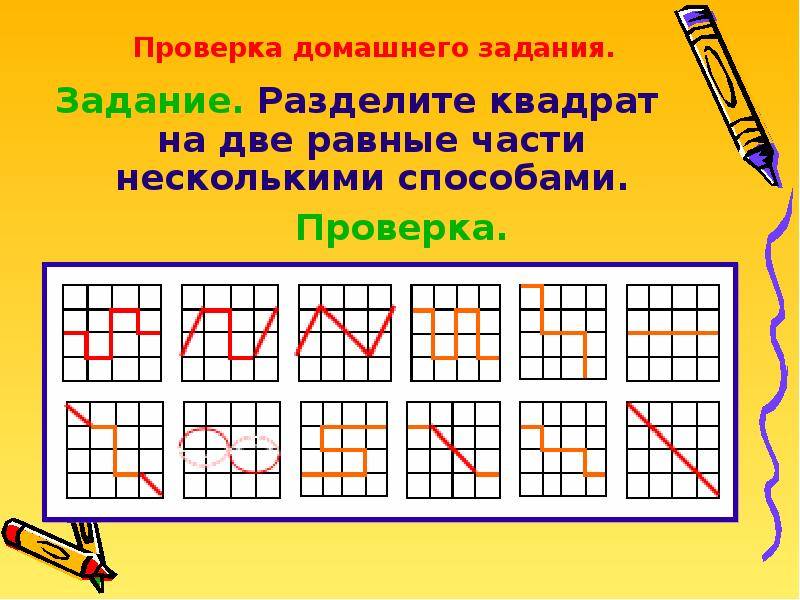
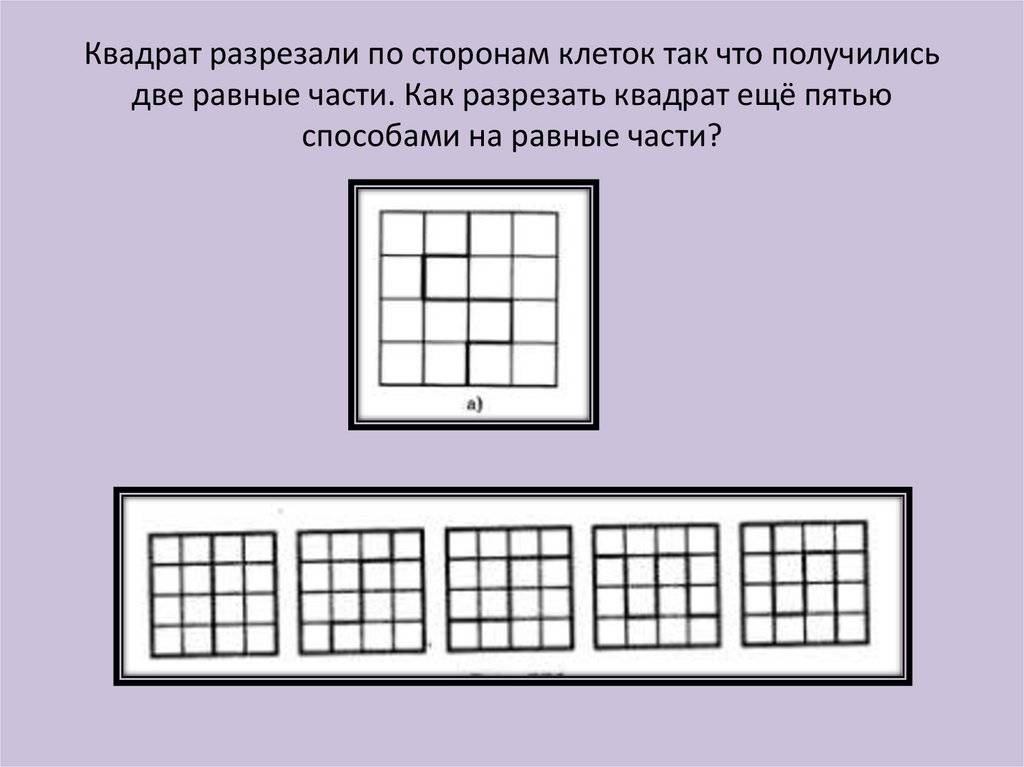
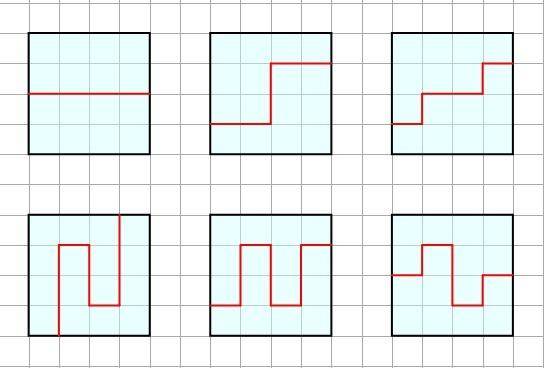
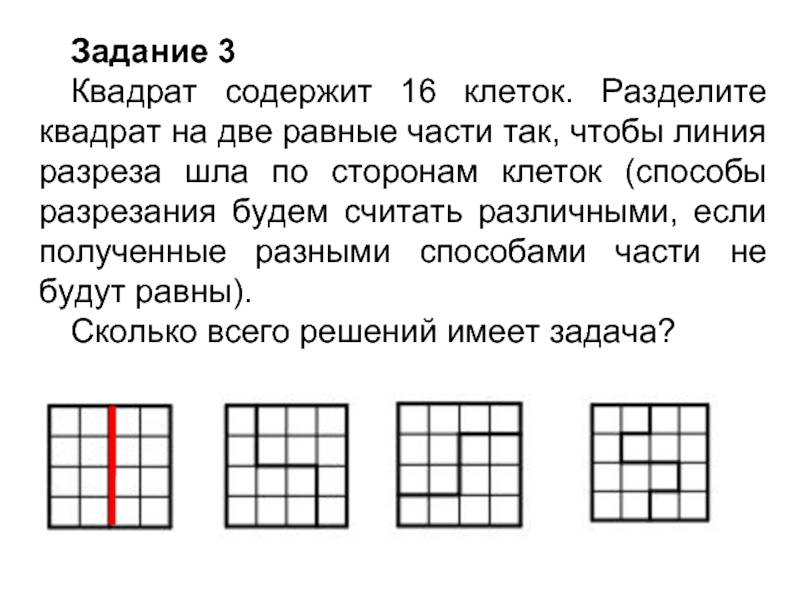
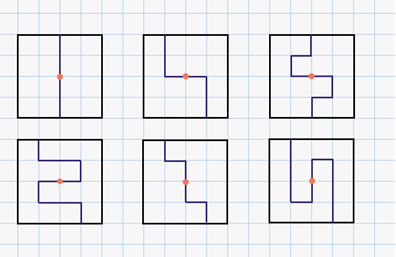
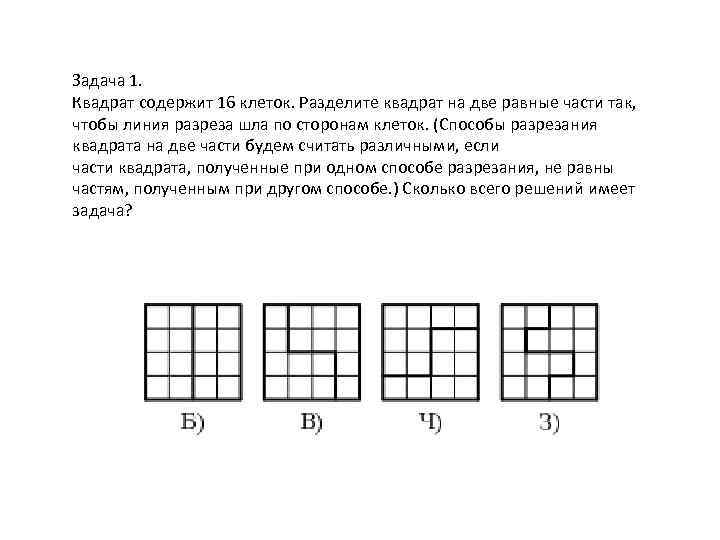
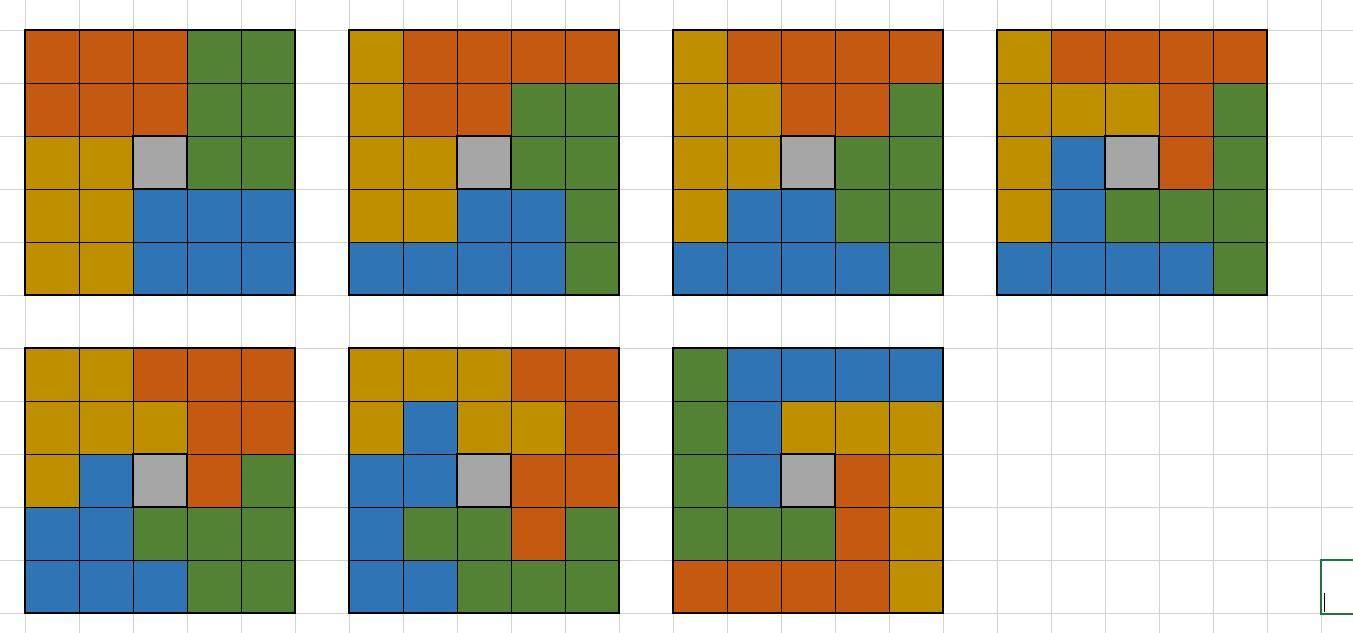
Квадрат содержит 16 клеток. Разделите квадрат на две равные части так, чтобы линия разреза шла по сторонам клеток.

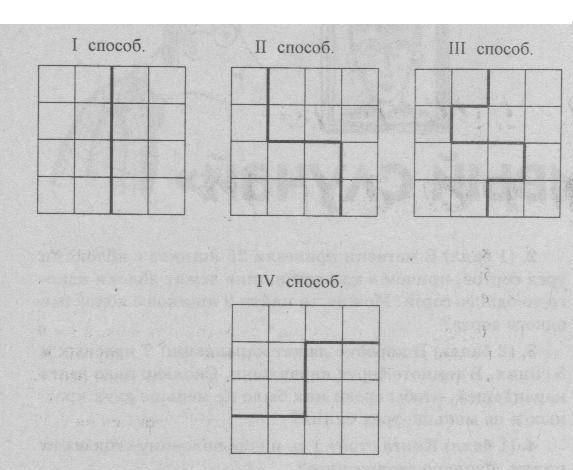
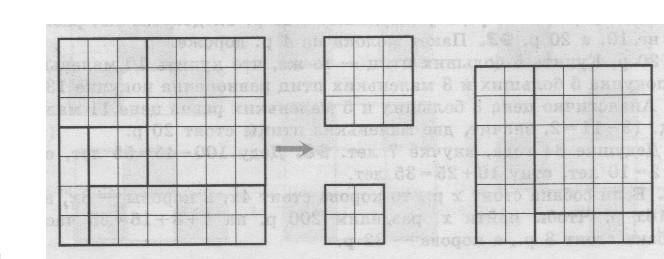
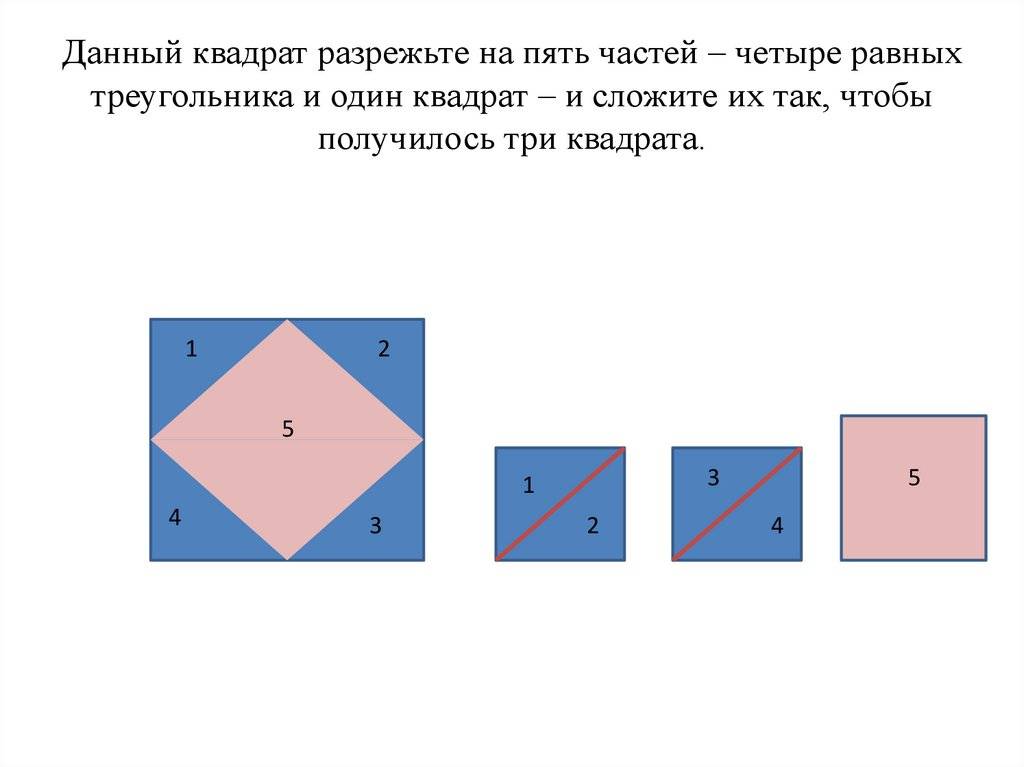
Разрежьте квадрат 7×7 на пять частей и переложите их так, чтобы получилось три квадрата: 2×2, 3×3 и 6×6.

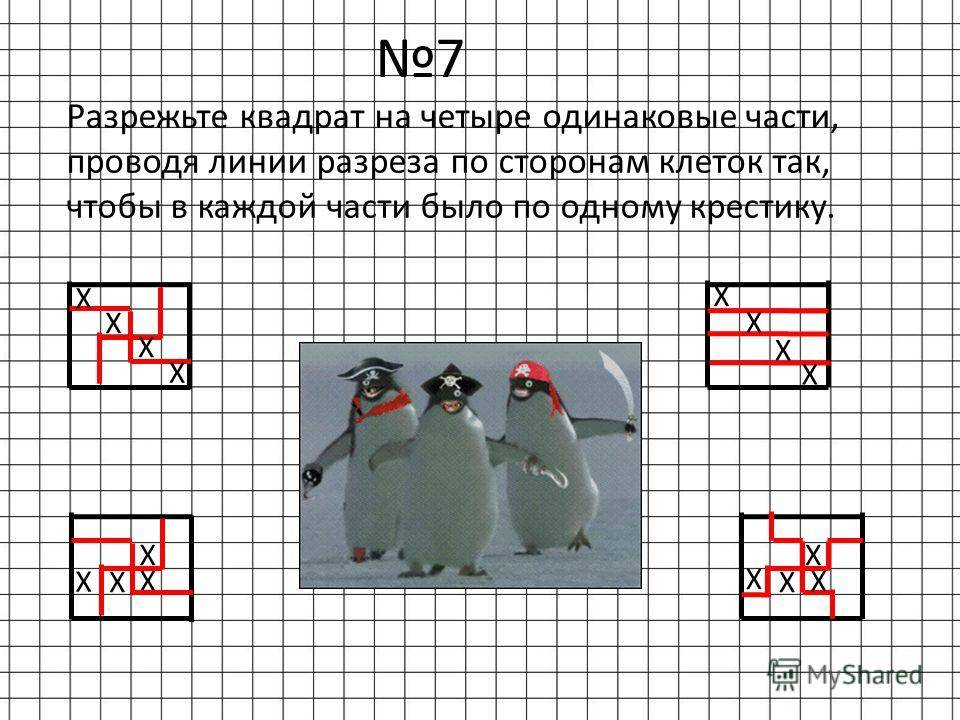
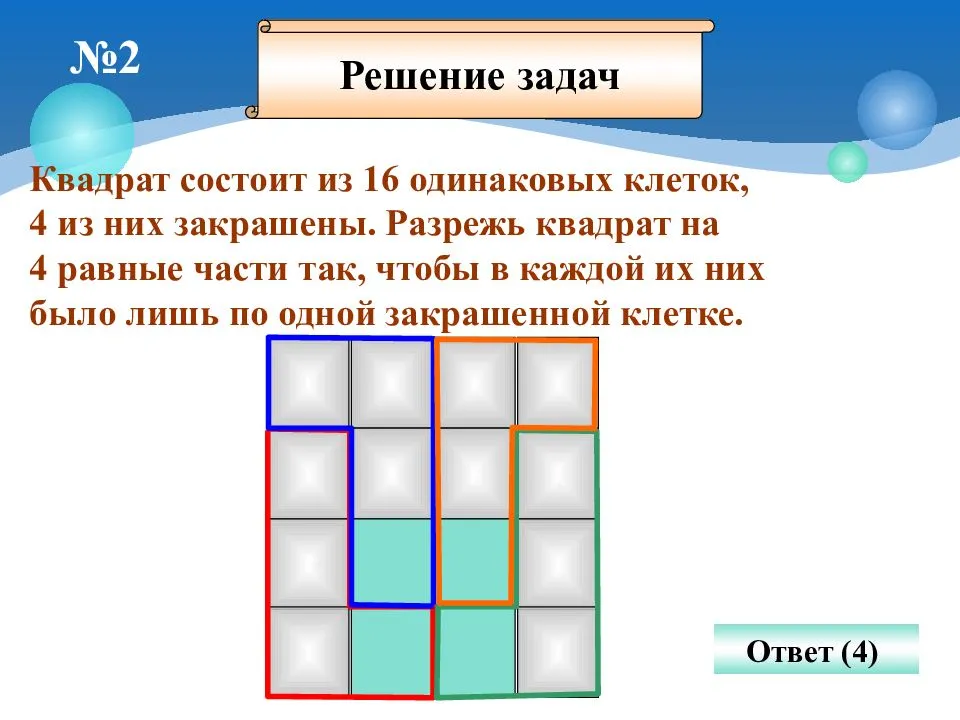
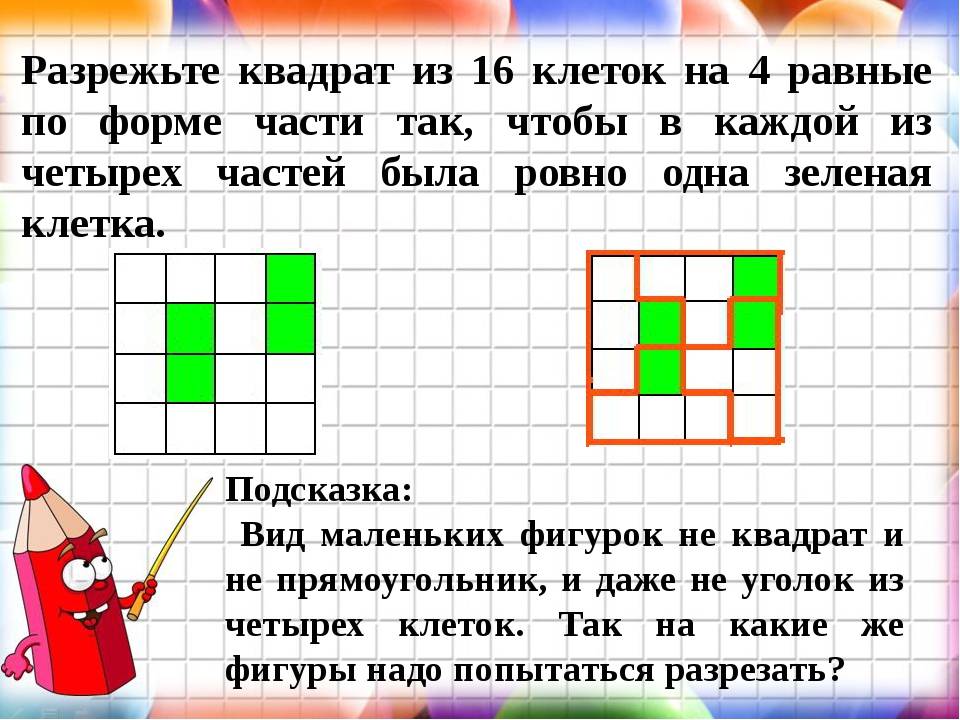
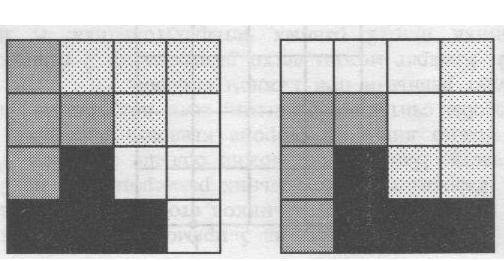
Разрежьте квадрат на 4 части одинаковой формы и размера так, чтобы в каждую часть попало ровно по одному заштрихованному квадрату.

Сколько всего квадратов на рисунке?

Разделить квадрат на более мелкие квадратики одинаковой площади очень просто: достаточно провести сетку равноотстоящих прямых, параллельных сторонам квадрата. Количество полученных квадратиков будет квадратом, да, да! Именно поэтому произведение двух одинаковых чисел назвали квадратом. А можно ли разрезать квадрат на несколько квадратиков, среди которых нет одинаковых?

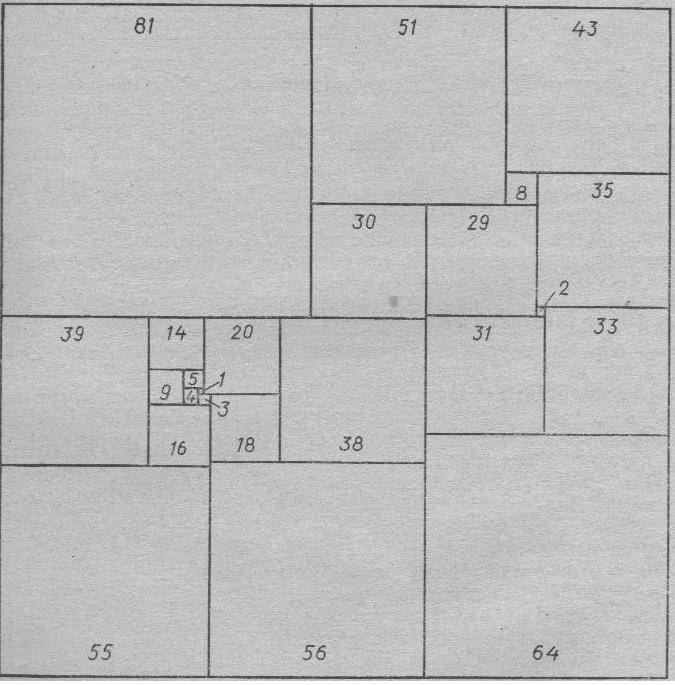
Этот вопрос долго оставался нерешенным. Многие даже выдающиеся математики считали, что такое разрезание невозможно. Но в 1939 году было построено разбиение квадрата на 55 различных квадратов. В 1940 году были найдены два способа разбиения квадрата на 28 различных квадратов, за тем-на 26 квадратов, а в 1948 году было получено разбиение на 24 различных квадрата. В 1978 году было найдено разбиение 21 различный квадрат и доказано, что разбиение на меньшее число различных квадратов найти уже нельзя.

И закончим сегодняшнее занятие занимательной игрой, связанной тоже с квадратом, «Танграм»

На рисунке показан квадрат, разделенный на 7 частей, из которых можно складывать разнообразные фигуры из альбома, предоставленным учителем.

Курс повышения квалификации

Сейчас обучается 801 человек из 76 регионов

Курс повышения квалификации

Сейчас обучается 283 человека из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 605 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-379194

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Попова предложила изменить школьную программу по биологии

Время чтения: 1 минута

Минпросвещения работает над единым подходом к профилактике девиантного поведения детей

Время чтения: 1 минута

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Занятие по ФЭМП в старшей группе ДОУ. Тема: Деление квадрата на две, четыре части

Демонстрационный материал: квадратный лист бумаги, ножницы, цифры; мяч.

Раздаточный материал: квадраты, ножницы, разрезные круги; тетради в клеточку, простые карандаши.

Ход занятия

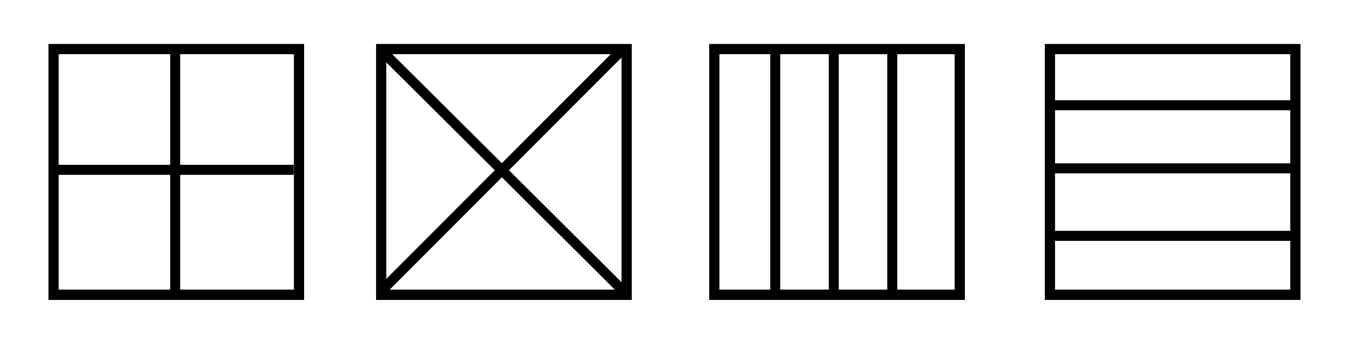
1. Деление квадрата на две, четыре части.

На фланелеграфе (или на доске) воспитатель помещает целый квадрат и две его части.

– Что это? (Квадрат.)

– А это что? (Показывает на две части.)

Ответы детей.

– Как вы думаете, можно ли из квадрата получить таких два прямоугольника?

– Если можно, то как?

– Правильно, разделить квадрат на две части.

Воспитатель показывает у доски, как сложить, разрезать 

– Сколько получилось частей? (Две.)

– А как мы их получили?

Воспитатель:

– А теперь давайте каждую часть разделим пополам.

Дети вместе с воспитателем делят каждую часть пополам.

– Сколько всего частей получилось?

– Покажите одну (две, три) части.

– Что больше (меньше): одна часть или две? (Три части или одна и т. п.)

– А если сложить две части, что получится?

– А если сложить четыре части?

– Как по-другому можно назвать две части? (Половина.)

– Сегодня мы научились делить квадрат на четыре равные части.

2. Гимнастика для глаз.

• Потереть ладонью о ладонь.

• Закрыть глаза и положить ладони на них.

• Поморгать, открыть глаза (ладони не убирать); поморгать, закрыть глаза.

• Потереть глаза кулачками, поморгать и открыть глаза.

3. Упражнение «Выполни правильно» (воспитатель показывает цифру два, а дети должны показать три части квадрата или одну часть, то есть на один больше или меньше).

Физкультминутка

Зайчикам не будет скучно,

Сделаем зарядку дружно?

Вправо, влево повернись,

Наклонись и поднимись.

Лапки кверху, лапки в бок

И на месте скок, скок, скок.

А теперь бежим вприпрыжку.

Молодцы, мои зайчишки!

Замедляем, детки, шаг,

Шаг на месте, стой!

Вот так.

4. Игра с мячом «Прямой и обратный счёт».

Дети стоят в кругу. Воспитатель бросает мяч ребенку и дает задание:

• Посчитай от 10 до 4; от 8 до 3 и т. д.

• Посчитай от 2 до 7; от 4 до 9 и т. д.

• Назови соседей числа 6 или 5 и т. д.

• Назови числа меньше 6 и т. д.

• Назови числа больше 3, но меньше 8 и т. д.

5. Игра «Собери фигуру» (разрезные фигуры).

6. Игра с пальчиками.

В понедельник – мандарин,

А во вторник – апельсин,

В среду – шоколад,

В четверг – мармелад,

В пятницу – виноград,

В субботу – печенье,

В воскресенье – варенье.

В понедельник я стирала,

Пол во вторник подметала.

В среду я пекла калач,

Весь четверг искала мяч,

Чашки в пятницу помыла,

А в субботу торт купила.

Всех подружек в воскресенье

Позвала на день рожденья.

7. Работа в тетрадях.

Разрежьте правильно на части

729. Как данный прямоугольник следует разрезать на две такие части, чтобы из них можно было сложить: 1) треугольник, 2) параллелограмм (отличный от прямоугольника), 3) трапецию?

730. Дан прямоугольник, основание которого в два раза больше высоты. 1) Как нужно разрезать данный прямоугольник на две части, чтобы из них можно было составить равнобедренный треугольник? 2) Как нужно разрезать данный прямоугольник на три части, из которых можно было бы составить квадрат?

731. Как можно равносторонний треугольник разрезать на: 1) два равных треугольника; 2) три равных треугольника; 3) четыре равных треугольника; 4) шесть равных треугольников; 5) восемь; 6) двенадцать?

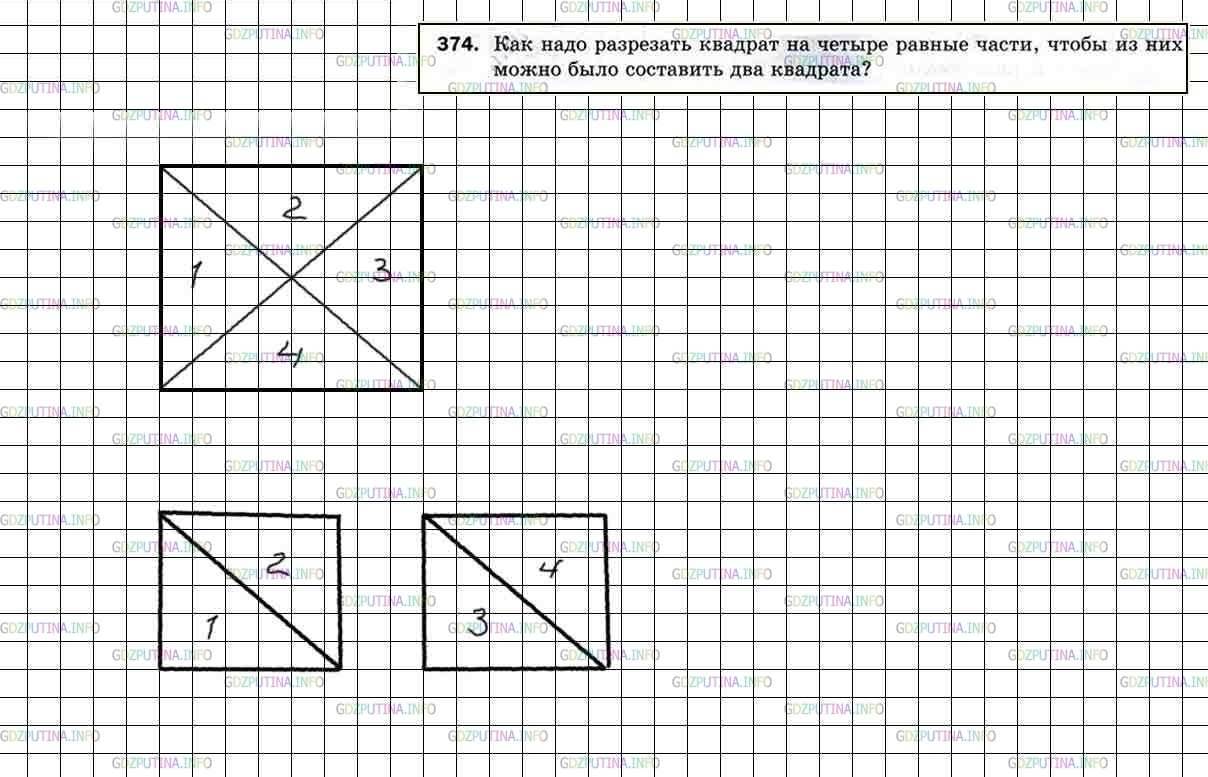
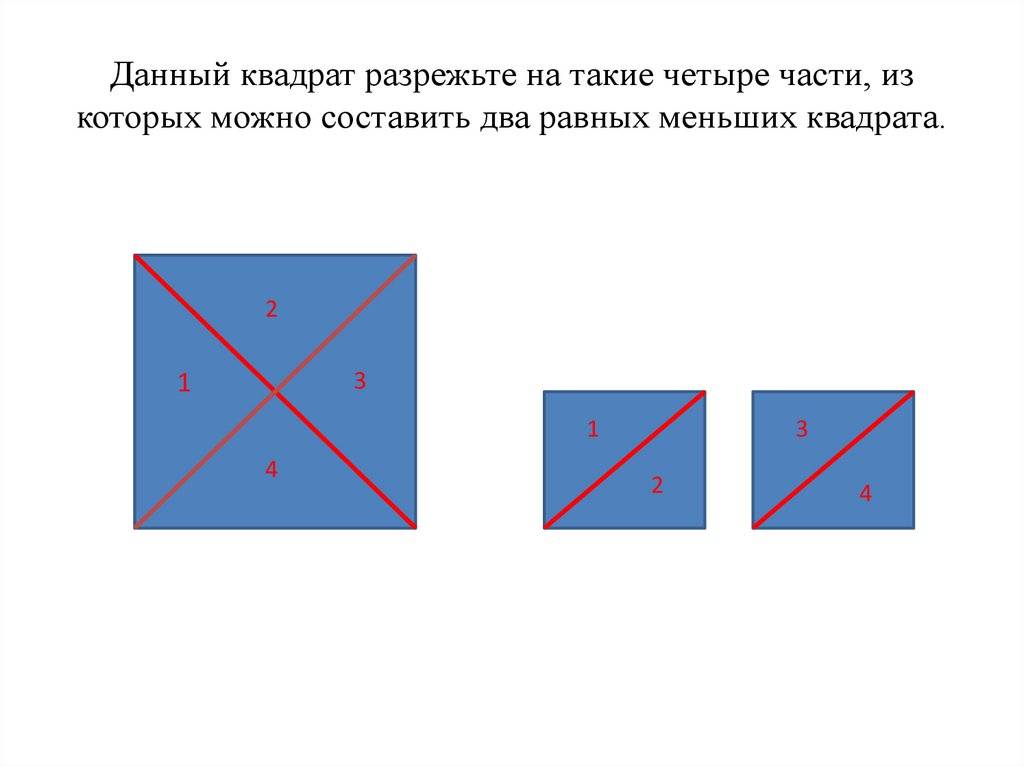
732. Даны два равных квадрата. Как разрезать каждый из них на две части так, чтобы из получившихся частей можно было сложить квадрат?

733. Как данный прямоугольник двумя прямолинейными разрезами разбить на два равных пятиугольника и два равных прямоугольных треугольника?

734. Даны два неравных квадрата. Как их следует разрезать на такие части, чтобы из них можно было сложить третий квадрат? Как выражается длина стороны третьего квадрата через длины сторон двух данных?

735. Прямоугольная плитка шоколада состоит из m*n единичных квадратных долек. Сколько разломов нужно сделать (одновременно ломается один кусок), чтобы разломить эту плитку на единичные квадратные дольки?

736. Сколько нужно сделать разрезов плоскостями так, чтобы из куба с ребром в 3 дм получить кубики с ребром в 1 дм?

737. Дан прямоугольный треугольник. Как следует разрезать его на две такие части, чтобы из них (не переворачивая обратной стороной) можно было сложить треугольник, симметричный данному относительно одного из его катетов?

738. Дан треугольник ABC. Как следует разрезать его на части так, чтобы из них (не переворачивая обратной стороной) можно было сложить треугольник, симметричный данному относительно основания АС?

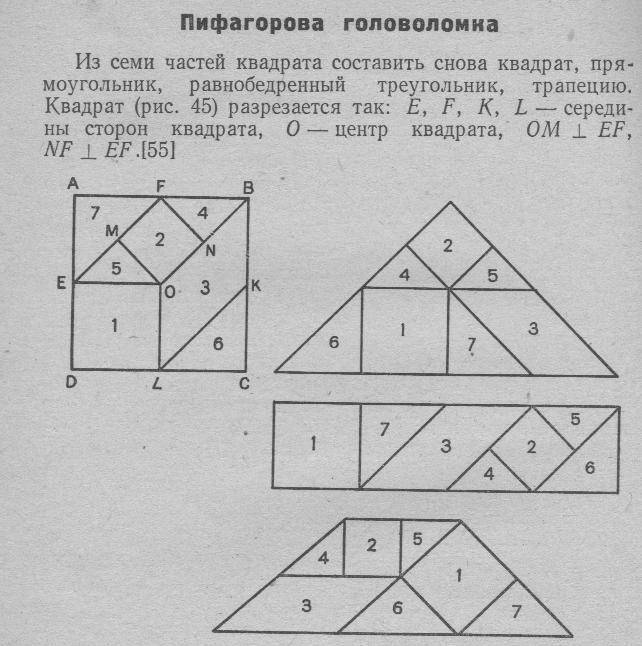
739. Разрежьте квадрат на части, как показано на рисунке 49, перемешайте их и затем сложите: 1) такой же квадрат; 2) прямоугольный равнобедренный треугольник; 3) прямоугольник, отличный от квадрата; 4) параллелограмм, отличный от прямоугольника; 5) трапецию.

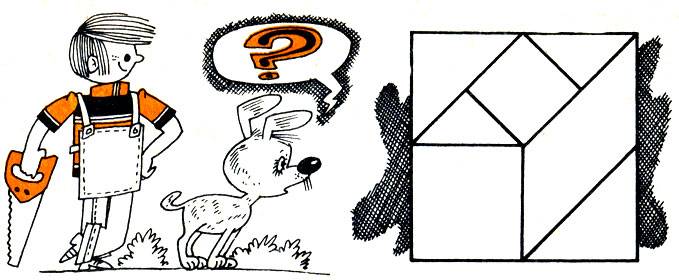Рис.49

740. Окрашенный куб с ребром в 10 см распилили на кубики с ромбом в 1 см. Сколько получится кубиков: 1) с одной окрашенной гранью; 2) с двумя; 3) с тремя; 4) совсем не имеющих окрашенных граней?

741. Как разрезать на две части прямоугольник со сторонами 16 и 9 см так, чтобы из них можно было сложить квадрат? (Разрез может быть в виде ломаной линии.)

742. Скопируйте каждую из фигур рисунка 50 и разрежьте ее на 4 равные части.

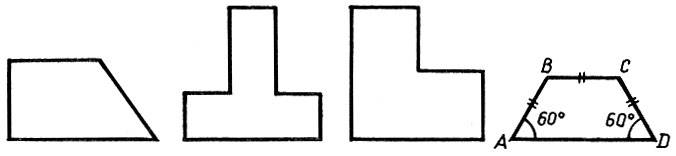Рис.50

743. 1) Как данный прямоугольный треугольник разрезать на остроугольные треугольники? 2) Как данный произвольный треугольник разрезать на остроугольные треугольники?

744. Внутри выпуклого стоугольника отмечены 10 точек, из которых никакие три не лежат на одной прямой. Многоугольник разрезается на треугольники так, что вершинами их служат все вершины данного стоугольника и все данные десять точек. Сколько получится треугольников?

Как резать высокий торт

Высокие торты и многоярусные конструкции требуют особых правил нарезания. Во-первых, высокие торты трудно нарезать на небольшие куски, они не будут держать форму. Во-вторых, в очень высоких тортах и тортах с многоярусными конструкциями спрятаны усилители (шпажки, подложки), поэтому разрезать торт нужно аккуратно.

Так, нарезать высокий одноярусный торт на большое количество кусков можно классическим способом. А затем каждую часть можно разрезать вдоль пополам. Так, если в торте содержится 6 коржей, то каждому гостю достанется полноценный кусок, состоящий из 3 слоёв бисквита.

Если такой торт нужно нарезать для фото, то в качестве куска лучше использовать сразу четверть торта. Так, кусок сможет ровно стоять на тарелке или лопатке. 

При нарезании каждого яруса многоярусного торта действуют те же правила, что и при нарезании обычного торта. Разрезая торт с 3 и более ярусами, верхний ярус снимают и начинают нарезать торт со средних ярусов. Только учитывайте, что внутри торта могут находиться острые шпажки. Не забудьте их достать и на всякий случай предупредите гостей.

Основные правила нарезки десертов

Создание красивого разреза начинается ещё задолго до нарезания торта, а именно на этапе его сборки. Чтобы разрез получился аккуратным, все коржи должны быть примерно одной толщины. 

Поэтому, если вы не уверены, что сможете ровно разрезать бисквит ножом, то перед нарезанием сделайте насечки по краям бисквита и ориентируйтесь по ним. С помощью кондитерской струны или нити также можно ровно нарезать бисквит.

А чтобы торт точно получился ровным, собирайте его в кольце или в форме, в которой выпекался бисквит. 

Стабильный крем и начинка

Крем и начинка также играют немаловажную роль в создании аккуратного разреза. При отсаживании крема ориентируйтесь на то, что его слой должен быть одинаковым и у краёв, и в середине, чтобы торт не выглядел горкой.  

Для этого используйте стабильный крем и отсаживайте его из кондитерского мешка по кругу либо, если крем не очень стабильный или вы используете мусс для начинки, собирайте торт в кольце. Только перед сборкой не забудьте проложить края формы ацетатной лентой.

Чтобы в каждом слое точно получилось одинаковое количество крема, воспользуйтесь весами и отсаживайте равные слои крема на каждый корж.

Стабильность начинки также очень важна. Если в торте предусмотрены ягодные или карамельные прослойки, не забывайте их уваривать до нужной консистенции либо используйте загустители (желатин, крахмал, пектин).

Время для стабилизации

Чтобы во время нарезания торта коржи не поехали и крем не вытек злосчастной лужей, не забывайте отводить нужное время на стабилизацию торта в холодильнике. Как правило, на этот процесс необходимо от 4 до 8 часов. 

Если торт муссовый и он заморожен, то размораживайте его правильно. Замороженные десерты должны размораживаться в холодильнике. Так, на них не выступит конденсат и их поверхность торта останется ровная и привлекательная.

Десерты следует нарезать сразу после того, как вы их достали из холодильника. Так, больше вероятность, что крем не размажется по коржам. А вот гостям лучше подавать уже разрезанный торт, который постоял минут 10-15 на столе и согрелся до комнатной температуры.

Острый нож

Острый хлебный нож – один из главных помощников кондитера. С его помощью можно аккуратно разрезать бисквиты и другие виды выпечки. Для нарезки торта также можно использовать такой нож. А можно воспользоваться более короткими острыми ножами.

Чтобы разрезать холодный торт, покрытый масляным или шоколадным кремом, и сохранить целостность покрытия, можно воспользоваться следующей хитростью: опустите нож в стакан с кипятком, подержите его в воде около минуты, затем насухо протрите салфеткой и сделайте разрез.

Использование салфетки

Каждый надрез нужно делать при помощи чистого, сухого ножа. Так, крем и бисквитные крошки, оставшиеся на ноже, не запачкают разрез. Для этого держите под рукой обычную бумажную салфетку. После каждого надреза начисто вытирайте нож.

Мастер-класс Оригами Делим квадрат на равные части Бумага

Деление квадрата на равные части — это всегда лишь подготовительный этап к складыванию. Однако без определенных навыков, как раз он и может оказаться достаточно сложным, особенно если количество частей, является простым числом:3, 5, 7, а так же 9. Об этом поподробнее.

Будем делить лист на три равные части.

Наметим середину верхней стороны. Для этого сделаем небольшую закрепку.

Сложим угол квадрата к середине противоположной стороны.

В таком случае, точка пересечения боковой стороны, противоположной этому углу и стороны, прилегающей к нему, делит сторону в отношении 1:2. Таким образом, с помощью только складок мы нашли треть стороны квадрата.

Расправляем квадрат. Закрепка на левой боковой стороне и есть 1/3 ее часть.

Используя полученную закрепку, формируем складку. При этом, она должна быть параллельна верхней и нижней сторонам.

Переворачиваем лист на противоположную сторону.

Складываем полученный прямоугольник пополам.

Таким образом, мы получаем три параллельных складки. Они разделили квадрат на три равные части.

Будем делить квадрат на пять равных частей.

Наметим с помощью закрепки середину боковой стороны.

Делаем сгиб, который проходит одновременно через нижний левый угол квадрата и нашу отметку. Правый нижний угол расположен по горизонтали на 2/5 от правого края.

Делим получившийся отрезок пополам. Ширина загнутой полоски и есть 1/5.

Расправляем лист. Теперь осталось разделить оставшуюся часть на четыре равные части.

Складываем левую боковую сторону к намеченной вертикальной складки. Таким образом, делим этот промежуток пополам.

Расправляем лист. Осталось каждую из широких полос разделить еще пополам.

Складываем левую боковую сторону к намеченной на предыдущем этапе складке.

Осталось, разделит последний сектор. Для этого, совмещаем правую боковую строну с крайней слева вертикальной складкой.

Расправляем лист. Деление на пять равных частей завершено.

Для того, что бы разделить лист на семь равных частей, необходимо предварительно разделить его на пять, как описано выше.

Делаем сгиб, при котором нижний правый угол совмещается со второй отметкой справа.

Расправляем лист. Точка на правой стороне, которая образовалась благодаря этому сгибу — это 3/7 от верхнего края или 4/7 от нижнего.

Совмещаем нижний правый угол с полученной на правой стороне точкой. Выполняем сгиб, который будет параллелен верхней и нижней стороне.

Складываем нижнюю сторону к полученной горизонтальной складке. Ширина этой полоски и будет 1/7 часть боковой стороны.

Делаем полученную выше складку «горой» и совмещаем ее с полученной выше отметкой, поделившей боковую сторону на 3/7 и 4/7.

Совмещаем верхнюю сторону с полученной на предыдущем этапе складкой.

Расправляем лист. Осталось поделить каждый из двух верхних прямоугольников еще пополам.

Совмещаем верхнюю сторону с полученной на предыдущем этапе складкой.

Совмещаем верхнюю сторону с самой нижней горизонтальной складкой.

Расправляем лист. Наш квадрат по горизонтали разделен на семь равных частей.

Для того, что бы разделить лист на девять равных частей, необходимо предварительно разделить его на три, как описано выше.

Делаем сгиб, при котором правый нижний угол совмещается с первой отметкой справа.

Точка, полученная на правой боковой стороне, будет делить ее на 4/9(сверху) и 5/9(снизу). Далее разделение на равные части может быть разным. Ниже один из способов завершить разделение квадрата на равные части.

Благодаря полученной точке на правой боковой стороне, делаем сгиб, параллельный верхнему и нижнему краю. Разница, на которую нижняя часть будет шире, чем верхняя — и есть 1/9.

Переворачиваем на противоположную сторону.

Отгибаем верхний слой бумаги. Сгиб должен совпадать с краем нижнего слоя.

Переворачиваем обратно на противоположную сторону. Разворачиваем лист.

Полученную складку на предыдущем этапе совмещаем с линией, которая получена с помощью закрепки.

Верхний край совмещаем с той же линией. Получилось что-то наподобие базовой формы «дверь». Теперь осталось каждый из четырех широких прямоугольников поделить еще на два.

Расправляем лист. Наш квадрат по горизонтали разделен на девять равных частей.

Источник