Эвольвентное зубчатое зацепление

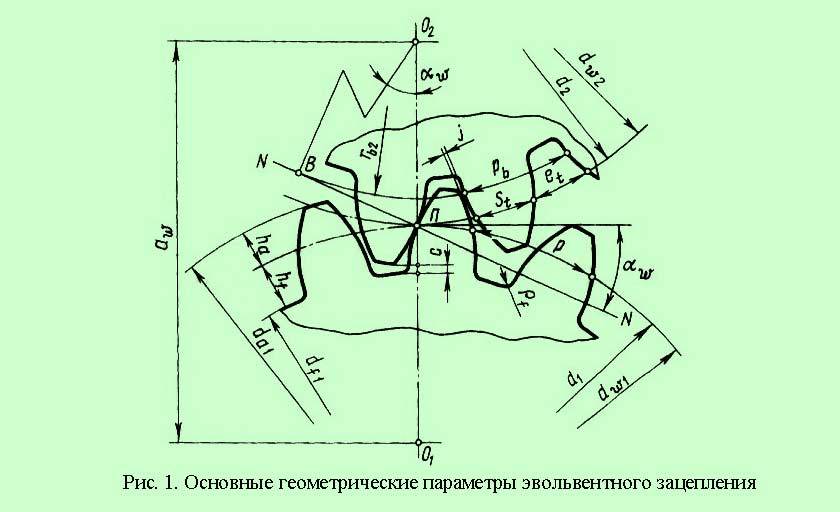
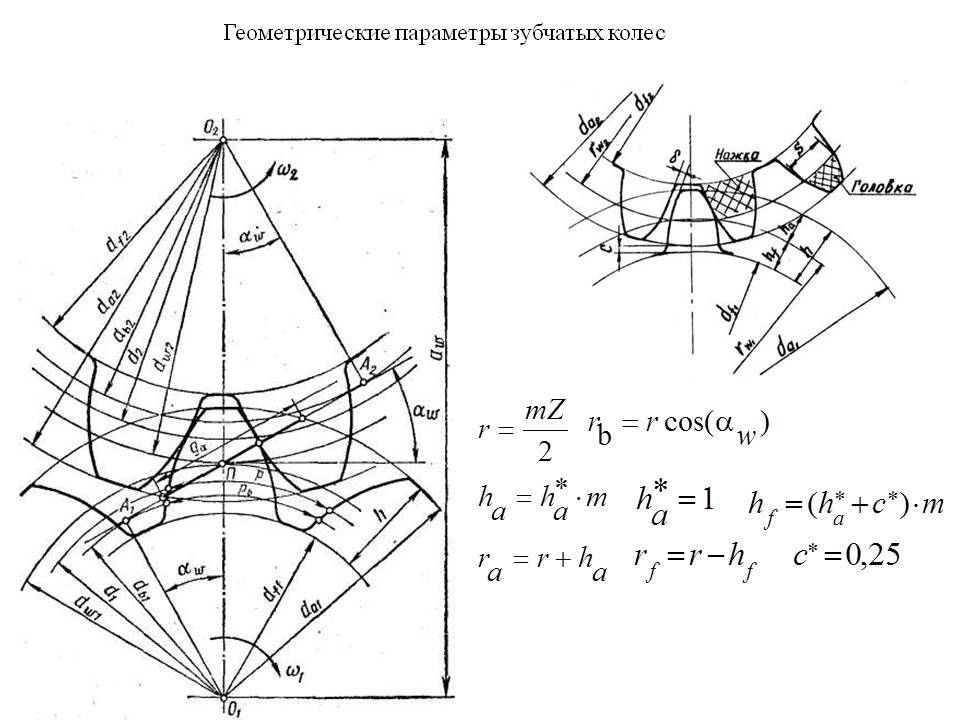
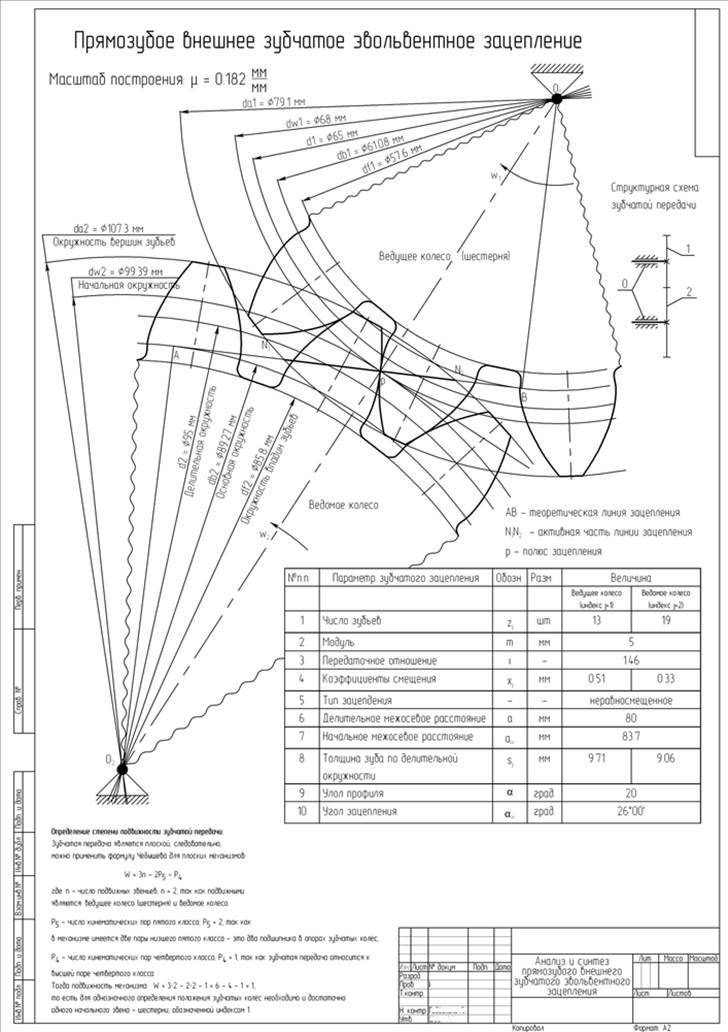
Исследование эвольвентного зацепления

Расчётно-пояснительная
записка к курсовому проекту по ТММ

Введение

Курсовой проект по теории машин и механизмов является первой
самостоятельной расчетно-графической работой в процессе обучения в университете.

Цель курсового проектирования – научить студентов самостоятельно решать
инженерные задачи, связанные с анализом и синтезом механизмов.

Данный проект состоит из графической части и расчетно-пояснительной
записки. Графическая часть проекта выполняется на трех листах формата А2.

Лист 1 (А2). Исследование эвольвентного зацепления (проектирование
зубчатой передачи из условия получения наименьших её габаритов и определение
некоторых характеристик этой передачи).

Лист 2(А2). Исследование шарнирно-рычажного механизма (кинематический и
динамический анализ конкретного плоского шарнирно-рычажного механизма).

Лист 3 (А2) Исследование шарнирно-ползунного механизма (изучение
кривошно-ползунного механизма, методов его исследования и регулирования
движения, определение момента инерции маховика машины).

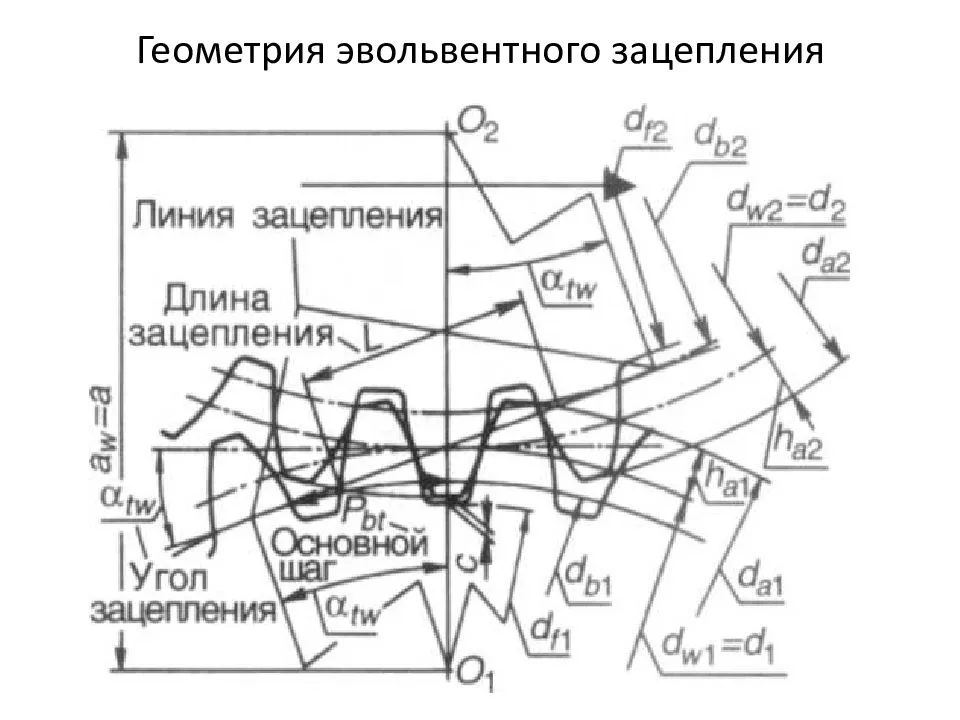
Исследование
эвольвентного зацепления

Исходные данные

Передаточное числ о U1/2 = Z2/Z1	Модуль зацепления m, мм	Масштаб	Скорость колеса 1, n1, об/мин	ε
2	5.5	5:1	1420	1,59

Определение скоростей и угловых скоростей звеньев механизма.

1. Известны длины звеньев механизма, величина и направление угловой скорости
ведущего звена, Расчет начинаем вести с ведущего звена механизма. Установив вид
движения звена, записываем соответствующую зависимость. В нашем случае кривошип
совершает вращательное движение.

Угловая скорость постоянна, поэтому скорость точки А определяется по
формуле:

где
. Из
точки О, которая называется полюсом плана скоростей, откладываем
перпендикулярно ОА отрезок оа, соответствующий скорости точки А.

.
Так как для решения задачи будем использовать графический метод, то вводим
масштаб скорости:

.
Для определения скорости точки В записывается векторное уравнение , связывающее
скорости точек А и В , используя теорему о сложении скоростей в переносном и
относительных движениях.

Здесь
и далее одной чертой подчеркнута скорость известная по направлению, и двумя
чертами – скорость, известная по величине и направлению.

Уравнение
имеет однозначное решение, если в нем два неизвестных. Поэтому на
предварительном этапе необходимо зафиксировать четыре параметра из шести. В
данном случае это удается сделать.

Строим
план скоростей. Из точки o проводим направление скорости V_B, а из точки а – направление V_BA.
Точка пересечения этих линий b определяет величины неизвестных скоростей:

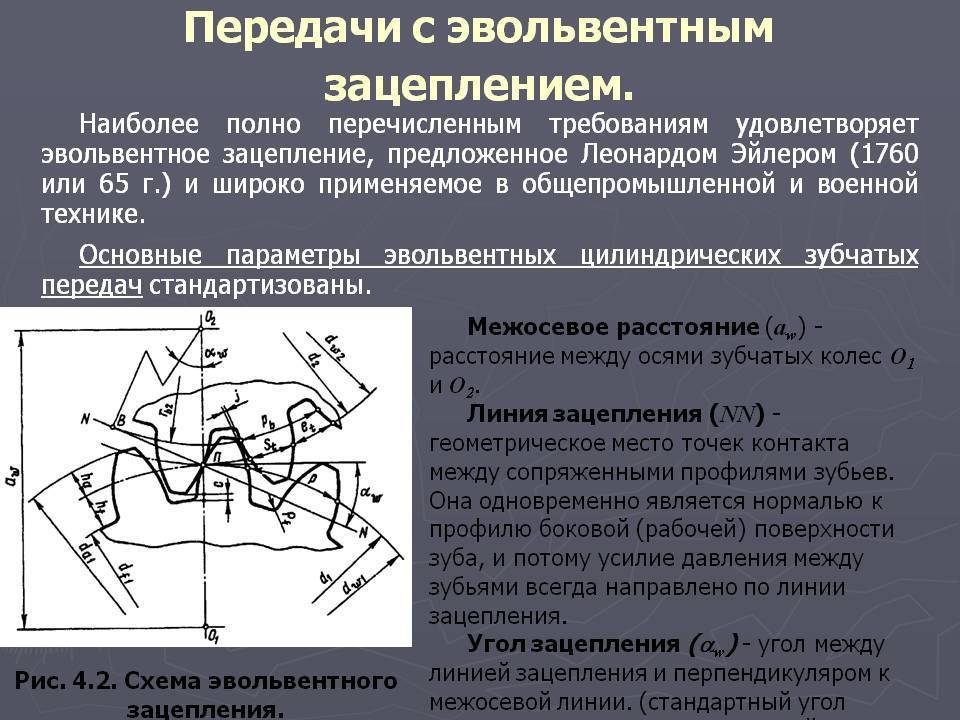
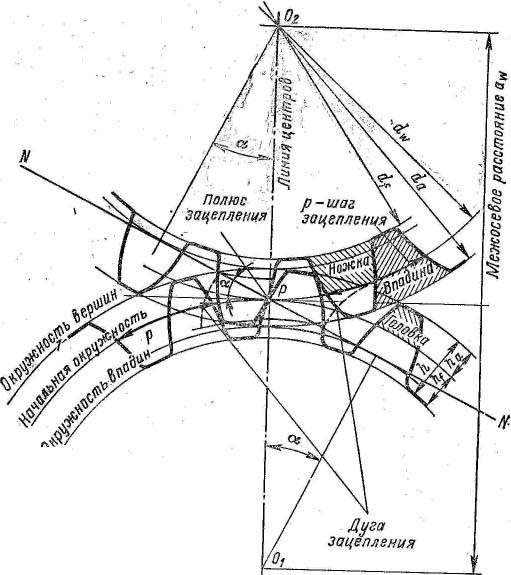
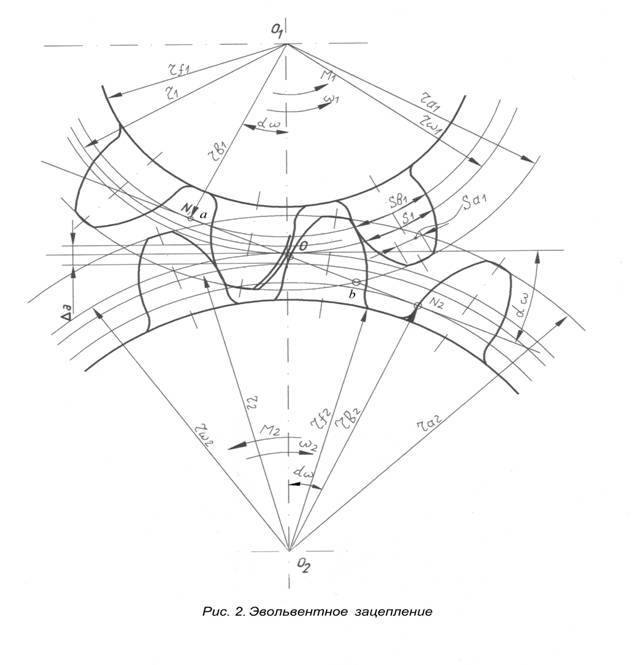
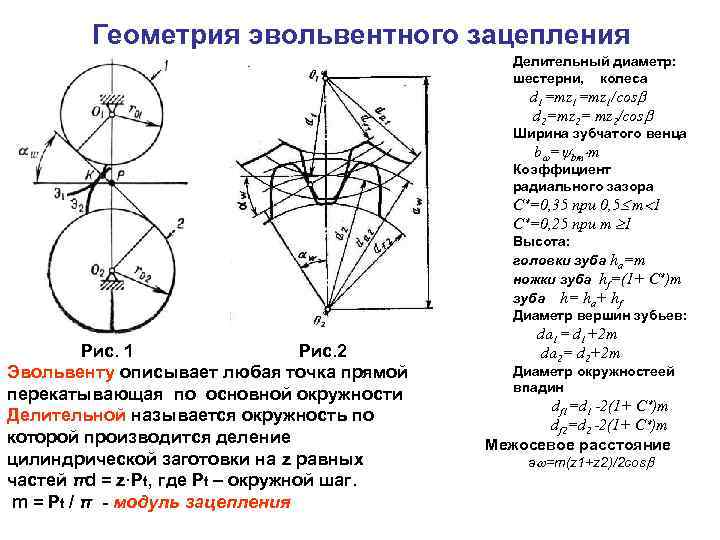
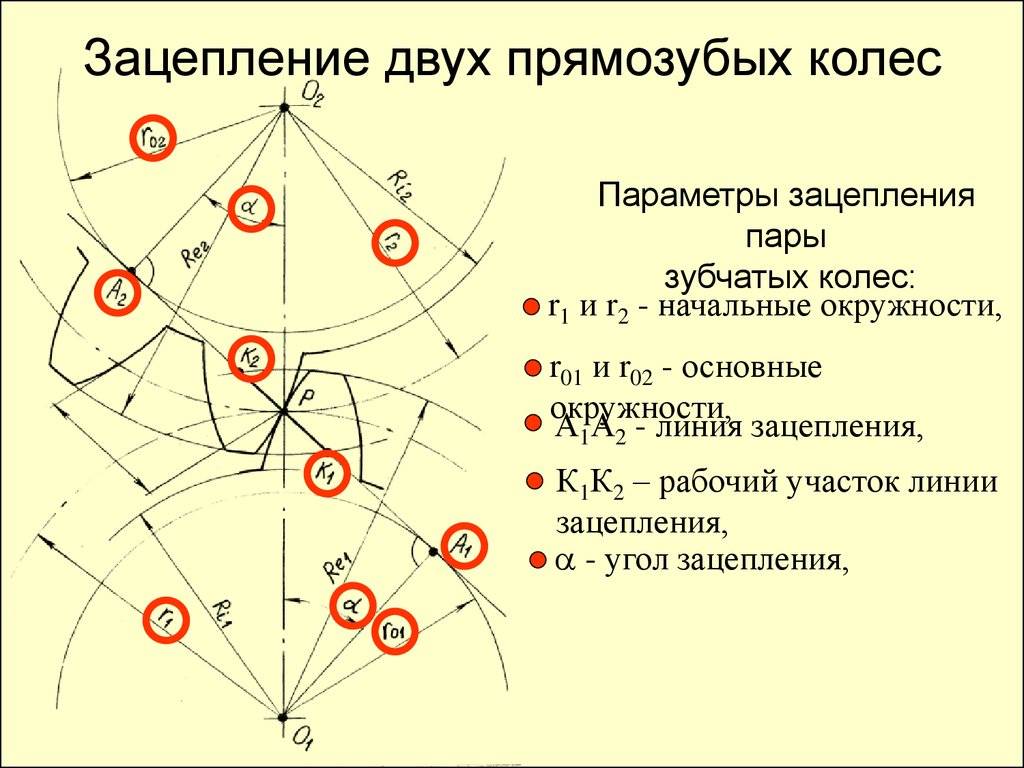
Эвольвентное зацепление

Эвольвентное зацепление — это зубчатая передача, которая нечувст­вительна к изменению межосевого расстоя­ния. Его изготавливают методом обкатки.

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут из­готавливаться на одном оборудовании, не­зависимо от количества зубьев и размеров головки.

Модули зацепления цилиндрических и ко­нических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных пе­редач по DIN 780; модули шлицевых соедине­ний по DIN 5480; модули зубчатого зацепле­ния нормального профиля для шестерен со спиральными зубьями по DIN 780.

Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; чер­вячных передач — DIN 3975; шлицевых соеди­нений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).

Форма зубьев гипоидных передач регла­ментируется стандартом DIN 867. В допол­нение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы заце­пления 12°, 14°30\ 15°, 17°30′_| 22°30′ и 25°.

Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)

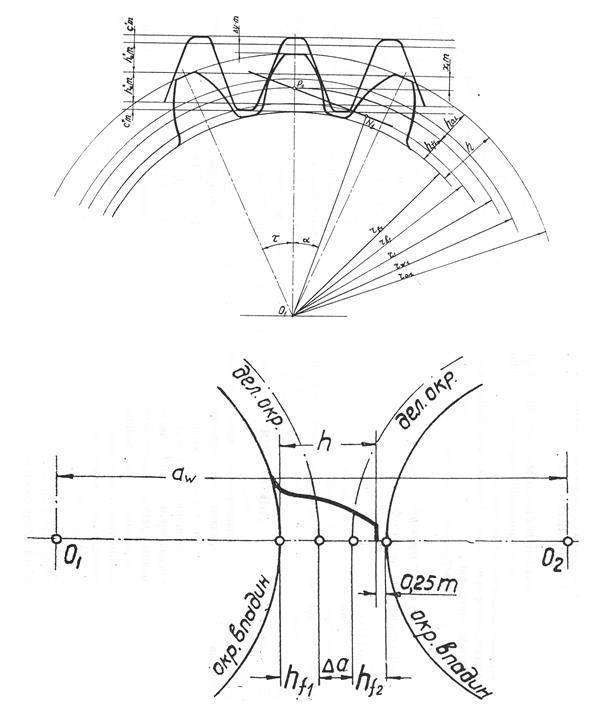
Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (из­менение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подреза­ния у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.

Зубчатые передачи с точно заданным межосевым расстоянием

У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса произво­дится на одинаковую величину, но в противо­положных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.

Зубчатые передачи с изменяемым межосевым расстоянием

Изменение высоты головки зуба для ше­стерни и зубчатого колеса производится независимо друг от друга, поэтому межосе­вое расстояние передачи может изменяться. Допускаемые отклонения линейных разме­ров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.

Подставляя j_η = 0 в приведенные ниже формулы, рассчитывают параметры за­цепления без зазора между зубьями. Для определения зазора между зубьями допу­скаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в за­висимости от требуемой степени точности зубчатой передачи. Следует отметить, что не обязательно стремиться к нулевому за­зору между зубьями. Для компенсации имею­щихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес. Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.

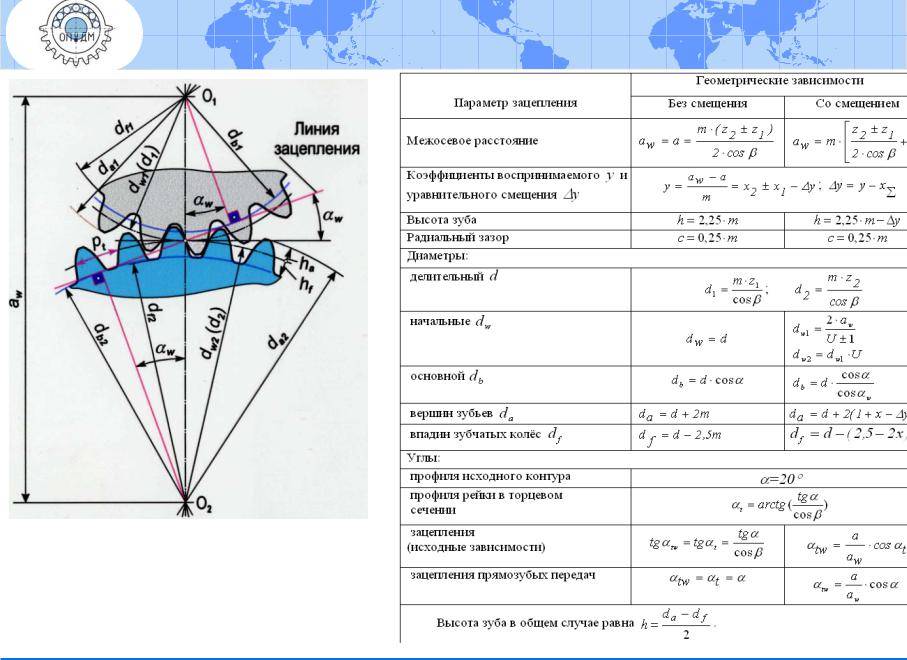
В таблице ниже приведены формулы для расчета зубчатой передачи:

Цилиндрические зубчатые колеса(шестерни):

Цилиндрические зубчатые колеса используются в передачах, где оси валов располагаются параллельно относительно друг друга. При этом они могут располагаться как горизонтально, так и вертикально.

В зависимости от формы продольной линии зуба зубчатые колеса бывают: прямозубые, косозубые и шевронные.

Рис. 1. Цилиндрические зубчатые колеса: прямозубые, косозубые и шевронные

Прямозубое колесо. Этот вид шестерен ввиду своей простой конструкции является наиболее внедряемым в различных системах. В таком виде зубья шестерен располагаются в плоскости, которая перпендикулярна оси вращения. В отличии от косозубых и шевронных колес у данного вида предельный крутящий момент ниже.

Косозубое колесо. Зубья для данного вида колес выполняются под определенным углом к оси вращения шестерен, а по форме образуют часть винтовой линии. По сравнению с прямозубым колесом при работе зубьев данного вида зацепление зубьев происходит плавнее, а за счет увеличенной площади контакта предельный крутящий момент выше. Но для работы колес с косым зубом приходится применять упорные подшипники, так как возникает механическая сила, направленная вдоль оси. В основном косозубые колёса используются там, где нужны передачи большого крутящего момента на высоких скоростях.

Шевронное колесо. Этот вид имеет зубья, которые выполнены в форме буквы V на плоскости вращения колеса. Главной особенностью шевронных колес является то, что силы на осях обеих половин компенсируются, вследствие чего отпадает необходимость в использовании упорных подшипников. Различают шевронное и многошевронное цилиндрическое зубчатое колесо, состоящее соответственно из двух и более полушевронов, а также шевронное цилиндрическое зубчатое колесо со сплошным венцом и разделенными полушевронами.

В отдельные виды выделяются: цилиндрическое колесо с круговыми зубьями, цилиндрическое колесо со смещением (без смещения), циклоидальное, эвольвентное и цевочное цилиндрическое колеса.

Колесо с круговыми зубьями. Передачу с такими колесами называют передачей Новикова. При такой передаче контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс. Зубья данного вида колеса выполнены в виде полукруга, радиус которого подбирается под нужные требования. Колеса с круговыми зубьями в сравнении с косозубыми обладают более высокой нагрузочной способностью зацепления, высокой плавностью и бесшумностью работы, но при тех же условиях работы у них снижен КПД и ресурс работы, что не позволяет их применять широко.

Колесо со смещением либо без смещения. Это зубчатое колесо, зубья которого образованы при номинальном положении исходной производящей рейки, характеризуемом отсутствием касания (касанием) делительных поверхностей исходной производящей рейки и обрабатываемого зубчатого колеса.

Циклоидальное колесо. В данном виде профили зубьев шестерни выполнены по циклоидальной кривой. Однако при таком способе зацепления шестерен имеется большой недобор чувствительности из-за изменения расстояния между осями. Циклоидальное колесо применяется в основном в приборостроении. Колесо сложно в изготовлении, поскольку при его создании требуется использование очень многих специальных зуборезных инструментов.

Цевочное колесо. В данном случае зубья одного из колес имеют вид пальцев в форме цилиндра. Такой вид шестерен образовался на базе циклоидального колеса и получил более широкое применение как в машиностроении, так и в приборостроении.

Определение основных элементов зубьев и их зацепления.

Определив минимальное число зубьев первого и второго колеса, приступаем к
определению основных элементов зубьев, участвующих в зацеплении:

1.      Определим
высоту головки  и ножки зуба:

h_a=4,4 мм

2.      Вычисляем диаметры начальных окружностей 1-ого и 2-ого колеса:

мм

мм

3.      Вычисляем диаметры окружностей вершин зубьев 1-ого и 2-ого
колеса:

мм

 мм

4.      Определяем окружности впадин зубьев 1-ого и 2-ого колеса:

мм

мм

5.      Определяем шаг зацепления:

мм

6.      Определяем толщину зуба:

мм

7.      Определяем ширину впадины:

мм

8.      Определяем межосевое расстояние:

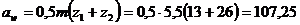мм

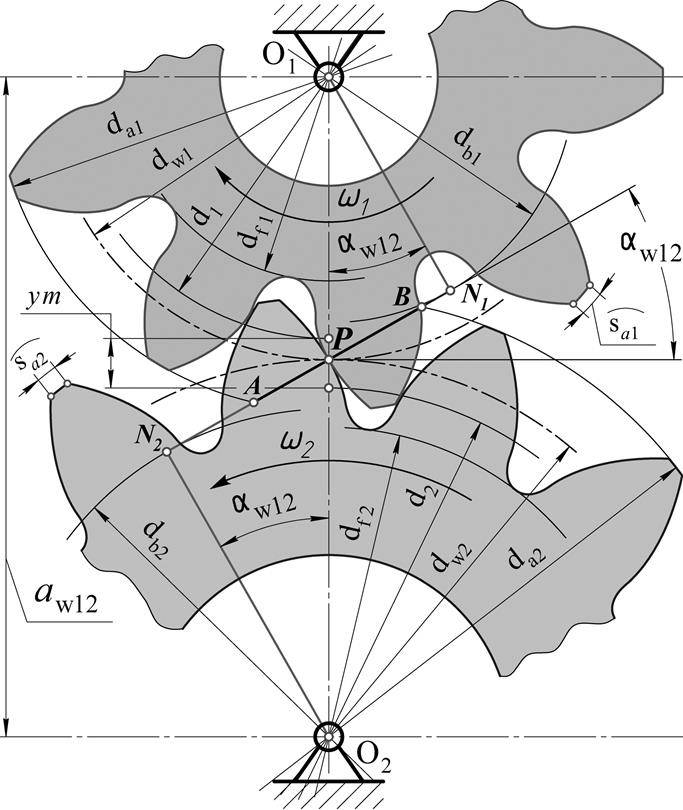
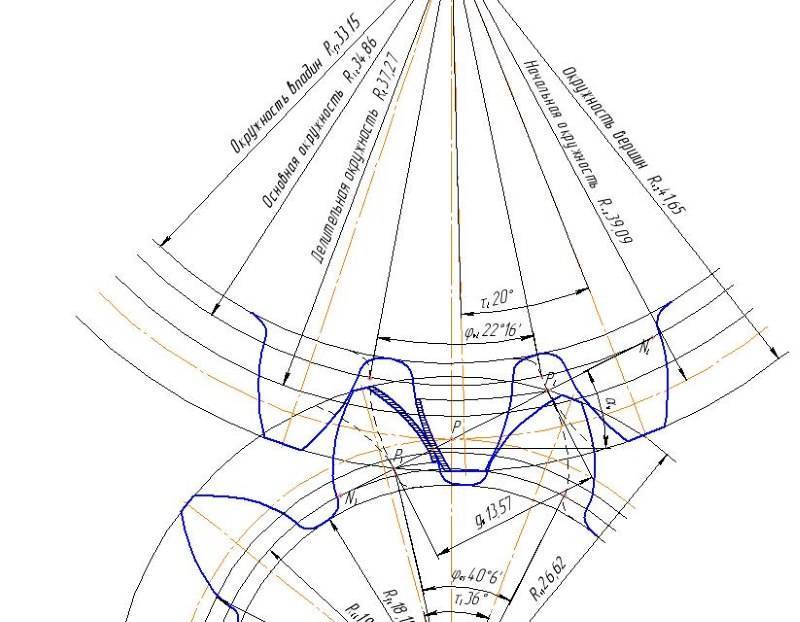
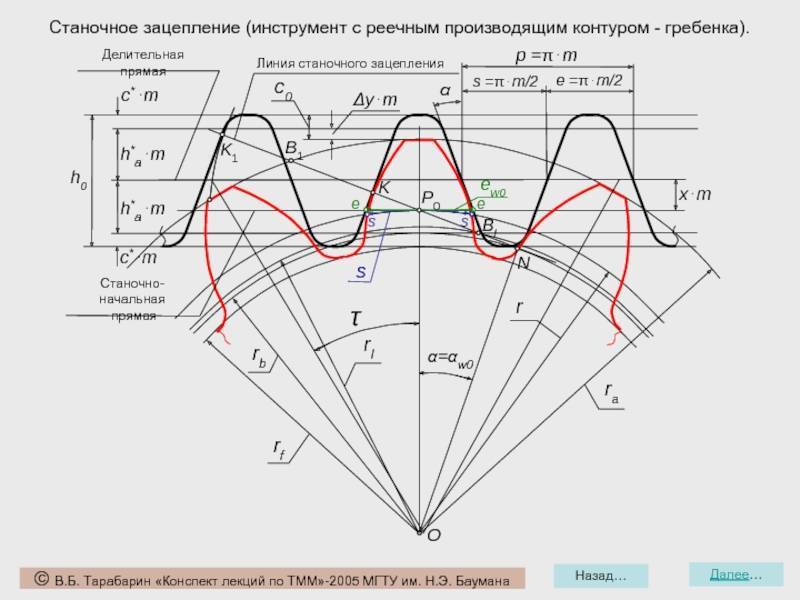
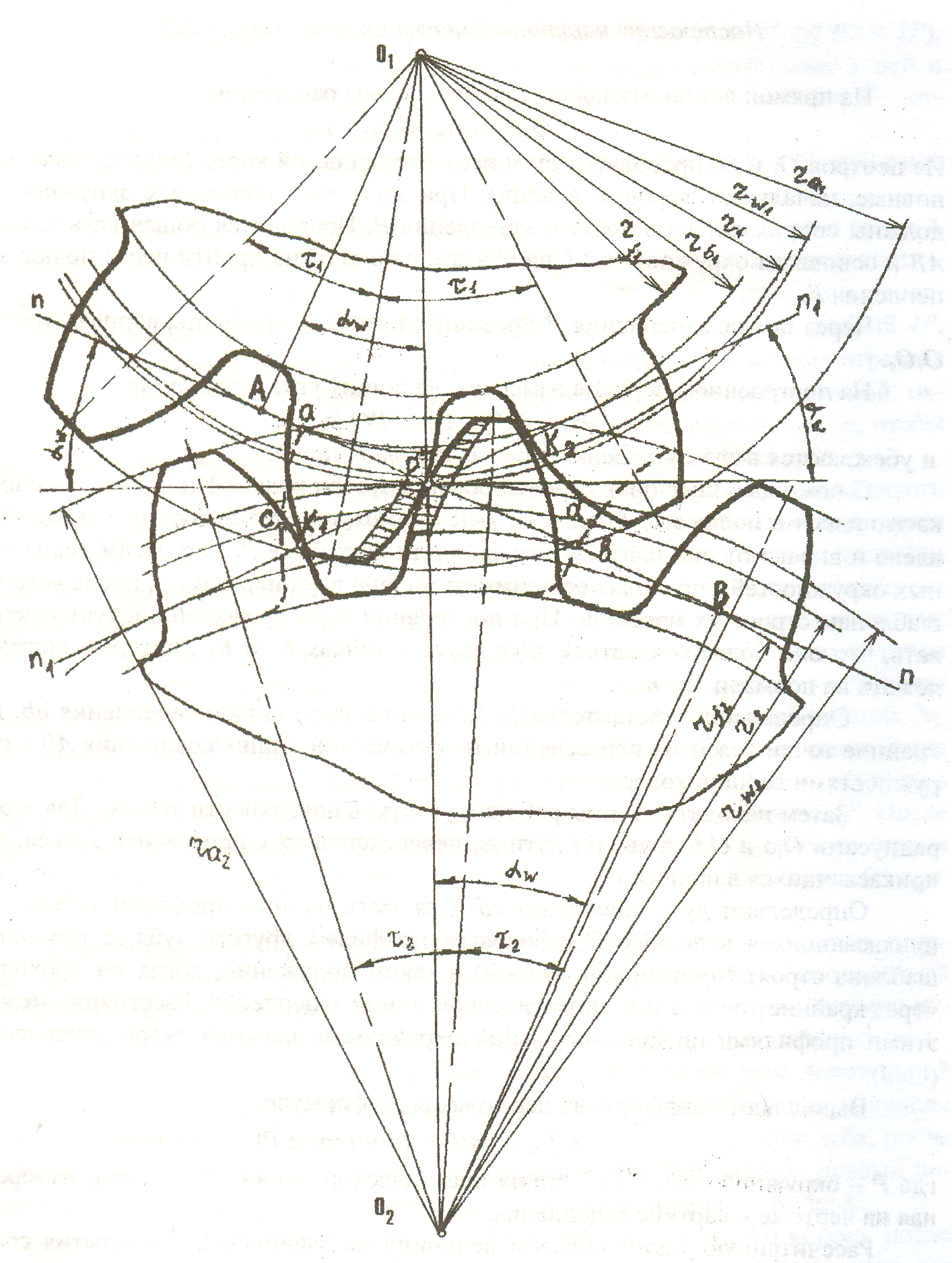
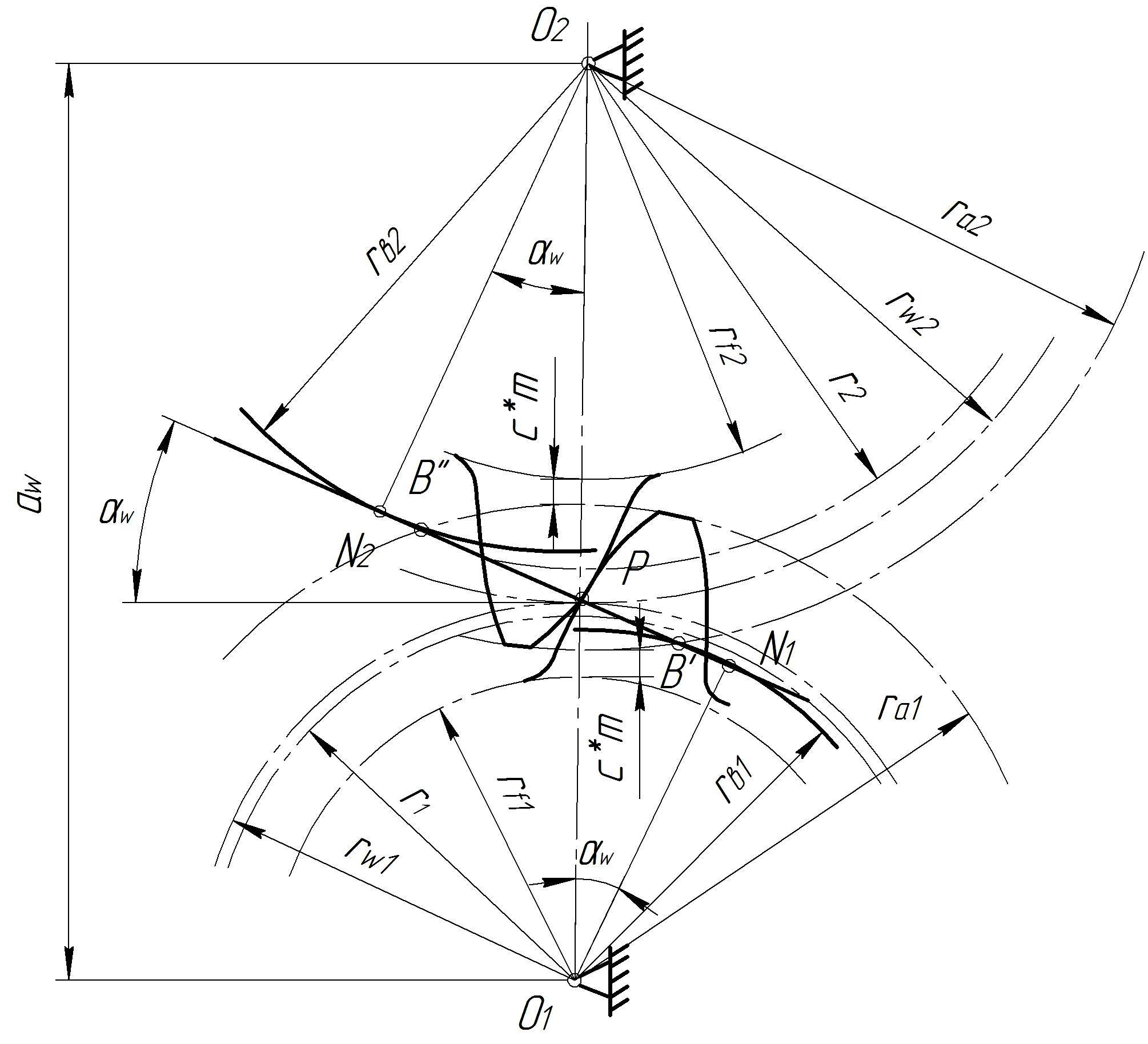
Выполнив пункты 1-8, приступаем к построению картины эвольвентного
зацепления и определения основных её элементов:

а.
Фиксируем на ватмане межцентровое расстояние O₁O₂. Проводим начальные окружности, окружности выступов и
впадин 1-ого и 2-ого колеса. Начальные окружности касаются друг друга в полюсе
зацепления Р, который находится на прямой O₁O₂. Через точку Р проводим перпендикуляр PE, а
также линию зацепления LM, под углом  к прямой
PE.

б.
Зафиксировав линию пересечения LM из точек O₁ и O₂ опускаем
перпендикуляры на линию зацепления LM, и через точки N₁ и N₂ проводим
основные окружности радиуса O₁ N₁ и O₂N₂.

в.
Приступаем к построению профиля зуба 1-ого колеса. Для этого разбиваем основную
окружность возле точки N₁ на дуги
с хордами 20 мм. И проводим через полученные точки касательные к основной
окружности, фиксируем на линии зацепления отрезок PK, длинной 30
мм., считая точку К точкой касания зубьев колес. Ставим острие циркуля в точку N₁и проводим дугу K₁K₁ радиуса N₁K₁ до середины соседних областей с точкой К
(приблизительно). Оставив карандаш в точке K₁, перебросив острие в n₂, изменив раствор циркуля, проводим дугу K₁K₂
до середины соседней области
(приблизительно) радиусом n₂K₂. Оставив
карандаш в точке K₂,
перебрасываем острие циркуля в точку n₃ и проводим дугу K₂K₃ до середины соседней области радиусом n₃K₃
и т.д. пока не достигнем основной
окружности.

г.
Одна сторона профиля зуба по эвольвенте вычерчивается от окружности вершин
зубьев колеса до основной окружности, от основной окружности до окружности
впадин, профиль зуба вычерчивается по радиусу с закруглением у окружности
впадин радиусом 0.2m:

Тогда
с учетом масштаба:

Для
построения полного профиля зуба откладываем по начальной окружности толщину
зуба S_t, используя понятие центрального угла.

Отложив
ширину впадины по начальной окружности, применяя понятие центрального угла,
наносим еще 3 профиля зуба. Затем строим профиль зуба 2-ого колеса, где К –
точка касания зубьев, отправной считаем точку N₂

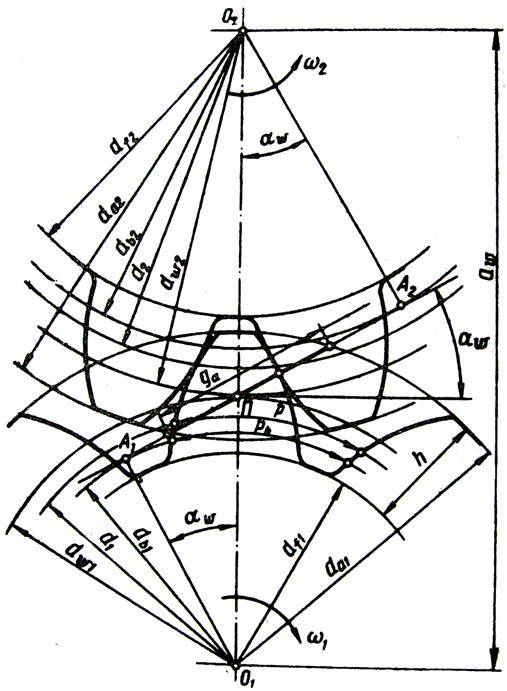
Построив
картину эвольвентного зацепления определяем коэффициент перекрытия по формуле:

где
B₁B₂ – длина
зацепления, измеряемая по чертежу (где B₁ – точка входа зубьев колес в зацепление, т.е. точка
пересечения линии зацепления LM и окружности вершин 2-ого колеса; B₂ – точка выхода колес из зацепления, т.е. точка
пересечения линии зацепления и окружности вершин 1-ого колеса).

При расчете учтем масштаб чертежа:

Теоретическое
значение . При 1.27 условие зацепления соблюдается.

После
фиксации B₁B₂ показываем
штриховкой активные профили зубьев колес, т.е. те участки зубьев, которые
участвуют в зацеплении. Активный профиль 1-ого колеса ограничен окружностью
вершин этого колеса и окружностью O₁B₁ (окружности показаны пунктиром).

.
Строим график относительной скорости скольжения зубьев, для этого выносим B₁B₂
с фиксацией P и K.

Вычисляем
для точки К скорость скольжения зубьев( точка К – точка касания зубьев,
располагается внутри отрезка B₁B₂):

механизм шарнирный рычажный кривошипный

Найденную
скорость точки К изображаем отрезком 10мм. и определяем масштаб скорости:

м/с

Из
двух значении выбираем наибольшее:

Таким
образом, наибольшая скорость скольжения зубьев характерна для точки B₁
в момент начала зацепления.

Исследование
шарнирно-рычажного механизма

Длины звеньев механизма: L_OA = 0,25 м, L_AB = 0,75 м, L_AС
= 1 м, L_АS2 = 0, 5 м, L_СS4 = 0,4 м, X₁ = 1,4 м. ????₁ = 30 c-1, oa =70мм. Масштаб чертежа: K_L = 0,005 м/мм. m₂ = 40 кг, J₂ = 4,4 кг м2,
m₃ = 20 кг, J₃ = 0,8 кг м2,
m = 60 кг

Определить скорости и ускорения точек механизма, угловые скорости и
ускорения, а также усилия в кинематических парах.

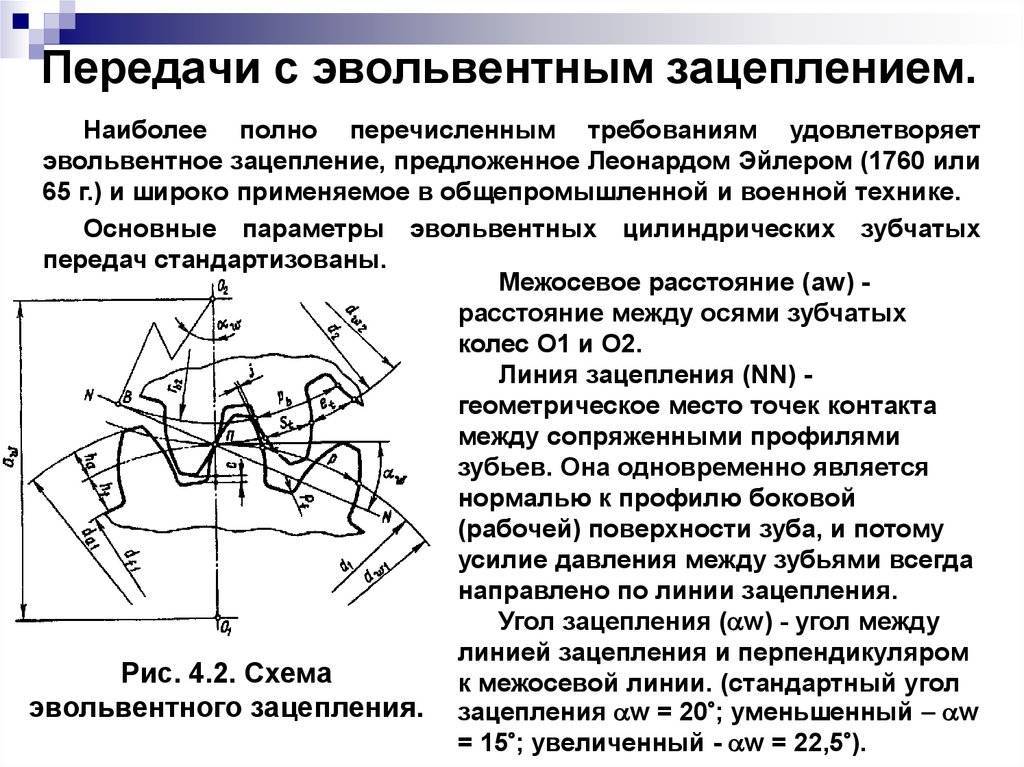
Основные параметры зубчатых цилиндрических передач

Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым

Межосевые расстояния

1 ряд	40	50	63	80	100	125	—	160	—	200	—	250	—	315	—	400
2 ряд	—	—	—	—	—	—	140	—	180	—	225	—	280	—	355	—
1 ряд	—	500	—	630	—	800	—	1000	—	1250	—	1600	—	2000	—	2500
2 ряд	450	—	560	—	710	—	900	—	1120	—	1400	—	1800	—	2240	—

1-й ряд следует предпочитать 2-му

Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200	225	250	280	315
Тихоходная ступень	63	80	100	125	160	200	225	250	280	315	355	400	450	500
Быстроходная ступень	355	400	450	500	560	630	710	800	900	1000	1120	1250	1400	1600
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600	1800	2000	2240	2500

Коэффициент запаса прочности при работе зуба двумя сторонами

Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах

Материал колес и термо- обработка	Отливки стальные и чугунные без термо- обработки	Отливки стальные и чугунные с термо- обработкой	Поковки стальные нормали- зованные или улучшенные	Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая)	Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой	Стальные с объемной закалкой	Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др.	Чугунные и пласт- массовые колеса
Коэфф.	1,9	1,7	1,5	2,2	1,4 — 1,6	1,8	1,2	1 — 1,2

Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200
Промежуточная ступень	63	80	100	125	160	200	225	250	280	315
Тихоходная ступень	100	125	160	200	250	315	355	400	450	500
Быстроходная ступень	225	250	280	315	355	400	450	500	560	630
Промежуточная ступень	355	400	450	500	560	630	710	800	900	1000
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600

Номинальные передаточные числа

1 ряд	1,0	—	1,25	—	1,6	—	2,0	—	2,5	—	3,15
2 ряд	—	1,12	—	1,4	—	1,8	—	2,24	—	2,8	—
1 ряд	—	4,0	—	5,0	—	6,3	—	8,0	—	10	—	12,5
2 ряд	3,55	—	4,5	—	5,6	—	7,1	—	9,0	—	11,2	—

1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5

Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25

Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.

При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.

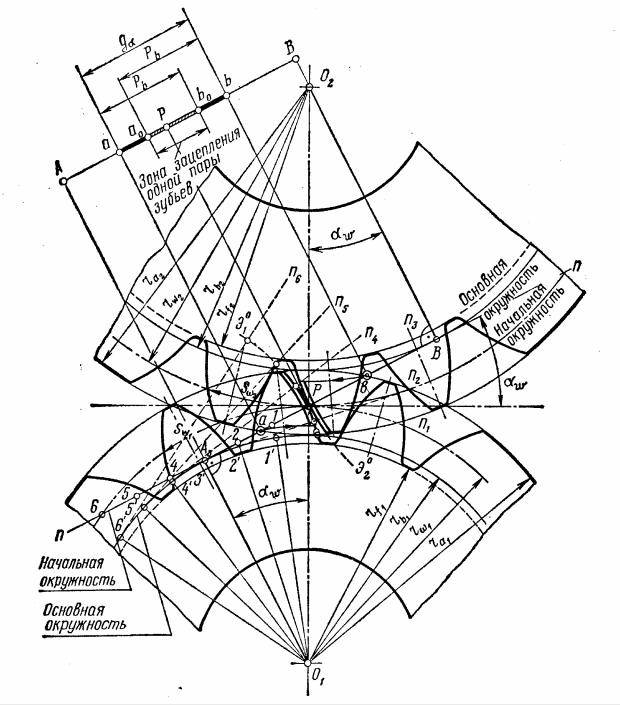
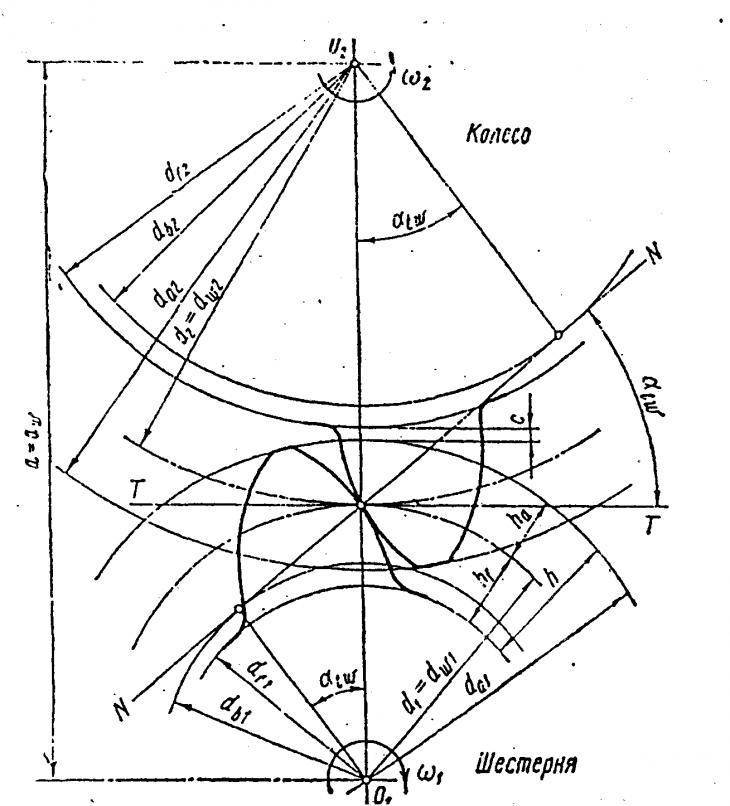
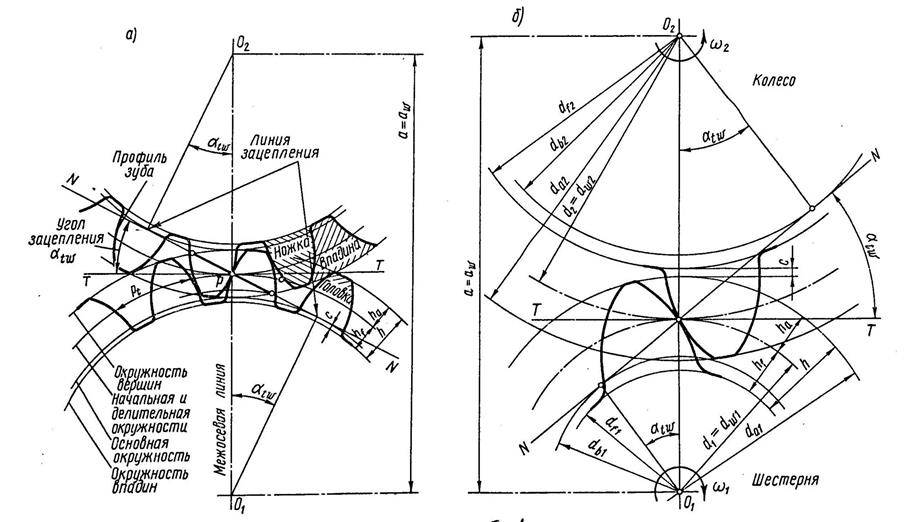
Построение эвольвентного зацепления

Существует несколько способов построения эвольвентного зацепления, используемого для изготовления зубчатых колес, которые можно выполнять вручную или с помощью систем автоматического построения.

При проектировании зацепления зубчатых колес учитывают не только геометрические параметры, но и технологические процесс изготовления, а также желаемые динамические и прочностные показатели готового механизма.

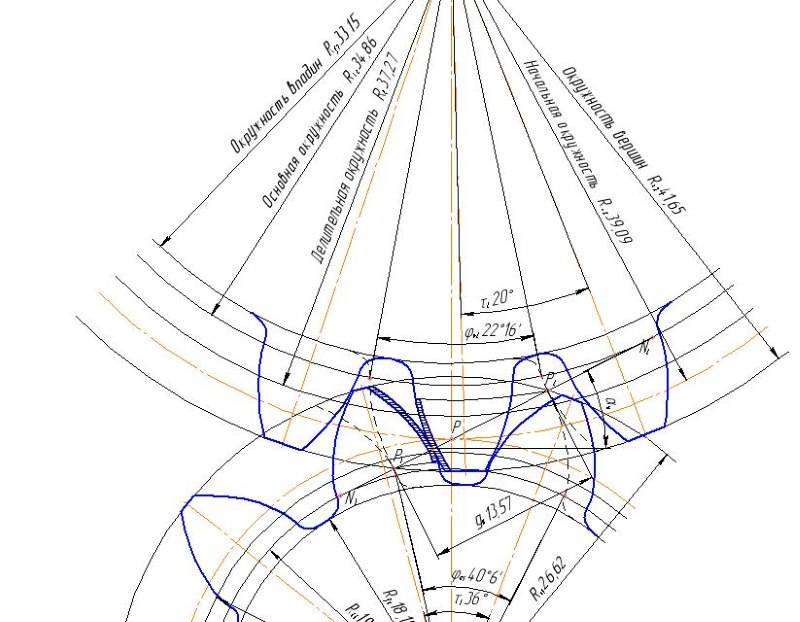
Построение эвольвенты зубчатого колеса состоит из нескольких этапов:

1. Графическое построение окружности радиусов (определяется исходя из необходимого количества зубьев и прочностных характеристик готового механизма).
2. Через полюс зацепления проводится прямая в токе касания изначальных окружностей (строится под необходимым углом зацепления).
3. Окружности колес должны соприкасается по полученной прямой. Обкатывание ее по окружности первого колеса, точка, совпадающая с полюсом, образует первую эвольвенту. Такая же манипуляция с колесом 2, позволяет получить вторую эвольвенту.

При производстве шестерен зубья несколькими методами: копирования и обкатки. Если необходимо изготовить мелкую деталь, прибегают к методу формообразования, другими словами – горячей накатки. Такой способ менее точен, но форма фрезы при копировании не позволяет выполнить миниатюрные вырезы.

Метод копирования предусматривает вращение фрезы вдоль поверхности, образующее зубья. Она прорезает одну впадину за один проход между соседними зубьями. Затем фреза возвращается в базовое положение с одновременным поворотом заготовки на необходимый угол шага. Такой способ изготовления довольно точный, но производительность его низкая.

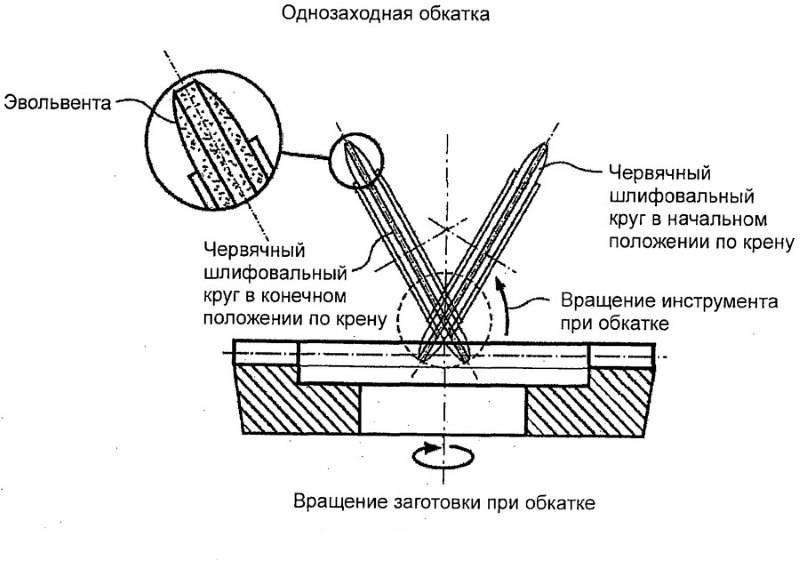
Более совершенным способом является метод обкатки. В его основе лежит огибающее движение, соответствующее желаемому движению зубчатого колеса при зацеплении. Процесс производства похож на движение шестерен в работе. Такое зацепление называется станочным. Рабочий инструмент в таком случае изготавливается в виде круглой, зубчатой фрезы или инструментной рейки.

Основные ошибки самостоятельной замены

Несмотря на предельно простую технологию, автолюбители часто допускают при замене венца следующие ошибки:

• перед тем, как снять зубчатый обод, следует произвести ревизию боковой плоскости маховика под сцепление, и отверстий для крепежных болтов;
• установка с перегревом отдельных участков венца приведет к быстрому износу зубьев именно на этих местах, так как происходит отпуск стали;
• наружный диаметр зубьев должен иметь фаску для плавного зацепления с бендиксом стартера без ударов.

Для того, чтобы уменьшить износ двигателя и увеличить приемистость машины на высоких оборотах, маховик часто облегчают. Из-за наличия дополнительных отверстий на наружном диаметре диска в зоне, примыкающей к зубчатому ободу, венец часто приваривается к диску.

Таким образом, венец можно заменить собственными силами при значительной выработке профиля зуба на отдельных участках. Снять обод можно на холодную, а при установке потребуется нагрев до 200 градусов максимум.

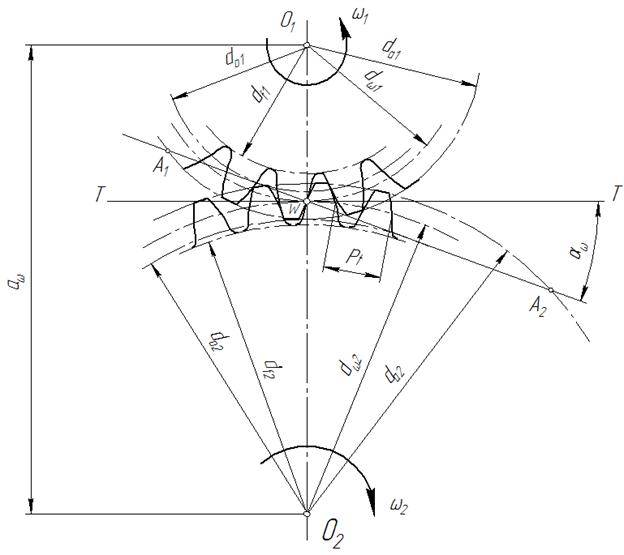
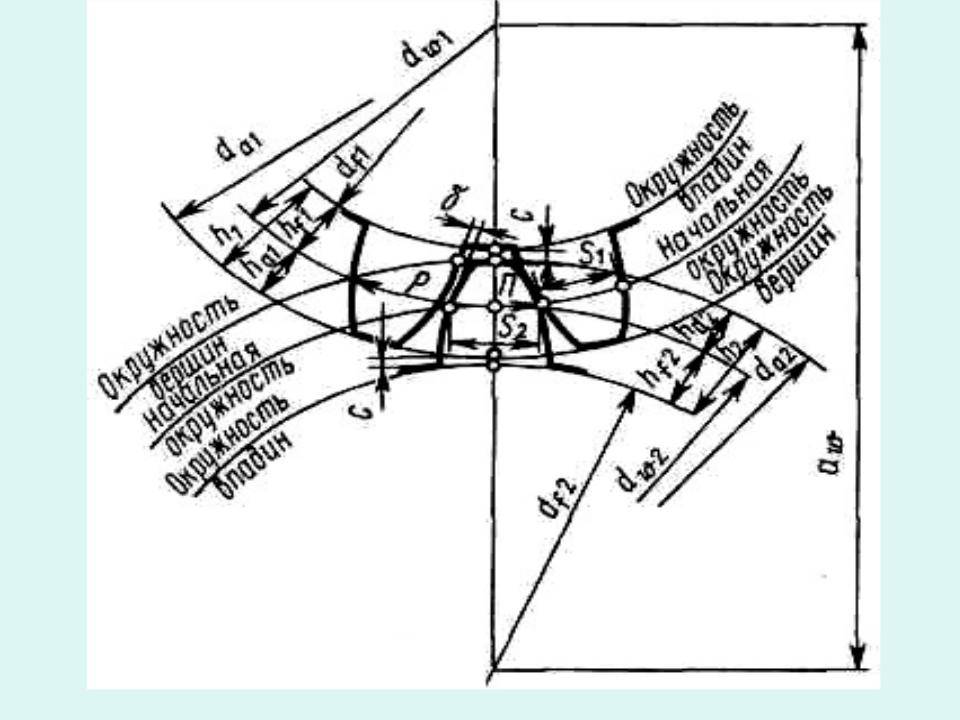
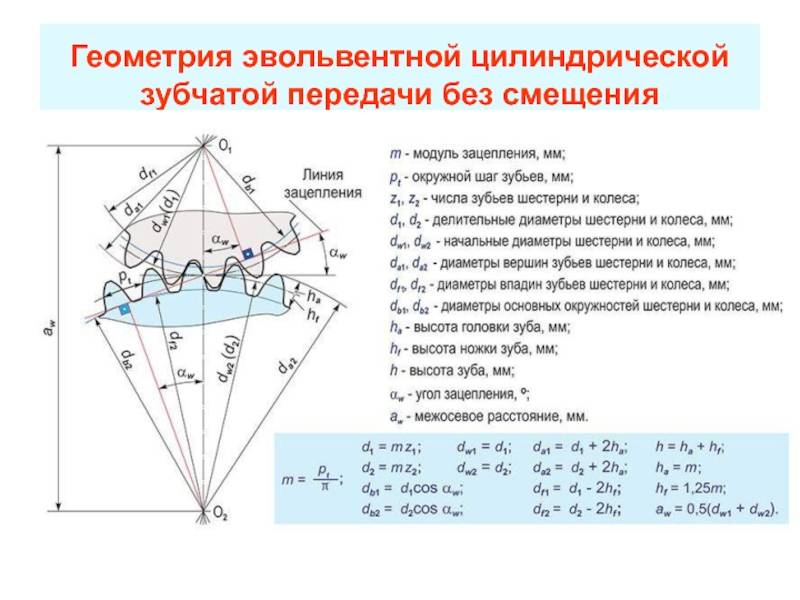
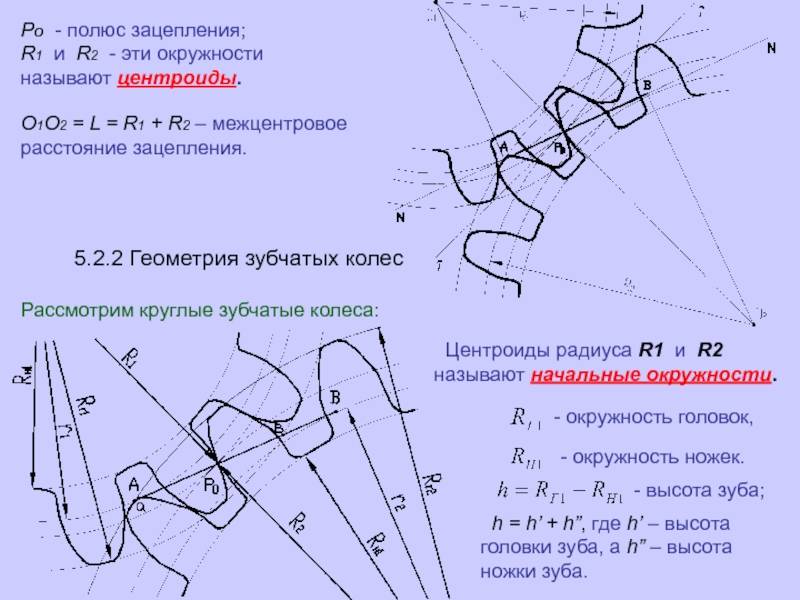
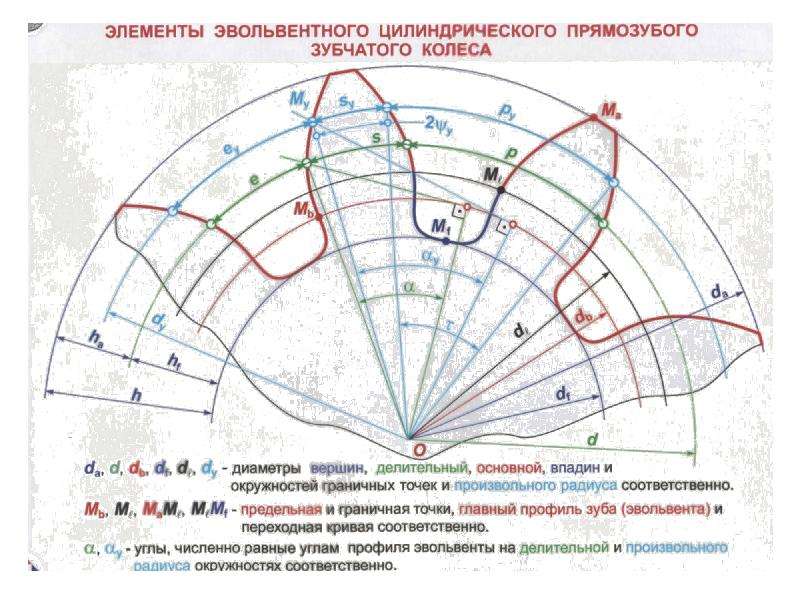
Геометрические параметры

Построенные проекта будущего колеса начинается с расчета его параметров.

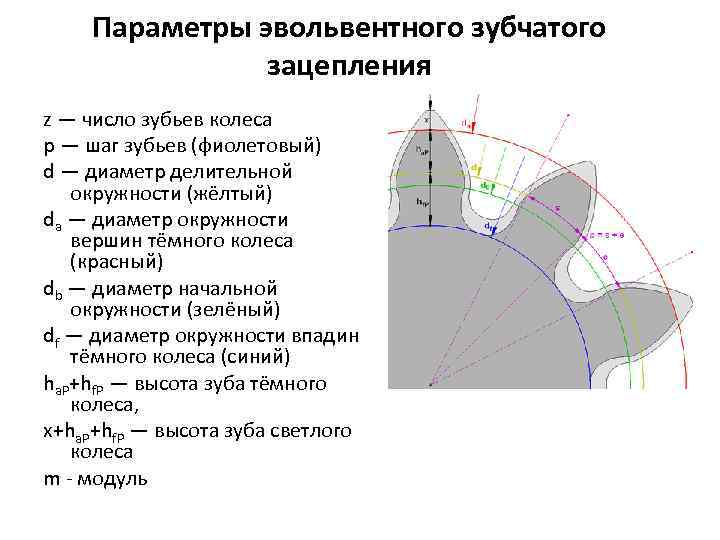
Рассмотрим параметры эвольвентного зацепления:

• шаг;
• модуль;
• число зубьев;
• угол профиля;
• коэффициент смещения.

Шаг бывает двух видов:

1. Окружной — длина между равнорасположенных точек на соседних зубьях.
2. Угловой – центральный угол, характеризрующий дугу делительной окружности.

Модуль — диаметр круга шестерни в миллиметрах, измеряемый к одному зубу. Делится на три вида: начальный (показатель окружности колеса начальной поверхности), основной и делительный (окружность колеса со стандартными значениями модуля и шага).

Число зубьев может быть разное, и зависит от диаметра шестерни, технических параметров и свойств готового механизма. К их параметрам можно отнести:

• толщина зуба;
• ширина впадины;

Угол профиля определяется между определенной точкой зуба, которая лежит на делительной окружности шестерни и вектором, прочерченным к точке от центра круга.

Подобное сцепление используется в различных сферах. Его легко встретить в машиностроении (в коробках передач автомобилей, в строительной, военной, сельскохозяйственной технике, судостроении, гидронасосах, лебедках и часовых механизмах).

На сегодняшний день можно найти множество разновидностей подобных шестерен, которые имеют различные свойства и геометрию

При выборе зубчатых колес в первую очередь нужно обращать внимание на прочность и шумовые характеристики

Особого внимания требует твердость метала, что особо важно для нормальной работы соответствующего механизма

История

Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.

В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.

Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.

Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .

Стандарты зубчатых передач США

Вместо модуля для стандартизации зубча­тых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диа­метра делительной окружности или диамет­ральный модуль (питч) (Р):

Р = z/d = z/(z • m/25,4) =25,4/m

Для перевода стандарта США в европейский стандарт служит зависимость:

m = 25,4 мм / P

Размещение зубьев в пределах диаметраль­ного модуля называется окружным шагом зацепления (CP):

CP = (25,4 мм / P) π.

Табл. Стандарты зубчатых передач

Полная высота зуба

В стандартах США полная высота зуба обо­значается как высота головки h_a = т, что соответствует величине т в стандартах Гер­мании.

Ножка зуба

Обозначается так же, как и полная вы­сота зуба, но расчет головки зуба основы­вается на использовании своего модуля. Пример обозначения:

Обозначение (пример): Р 5 /7

Р = 7 для расчета головки зуба,

Р = 5 для расчета других параметров.

Система обозначений и преобразований

Диаметр окружности выступов: OD = d_a.

Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).

Диаметр окружности впадин: RD = d_f

Начальный диаметр:

LD =(N+2x) / P (в дюймах)

или

LD= (N+2x)·m (в мм).

LD ≈ d_w,

где d_w — диаметральный модуль.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

• для отлитых зубцов: sв=πm-1,53m=1,61m:
• для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

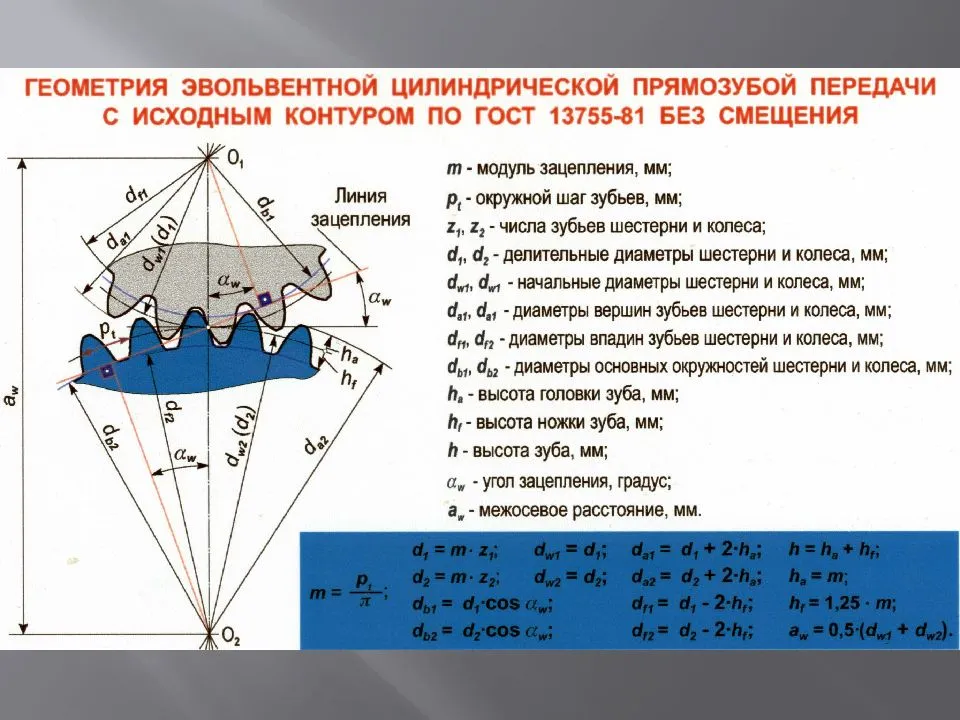
Геометрический расчет элементов цилиндрической зубчатой передачи

Исходные данные для расчета:

• Модуль m = 4 мм;
• Число зубьев шестерни Z1 = 18;
• Число зубьев колеса Z2 = 30;
• Диаметр вала (ведущий) DB1 = 22 мм;
• Тип шпонки – Призматическая;
• Число шлицев Z – 8;
• Внутренний диаметр шлицев d = 22 мм;
• Диаметр вала (ведомый) DB2 = 30 мм;
• Ширина шлица b = 6 мм;
• Тип – D.

Результаты геометрического расчета цилиндрической зубчатой передачи

• Делительный диаметр шестерни d1=mz1=4×18=72 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Высота головки зуба ha=m =4 мм;
• Высота ножки зуба hf=1,25m=1,25×4=5 мм;
• Высота зуба h=ha+hf=2,25m=2,25×4=9 мм;
• Диаметр вершин зубьев шестерни da1=d1+2ha1=72+2×4=80 мм;
• Диаметр впадин шестерни df1=d1-2hf=72-2×5=62 мм;
• Длина ступицы шестерни Lст1=1,5DB1=1,5×22=33 мм;
• Наружный диаметр ступицы шестерни Dст1=1,6DB1=1,6×22=35,2 мм;
• Диаметр вала шестерни D1=1,2×22=26,4 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Диаметр вершин зубьев колеса da2=d2+2ha=120+2×4=128 мм;
• Диаметр впадин колеса df2=d2-2hf2=120-2×5=110 мм;
• Длина ступицы колеса Lст2=1,5DB2=1,5×30=45 мм;
• Наружный диаметр ступицы колеса Dст2=1,6DB2=1,6×30=48 мм;
• Диаметр вала колеса D2=1,2DB2=1,2×30=36 мм;
• Ширина зубчатого венца b=6m=6×4=24 мм;
• Толщина обода зубчатого венца δ1=2,25m=2,25×4=9 мм;
• Толщина диска δ2=1/3b=8 мм;
• Межосевое расстояние a=0,5(d1+d2)=0,5(72+120)=96 мм;
• Длина шлицев Lшл=(1,5. 2)Lст2=(1,5. 2)45=72 мм.