Деформация изгиба

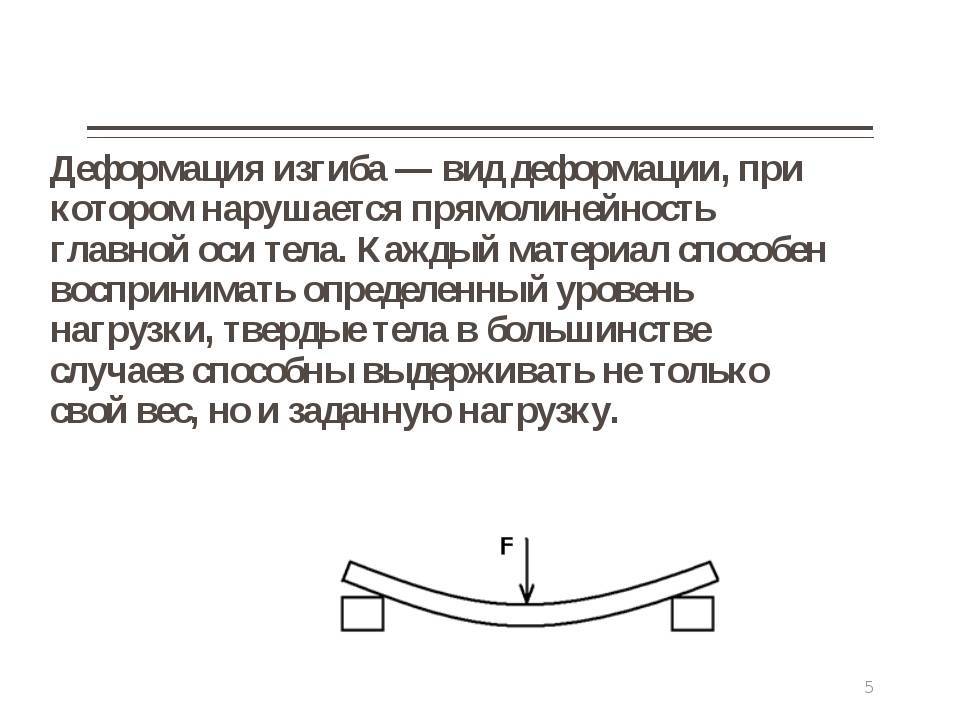
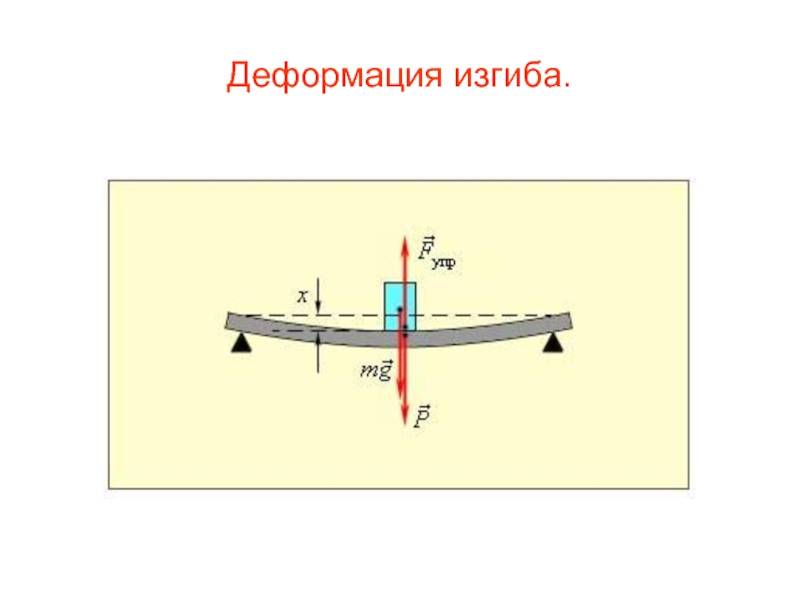
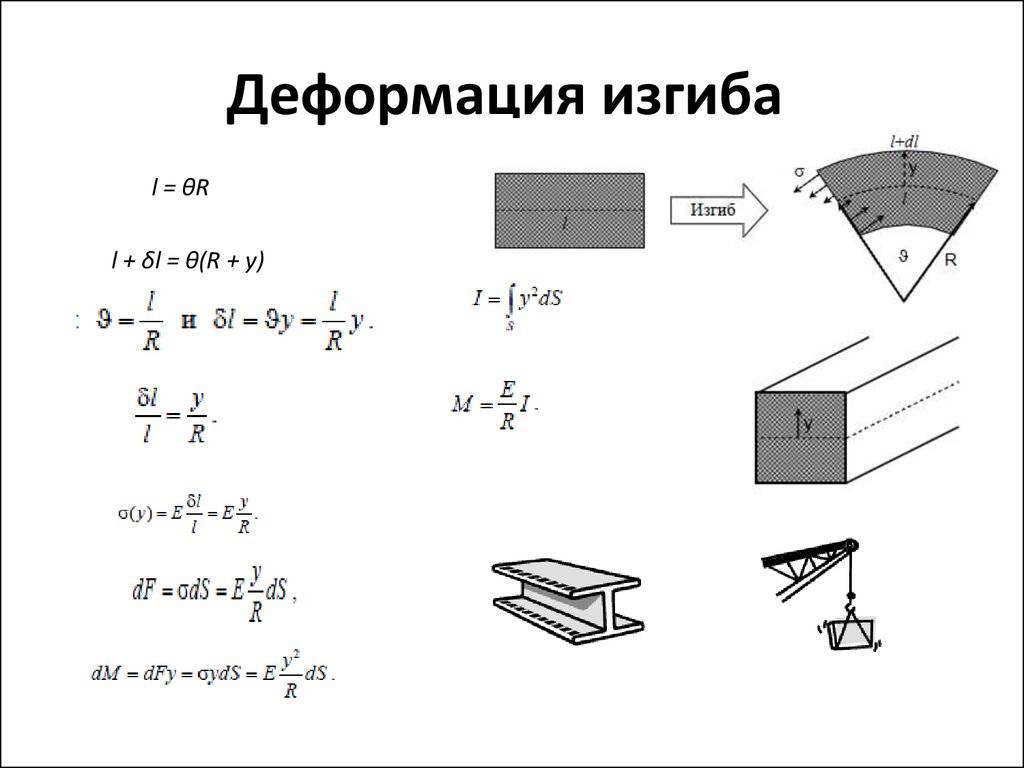
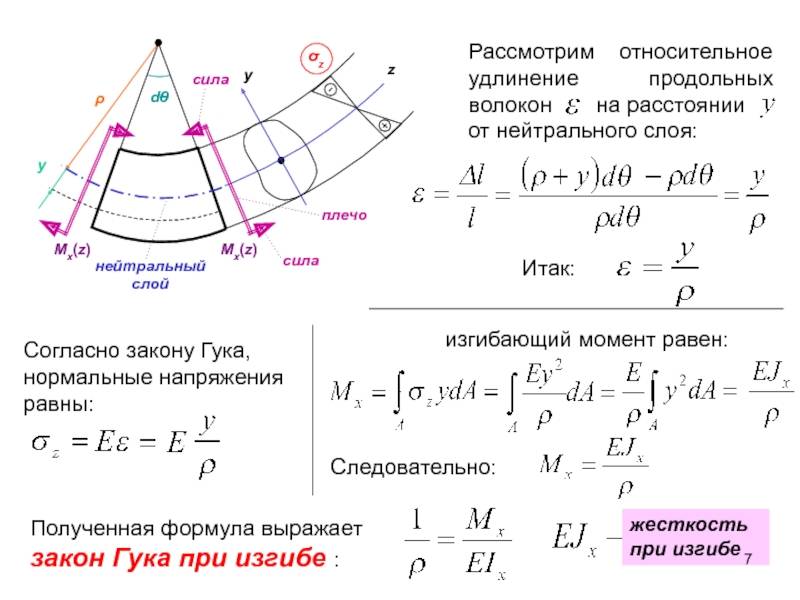
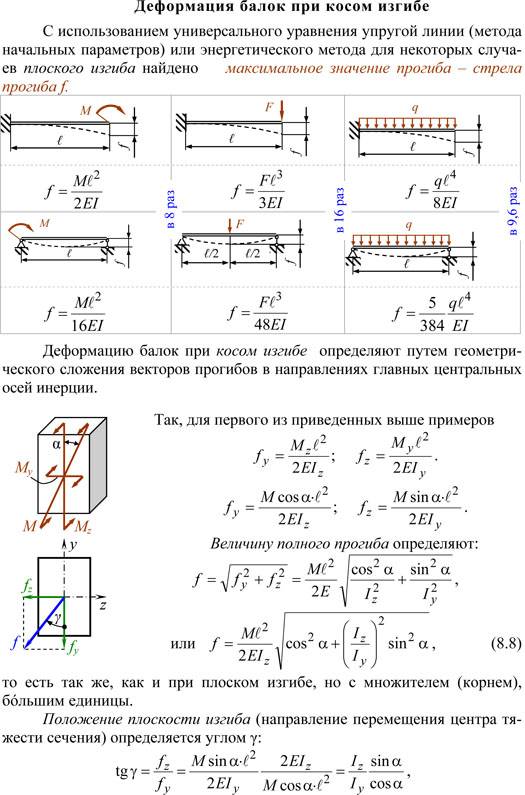
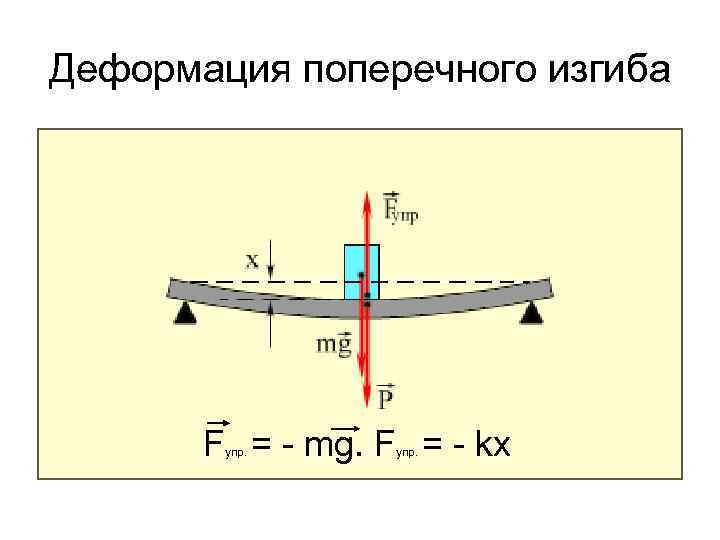
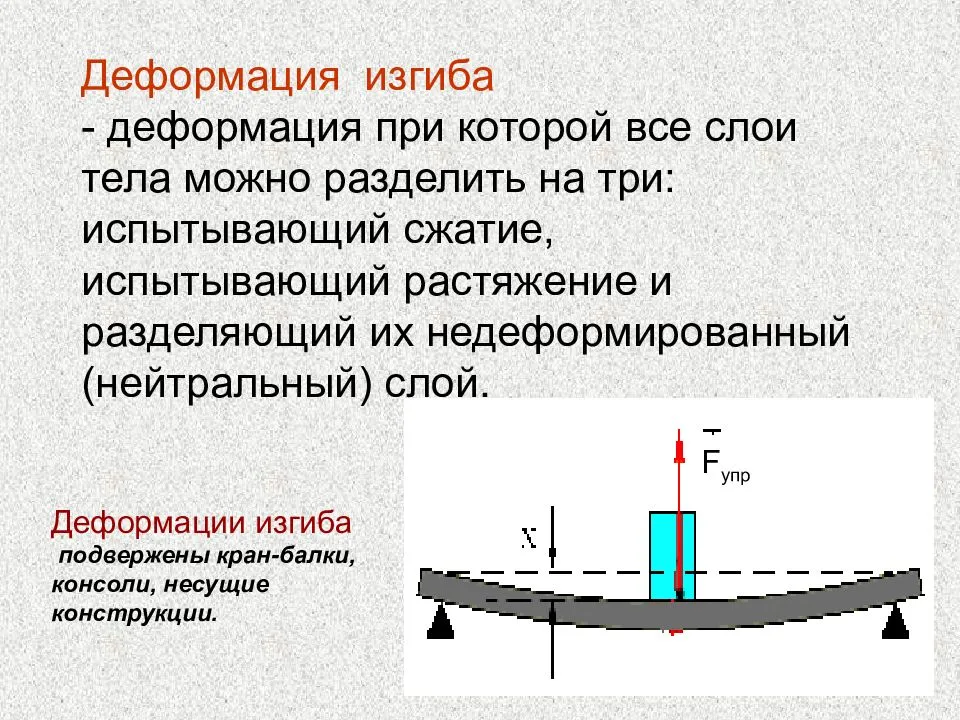
Последствия напряжения сварного шва

Последствия напряжения различают и по характеру деформации — упругая поверхностная может быть устранена или постепенно сойдет сама в процессе остывания. Пластическая деформация шва необратима, устранить ее без переваривания практически невозможно, при этом изменяется структура металла и его прочностные свойства.

Равномерность распределения

При оценке деформации используется коэффициент неравномерности, который позволяет учесть направление сил напряжения и заранее принять профилактические меры. Например, неравномерность будет выраженной, если часть заготовки контактирует с массивными холодными тисками, фиксируется ими, а при остывании именно в этой зоне формируется зона наибольшего напряжения. Имеет значение и разница в габаритах деталей — больший размер связан с изменением динамики нагрева и остывания, при соединении с фрагментом меньшего размера возникает неравномерно распределенное усилие.

Измерение деформации

При проектировании и эксплуатации различных механизмов, технических объектов, зданий, мостов и других инженерных сооружений очень важно знать величину деформации материалов. Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами

Для этого используют приборы, называемые тензометрами

Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами.

Тензометр состоит из тензометрического датчика и индикаторов. В него также может быть включено регистрирующее устройство.

В зависимости от принципа действия тензометры бывают оптические, пневматические, акустические, электрические и рентгеновские.

В основу оптических тензометров положено измерение деформации нити из оптоволокна, приклеенной к объекту исследования. Пневматические тензометры фиксируют изменение давления при деформации. В акустических тензометрах с помощью пьезоэлектрических датчиков проводятся измерения величин, на которые изменяются скорость звука и акустическое затухание при деформации. Электрические тензометры вычисляют деформацию на основе изменений электрического сопротивления. Рентгеновские определяют изменение межатомных расстояний в кристаллической решётке исследуемых металлов.

Вплоть до 80-х годов ХХ века сигналы датчиков регистрировались самописцами на обыкновенной бумажной ленте. Но когда появились компьютеры и начали бурно развиваться современные технологии, стало возможным наблюдать деформации на экранах мониторов и даже подавать управляющие сигналы, позволяющие изменить режим работы тестируемых объектов.

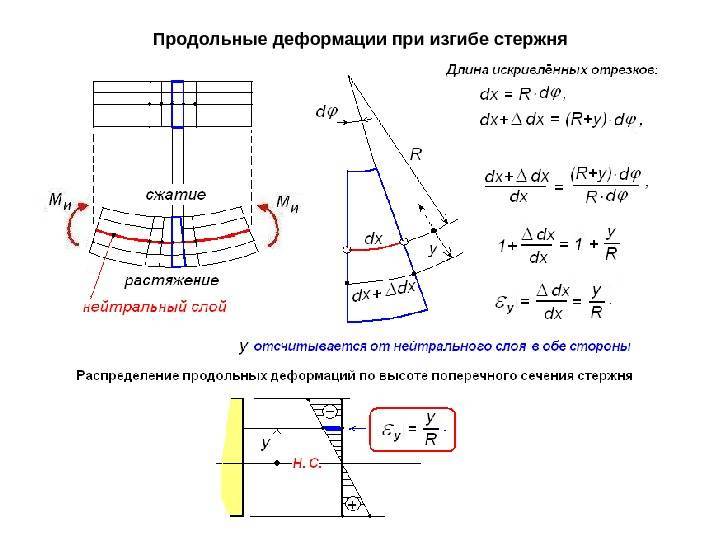
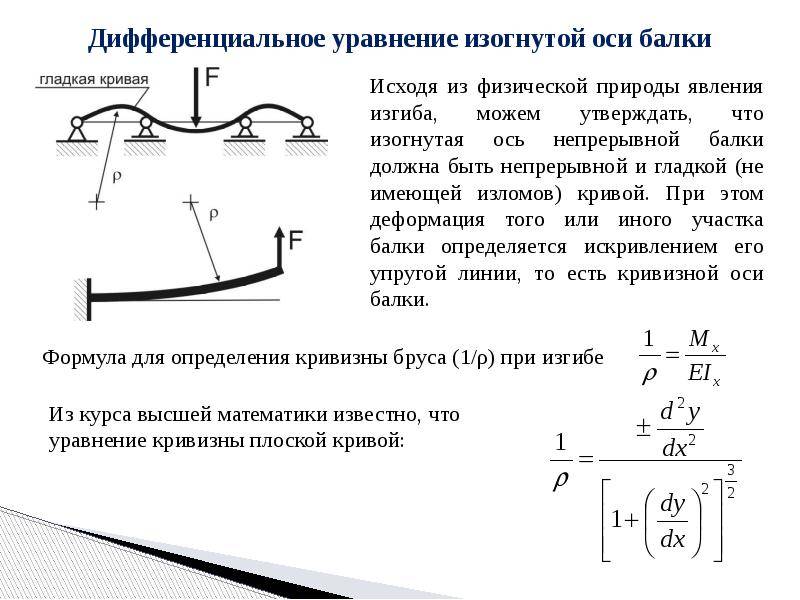
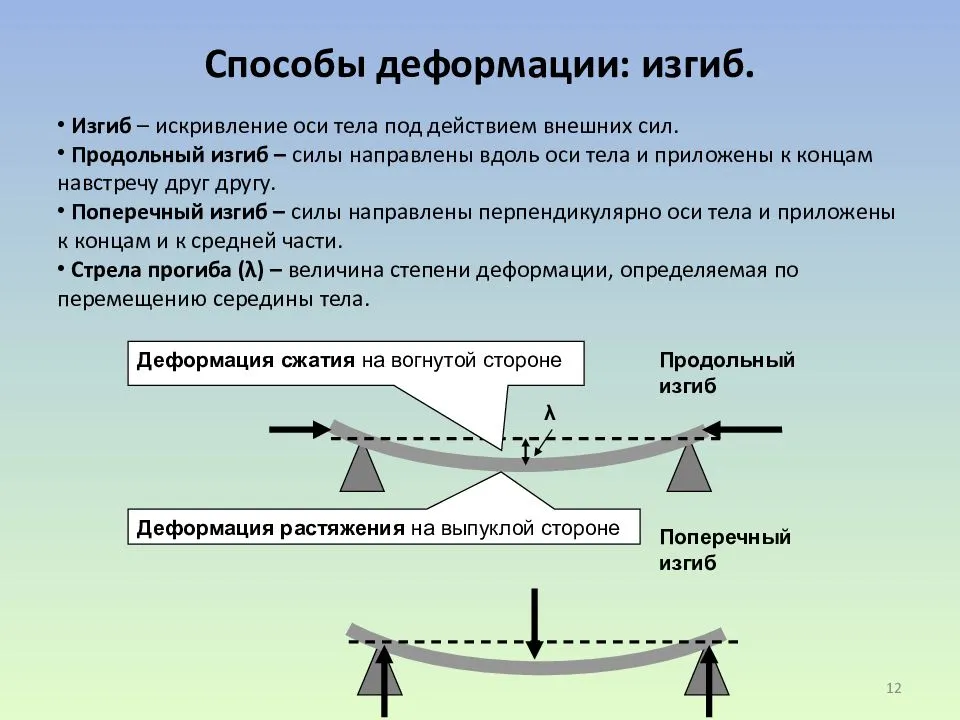
Чистый и поперечный изгиб балки

Если единственным внешним влиянием считается сила, вызывающая изгибающий момент, такой изгиб именуется чистым. Своей тяжестью изделия можно пренебречь.

При изгибе балки вводят следующие допущения:

• Во всех сечениях присутствуют только нормальные напряжения.
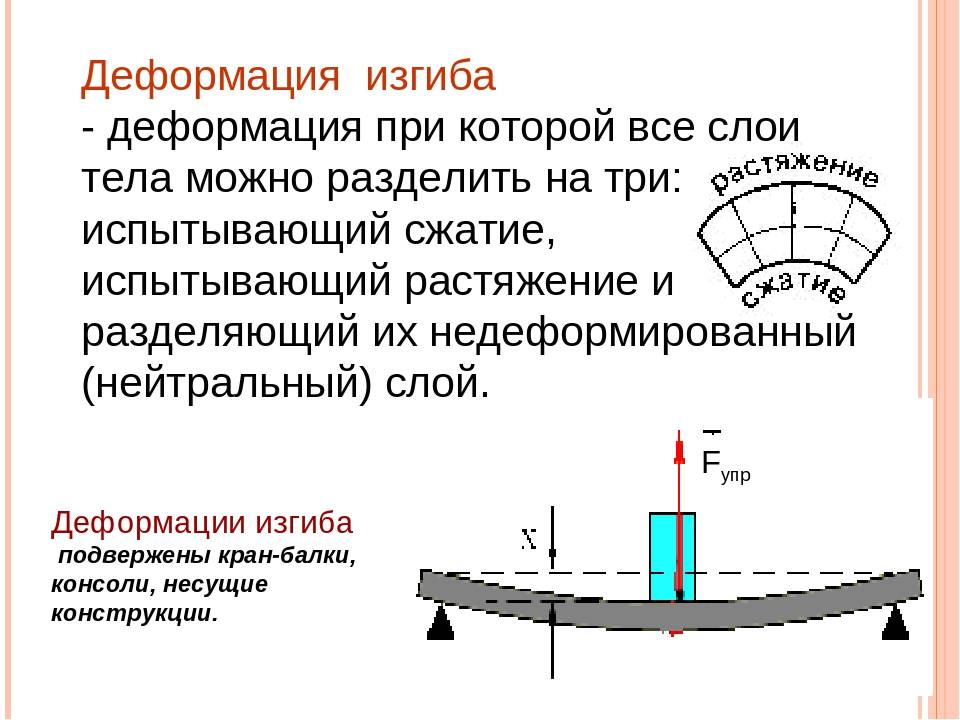
• Их разбивают на 2 слоя. Один называются растянутым, другой сжатым. Границей данных зон считается линия сечения. Величина нормальных стрессов нейтрального слоя равны нулю.
• Продольный компонент детали подвергается осевому напряжению. Оно вызывает растяжение или сжатие. Соседние слои не вступают во взаимное действие между собой.
• При сохранении геометрической формы лицевого слоя все слои внутри берегут былую форму. Влияние внешней силы остаётся перпендикулярным к поверхности детали.

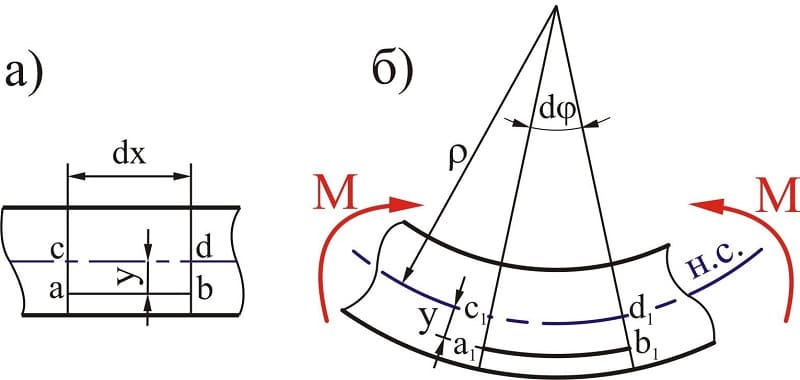
Если на поверхность детали выполняется влияние под угол к поверхности — такой изгиб именуется поперечным. При поперечном изгибе в слоях детали (к примеру, балки) появляются несколько видов стрессов. Одни называются нормальными, прочие касательными. В данном случае все сечения не будут плоскими, но искривлёнными. На конкретных уровнях искревления при изгибе не довольно большие. Это дает возможность при расчёте использовать все формулы, справедливые для чистого изгиба.

Расчёты на крепость при сдвиге

Оценка характеристик прочности изделий выполняется для определения наступления трёх факторов деформации:

1. Смещение некоторых слоёв (возникновения угла деформации).
2. Смятие крепежных элементов.
3. Сдвиг.
4. Разрыв.

Расчёт на крепость нужен для определения условий наступления любого из видов. В работе для более наглядной оценки параметров прочности и стойкости к деформированию решают существующие аналитические выражения и изображают эпюры отражающие направления влияния разных видов стрессов.

Получение численных параметров возможно благодаря использованию разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений изготавливается на основе принятых гипотез.

Расчёт возможных стрессов изготавливается на основании первой, третьей и четвёртой гипотезы прочности. Любая из гипотез принимается для различных материалов, которые обладают собственными физико-механическими свойствами.

Крепость быть на каждом из этапов разработки определенной детали. В первую очередь вычисляют величины возможных стрессов и угол отклонения на предварительном (проверочном) шаге. Это дает возможность определить их уровни, величины и направление приложенных сил. После чего приступают к проектированию. На данном шаге выполняется подбор материала детали и элементов крепежа с учитыванием достаточной прочности любого элемента конструкции. На конечном шаге ещё один раз проверяют возможные нормы нагрузки и способность готовой детали держать допустимую и дополнительную нагрузку, другими словами формируют прочностный запас.

Наиболее показательными являются расчёты для чистого сдвига. В данном случае при расчёте рассматривают следующие моменты выполнения задачи:

• Статический (составляется уравнение равновесия). В данном случае применяется предположение о равномерности распределения касательных стрессов. Впрочем в определенных случаях они делятся не одинаково, что затрудняет решение установленной задачи. Он дает возможность установить связь возникших стрессов с действующими внешними силами. Это выполняться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
• Геометрический (деформационный). Позволяет отобразить связь между отдельными маленькими участками исследуемой детали.
• Математический. Дает возможность подобрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
• Физический. Устанавливает связь между физическими процессами при деформации с учитыванием физических параметров материала и возникшими напряжениями (механическими качествами).

На математическом и физическом шаге рассмотрения установленной задачи используются следующие главные расчетные выражения и допущения:

• закон Гука для деформации смещения;
• гипотезы прочности (с учитыванием физических и механических параметров материала который для него выбран);
• выбор системы равноценных стрессов;
• упрощения при изображении эпюр, отображающих направления действующих сил и возникших стрессов;
• принятие ключевых положений для случая чистого сдвига.

В первом варианте происходит пластическая дефармация детали, когда интенсивность возникших стрессов превосходит предел текучести материала который для него выбран. Размер подобной деформации зависят от характера и интенсивности действия внешних сил, прочностных показателей материала, изменения режима температур.

При интенсивности влияния, превышающем крепость материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (к примеру, крепежных изделий, заклёпок, втулок).

Разработанные методы расчёта прочности дают возможность проектировать и делать детали с заданием, превышающим этот предел. Это дает возможность значительно повысить прочность и долговечность всей конструкции. Сейчас разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с использованием созданных программных средств, которые дают возможность получить числовые характеристики прочности и выстроить графические изображения эпюр в формате 3D графики.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

Рекомендуемые файлы

FREE

Учебный план для ИУ3, ИУ4, ИУ5, ИУ6, ИУ7, РК 6, РЛ6, МТ4, МТ8, МТ11, СМ13 Физика FREE

Лекции 2, 6, 8 и 17 Юрасова Н. И. Физика

Ф-65 Физика

М-61 Физика

6.1.16 Физика

6.2.13 Физика

Опора допускает вращение, но устраняет поступательное движение. Возникшую реакцию можно разложить на две составляющие ¾ горизонтальную и вертикальную.

3. Жесткая заделка.

Такое крепление не допускает ни линейных, ни угловых перемещений. Реакция, возникающая раскладывается на вертикальную и горизонтальную и момент защемления (реактивный момент).

7.2. Определение внутренних усилий при изгибе. Правило знаков для изгибающих моментов и поперечных сил.

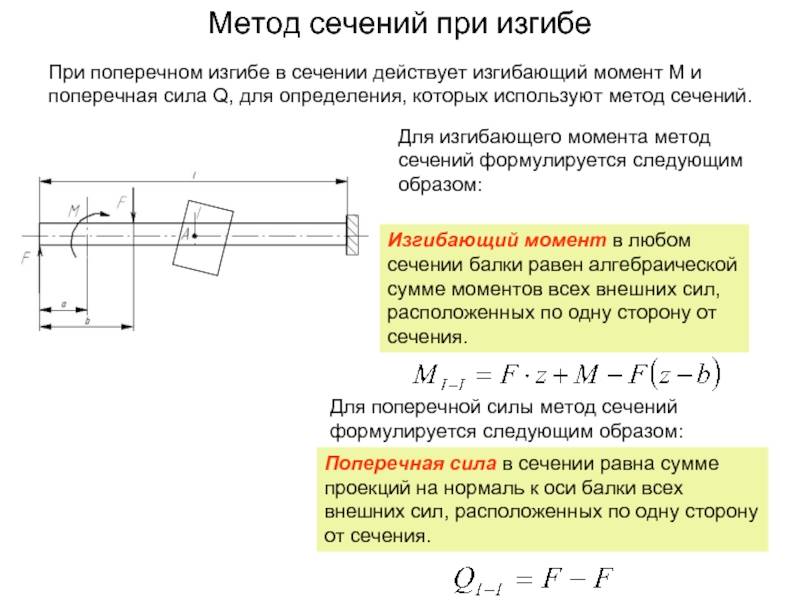
Для определения внутренних усилий при изгибе (изгибающий момент и поперечная сила) применим метод сечений.

Рассмотрим равновесие левой части.

Взаимодействие внутренних частей заменим внутренними усилиями: изгибающим моментом M_и и поперечной силой Q. Для их определения используем два уравнения равновесия.

1) SY=0; A-F₁+Q=0; Q=S(F_i)_y

2) SM=0; A_z-F₁(Z-Q)-M_и=0

      M_и=Sm(F_c)

Таким образом:

1) Поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих на одну сторону от сечения.

2) Изгибающий момент в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.

Поперечная сила в сечении балки считается положительной; если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа сверху вниз, и отрицательной в противном случае.

Изгибающий момент в сечении mn балки считается

положителным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, справа ¾ против. И отрицательным в противоположном случае.

Есть другое, более удобное для запоминания правило. Изгибающий момент положительный, если в рассматриваемом сечении балка изгибается выпуклостью вниз.

7.3. Построение эпюр изгибающих моментов и поперечных сил.

Рассмотрим пример:

Построить эпюры M_и и Q для балки на рис.

Проводим сечения Z₁ и Z₂. Изгибающий момент определим, взяв сумму моментов внешних сил справа от сечения

M_и=0

В сечении II-II

MZ₂=-F(Z₂ – a₂)

Знак минус потому что балка изгибается выпуклостью вверх.

Получили уравнение прямой

M_z2 = a₂ = 0

M_z2 = a₁ + a₂ = -F_a1                                          M_max=-F_a1 возникает у места заделки

Вычислим поперечную силу в сечении I-I. Проектируя на оси силы справа от сечения получим Q_z1=0. Тем же путем Q_z2=+F. Знак плюс взят т.к. внешняя сила справа от сечения направлена сверху вниз.

7.4. Определение нормальных напряжений. Условия прочности по нормальным напряжениям.

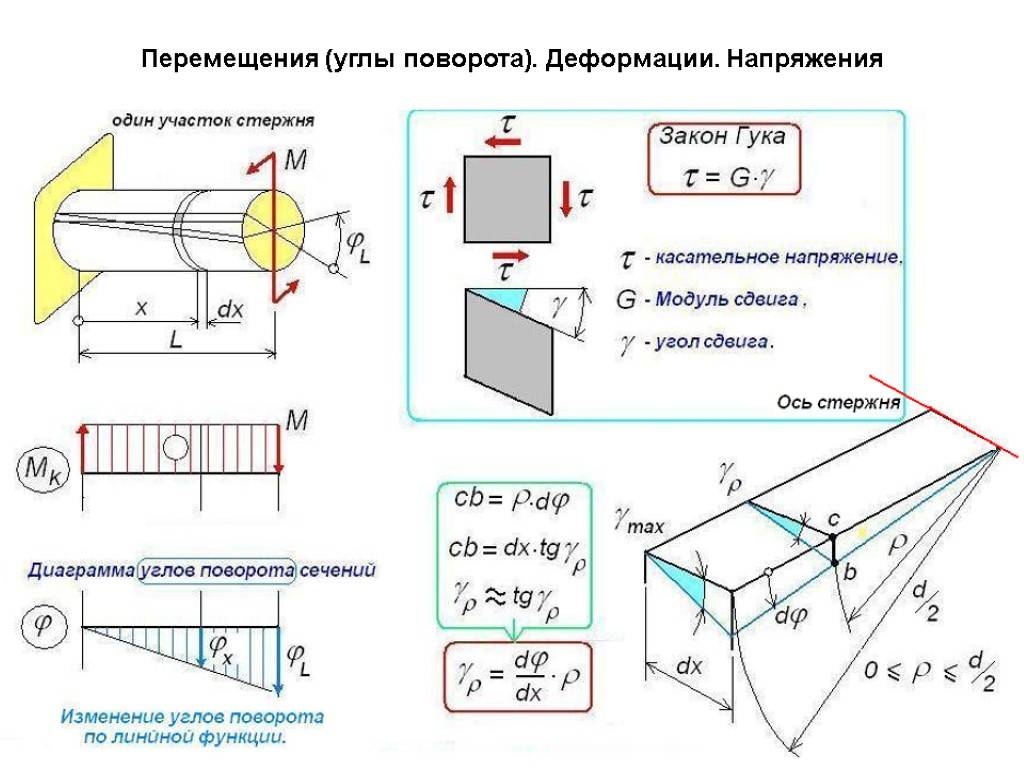
При деформации балки большие деформации испытывают более удаленные от нейтрального слой. Это слой, не испытывающий при изгибе ни растяжения ни сжатия.

Относительное удлинение волокна

e = Z / r

Z ¾ расстояние от нейтральной оси до рассматриваемого волокна.

r ¾ радиус кривизны нейтрального слоя

Тогда по закону Гука

s = Ee = E(Z / r)                     (1)

Можно также записать

M_и = EI_у / r,

где I_у = ò_AZ2dA ¾ представляет момент инерции сечения относительно нейтральной оси y. Откуда

1 / r = M_и / EI_у                                    (2)

K = 1 / r ¾ кривизна нейтрального слоя, т.е. кривизна оси балки при изгибе прямо пропорционально изгибающему моменту n и обратно пропорционально жесткости (Ei_у) балки. Подставляя (2) в (1) получим:

s = Z M_и / EI_у

Для обеспечения прочности балки необходимо, чтобы наибольшие растягивающие и наибольшие сжимающие напряжения при исгибе в опасном сечении не превосходили допускаемых.

Обозначив h_р и  h_с ¾ расстояния до наиболее удаленных растянутого и сжатого волокна запишем:

max s_р = M_иh_р / EI_у

max s_с = M_иh_с / EI_у

Для хрупких материалов допускаемые напряжения [s_с] > [s_р] в 3-5 раз. Поэтому для балок применяют сечения не симметричные относительно нейтральной оси. В указанном случае надо составлять два условия прочности:

max s_р = M_и / W_ур £ [s_р]

max s_с = M_и / W_ус < [s_с]

при симметричном сечении балки

s = (M_и / I_у)(h / 2) £

W_у = 2I_у / h ¾ осевой момент сопротивления.

Момент сопротивления является геометричесой характеристикой поперечного сечения балки, определяющей прочность при изгибе.

Значения W_у для простейших случаев:

а) прямоугольник

W_x = 2I_x / h = bh2 / 6

б) круг

W_x = 2I_x / d = pd42 / 64d = pd3 / 32 » 0,1d3

в) для кольца

W_x = (pD3 / 32) / (1-c4) = 0,1D3(1-c4)

Допускаемый изгибающий момент определяется

[M_и] £ W_x

7.5. Рациональные формы сечения балок.

Рекомендация для Вас – 4.4. Контроль за выполнением производственной программы.

Для количественной оценки рациональности сечения (при замере материала) служит безразмерная величина

w_x = W_x / ÖA3

это осевой удельный момент сопротивления. w_x зависит только от формы сечения

круг w_x  = 0,14

двутавр w_x  = 1,02-1,51

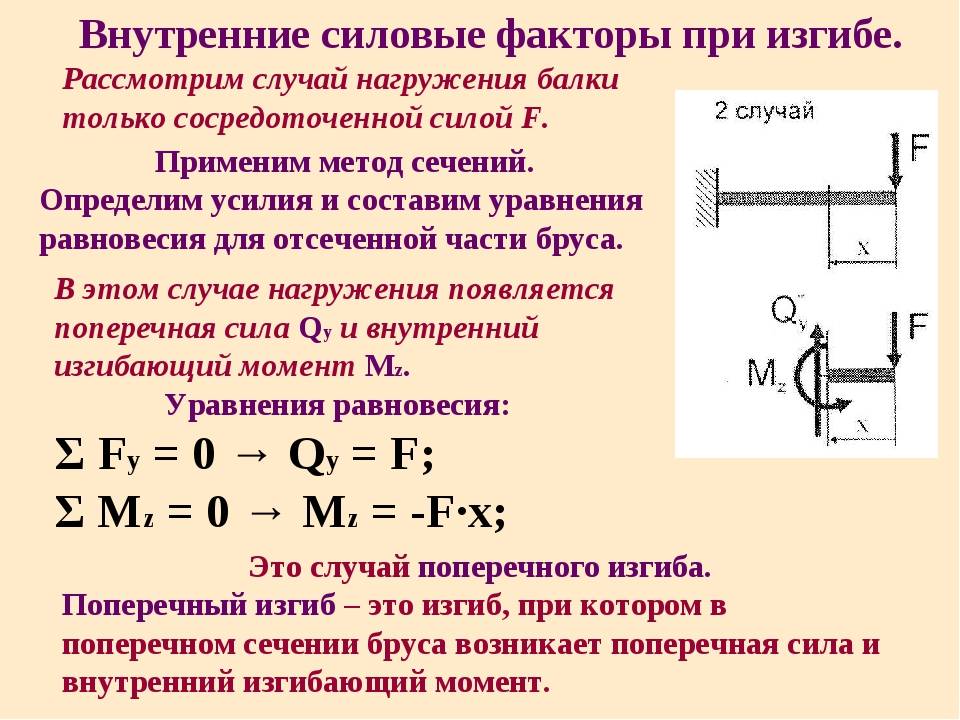
Внутренние силовые факторы при изгибе балки.

При плоском поперечном изгибе в сечениях балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М. Для их определения используют метод сечений (см. лекцию 1). Поперечная сила Q в сечении балки равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.

Правило знаков для поперечных сил Q:

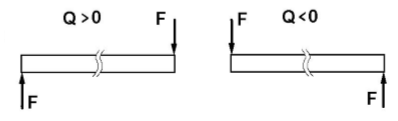
Изгибающий момент М в сечении балки равен алгебраической сумме моментов относительно центра тяжести этого сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.

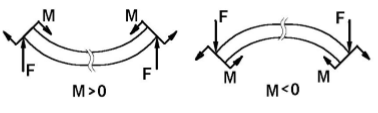
Правило знаков для изгибающих моментов M:

Сдвиг фаз переменного тока и напряжения

Мощность постоянного тока, как мы уже знаем, равна про­изведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При пере­менном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденса­торов и катушек индуктивности.

Для этого случая формула мощности

На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают)

Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы

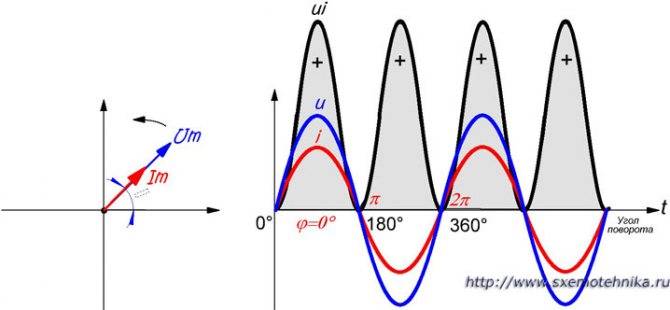
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.

При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.

О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.

Представим себе, что при начале вращения радиусы-век­торы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.

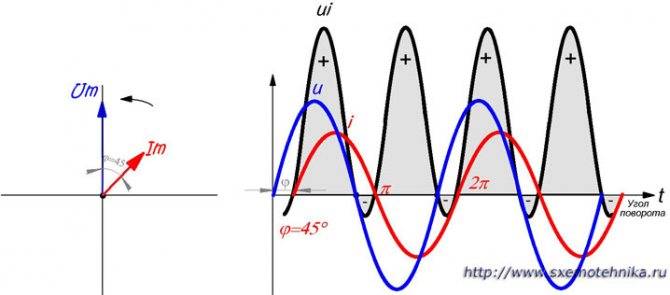
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.

Рассмот­рим, как будут изменяйся при этом ток и напряжение. Из по­строенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.

Затем напряжение достигает своей наибольшей ве­личины и начинает уже убывать, а ток хотя и становится по­ложительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направле­ние, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряже­ния. Между фазами напряжения и тока существует постоян­ный сдвиг, называемый сдвигом фаз.

Действительно, если мы посмотрим на рисунок 2, то заме­тим, что синусоида тока сдвинута вправо относительно сину­соиды напряжения. Так как по горизонтальной оси мы откла­дываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.

Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с на­правлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величи­ны на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источни­ком ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.

Прочность на изгиб цилиндра

Рассмотрим балку с простой опорой, у которой две равные нагрузки W / 2 действуют на расстоянии L / 3 от обоих концов.

Значение реакции в точках A и B можно рассчитать, применяя условия равновесия

Для вертикального равновесия

Принимая момент около A, момент по часовой стрелке положительный, а момент против часовой стрелки принимается как отрицательный.

Положив значение R_B в получаем

В соответствии с соглашением о знаках для ЮФО и ПРО

Сила сдвига в точке A

Сила сдвига при C

Сила сдвига в точке B

Для диаграммы изгибающего момента, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.

Изгибающий момент при A = M_A = 0

Изгибающий момент при C = [Вт / 2] * [L / 3] …………………………

Изгибающий момент при C =

Изгибающий момент при D =

Изгибающий момент при B = 0

Пусть d = диаметр цилиндрической балки, согласно уравнению Эйлера-Бернулли.

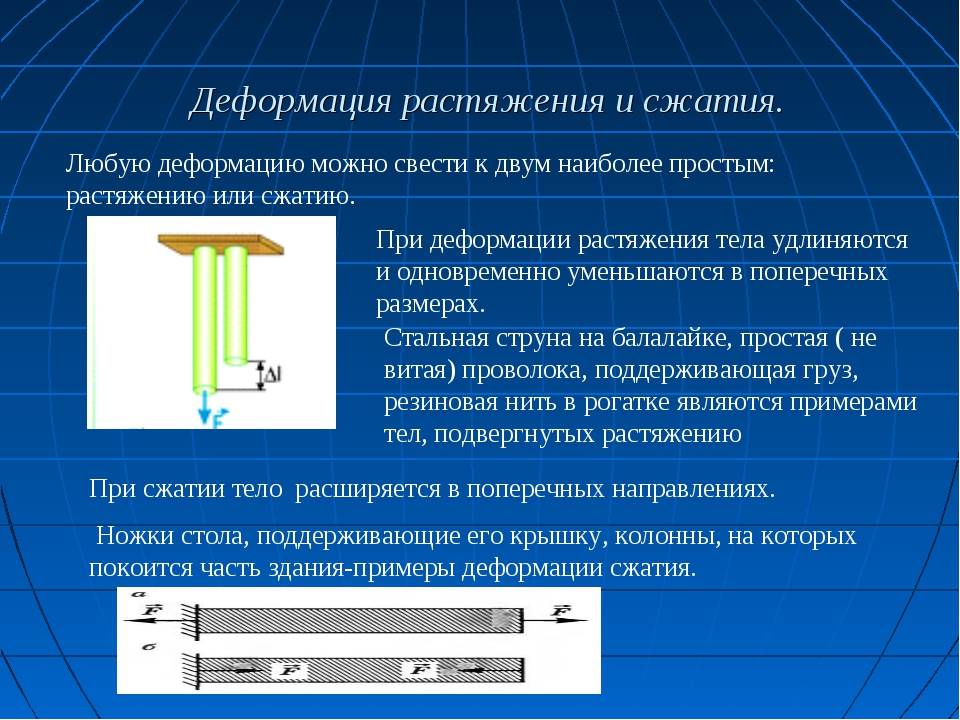
Продольные и поперечные деформации. Закон Гука

Иметь представление о продольных и поперечных деформациях и их связи.

Знать закон Гука, зависимости и формулы для расчета на­пряжений и перемещений.

Уметь проводить расчеты на прочность и жесткость ста­тически определимых брусьев при растяжении и сжатии.

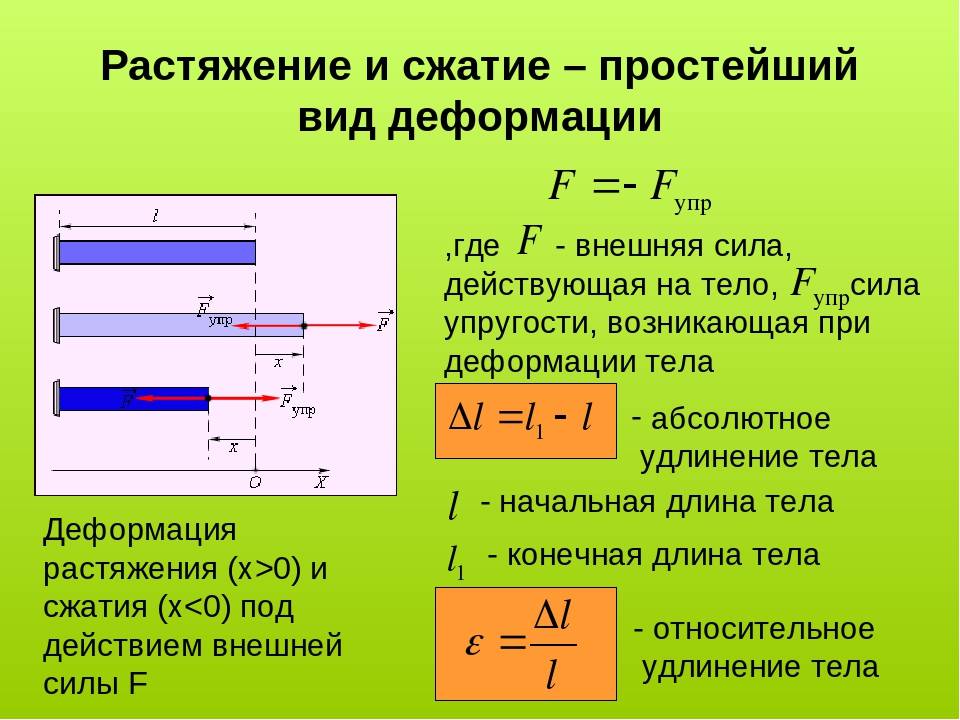
Деформации при растяжении и сжатии

Рассмотрим деформацию бруса под действием продольной силы F (рис. 4.13).

Начальные размеры бруса: — начальная длина, — начальная ширина. Брус удлиняется на величину Δl; Δ1— абсолютное удлинение. При растя­жении поперечные размеры уменьшают­ся, Δ а — абсолютное сужение; Δ1 > 0; Δ а 0.

В сопротивлении материалов приня­то рассчитывать деформации в относи­тельных единицах: рис.4.13

— относительное удлинение;

Относительное сужение.

Между продольной и поперечной деформациями существует зависимость ε′=με, где μ – коэффициент поперечной деформации, или коэффициент Пуассона, — характеристика пластичности материала.

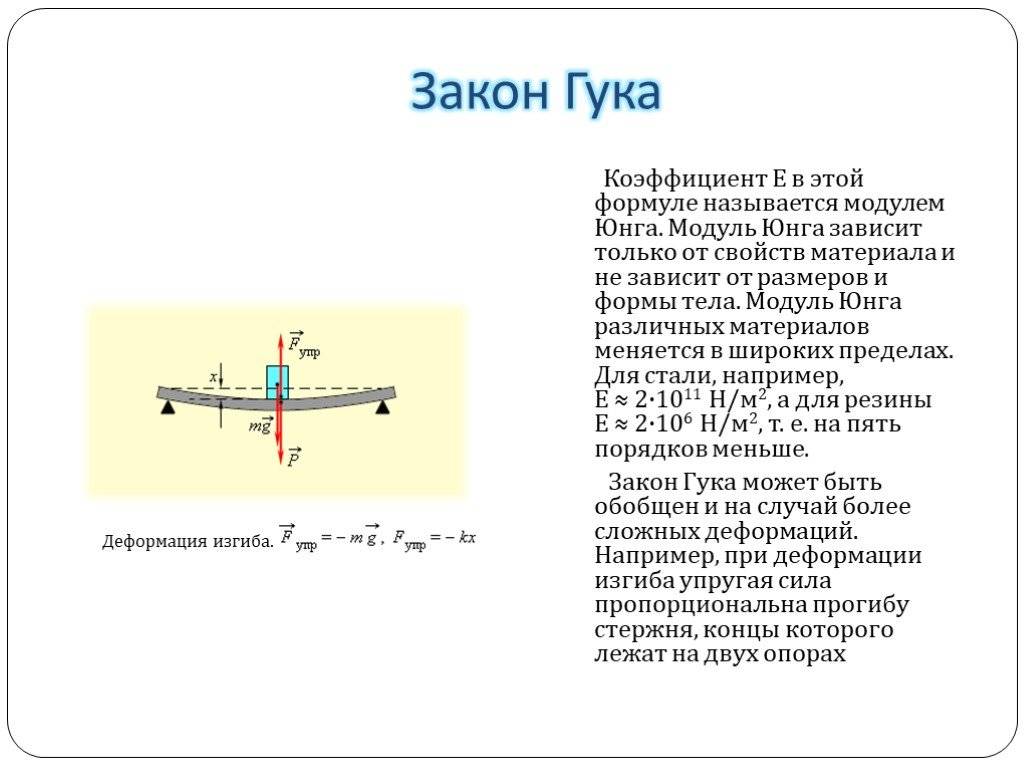
Закон Гука

Основной закон, рассматриваемый при деформации тела. Согласно ему, деформация, возникающая в теле, прямо пропорциональна воздействующей силе. Единственная оговорка заключается в том, что он применим только при малых значениях деформации, поскольку при больших значениях и превышении предела пропорциональности эта связь становится нелинейной. В простейшем случае (для тонкого растяжимого бруска) закон Гука имеет следующий вид:

Ф=к*Л,

где Ф – это приложенная сила; к – коэффициент упругости; Л – это изменение длины бруса.

Если с двумя величинами всё понятно, то коэффициент (к) зависит от нескольких факторов, таких как материал изделия и его размеры. Его значение также можно вычислить по следующей формуле:

к=(Е*С)/Л,

где Е – это модуль Юнга; С – площадь поперечного сечения; Л – длина бруса.

Что это такое?

Модуль упругости (модуль Юнга) – показатель, определяющий механическую реакцию материала. При помощи данного параметра удается охарактеризовать поведение образца при растяжении. Если говорить более простым языком, то модуль упругости означает пластичные свойства стали, и чем выше показатель, тем меньше растяжение. В теории модуль Юнга обозначают буквой «Е». Это один из компонентов закона Гука, в котором рассматриваются возможные деформации упругих тел. Посредством данной величины удается связать возникающие в материале напряжения с деформацией, которую он испытывает. Единица измерения модуля упругости – паскали (Па) или мегапаскали (МПа). Однако часто инженеры при проведении расчетов отдают предпочтение кгс/см2. Показатель определяют путем исследований в лабораториях, фиксируя образцы на специальном оборудовании. В основе методики лежит разрыв образцов в форме гантелей на автоматизированных установках.

В ходе эксперимента автоматика отслеживает показатели изменения длины и натяжения заготовки, при которых она разрушается, а затем делит результаты. Полученное число и будет модулем Юнга или модулем упругости. Примечательно, что подобная методика определения показателя используется для определения Е:

• стали;
• меди;
• других упругих образцов.

В хрупких материалах параметр определяют путем сжатия до момента появления трещин. Стоит подробнее остановиться на разборе модуля Юнга с точки зрения физики. В процессе принудительного нагружения, которое приводит к изменению формы материала, внутри него возникают ответные усилия. Силы начинают оказывать сопротивление напряжениям извне и стремятся вернуть форму тела. Если образец совершенно не реагирует на нагрузку (точнее, полностью меняет форму и не восстанавливает ее при снятии усилий), его принято считать пластичным. В качестве примера стоит назвать пластилин, который наглядно отражает теорию на практике. Исследованием упругости материалов занимался ученый Р. Гук, которого интересовало, как будут меняться и удлиняться стержни разных материалов под воздействием гирь. Благодаря ранее проведенной серии опытов удалось доказать, что величины абсолютного удлинения и исходной длины прямо пропорциональны. В то же время абсолютное удлинение обратно пропорционально площади поперечного сечения исследуемого стержня.

Гук вывел целый закон, а также ввел параметр Е для характеристики свойств упругого материала. Таким образом, физический смысл модуля заключается в том, что параметр соответствует напряжению, вызываемому в стержне при растягивании на длину, которая в два раза выше при условии отсутствия видимых разрушений образца.

Посредством модуля Е удается предугадать, как будет вести себя материал при определенных нагружениях. Однако он не дает понимания того, что с ним произойдет при других способах нагружения. Поэтому для проведения эффективных расчетов необходимо введение дополнительных параметров.

• Жесткость. Показатель демонстрирует степень пластичности узла исследуемого образца. Единица измерения параметра – кгс.
• Относительное удлинение в продольном направлении. При расчете используются два показателя: величина абсолютного удлинения и общая длина образца. Показатель не имеет единицы измерения, однако для упрощенного понимания его умножают на 100%.
• Относительное удлинение в поперечном направлении. Высчитывается таким же образом, как и предыдущий параметр, только вместо длины используют диаметр стержня-образца. Как показали испытания, поперечное удлинение обычно меньше продольного.
• Коэффициент Пуассона. Представляет собой соотношение двух последних показателей. Параметр делает возможным описание того, как материал будет менять свою форму, опираясь на величину нагрузки и место ее приложения.
• Модуль сдвига. С его помощью удается описать поведение материала с упругими свойствами при воздействии сил по касательной. Другими словами, помогает оценить работу конструкции при воздействии на нее ветра под углом в 90 градусов.