Потенциальная энергия пружины

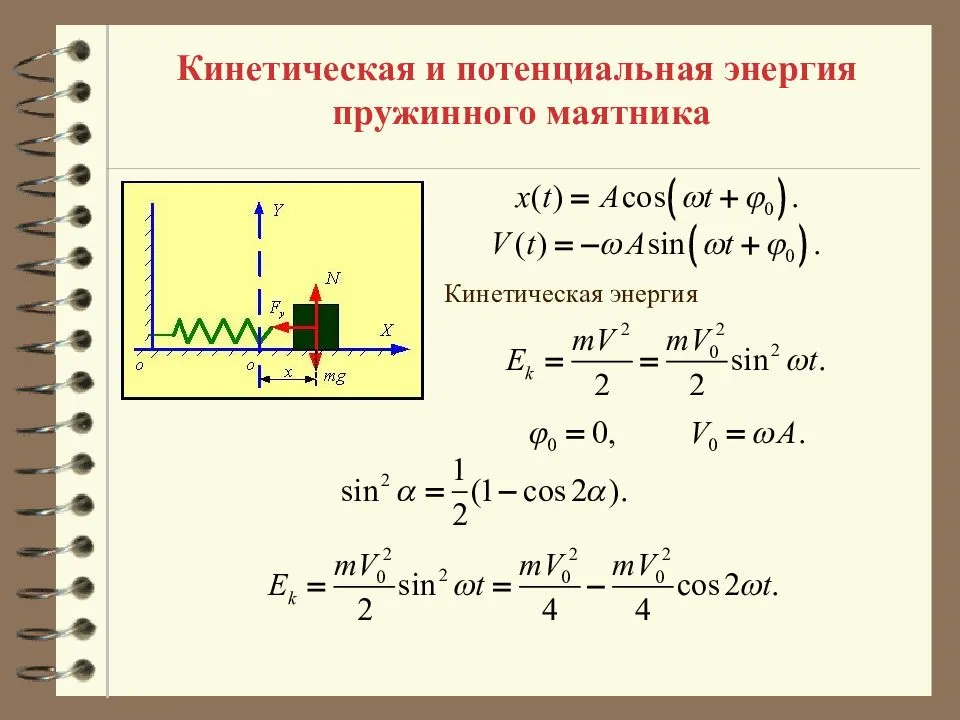
Энергия колебаний пружинного маятника

Рассматривая колебание груза на пружине нужно учитывать тот момент, что при движение маятника может описываться двумя точками, то есть оно носит прямолинейный характер. Этот момент определяет выполнение условий, касающихся рассматриваемой силы. Можно сказать, что полная энергия потенциальная.

Провести расчет энергии колебаний пружинного маятника можно при учете всех особенностей. Основными моментами назовем следующее:

1. Колебания могут проходить в горизонтальной и вертикальной плоскости.
2. Ноль потенциальной энергии выбирается в качестве положения равновесия. Именно в этом месте устанавливается начало координат. Как правило, в этом положении пружина сохраняет свою форму при условии отсутствия деформирующей силы.
3. В рассматриваемом случае рассчитываемая энергия пружинного маятника не учитывает силу трения. При вертикальном расположении груза сила трения несущественна, при горизонтальном тело находится на поверхности и при движении может возникнуть трение.
4. Для расчета энергии колебания применяется следующая формула: E=-dF/dx.

Приведенная выше информация указывают на то, что закон сохранения энергии выглядит следующим образом: mx2/2+mw2x2/2=const. Применяемая формула говорит о следующем:

1. Максимальная кинетическая энергия установленного маятника прямо пропорциональна максимальному значению потенциальной.
2. На момент осциллятора среднее значение обоих сил равны.

Провести определение энергии колебания пружинного маятника можно при решении самых различных задач.

Вопрос 16

Текст вопроса

BB2c18 В первой серии опытов по исследованию малых колебаний разных грузов на нити одинаковой длины использовался железный грузик, во второй – алюминиевый такого же объёма. Угол отклонения нити от вертикали в обоих исследованиях одинаковый.

Читать также: Индукционная печь что это

Как при переходе от первой серии опытов ко второй изменяется период колебаний, частота и максимальная кинетическая энергия груза?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Механические колебания. Пружинный маятник

Механическими колебаниями называются движения, характеризующиеся определенной повторяемостью во времени.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Гармоническими называются колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (или косинуса).

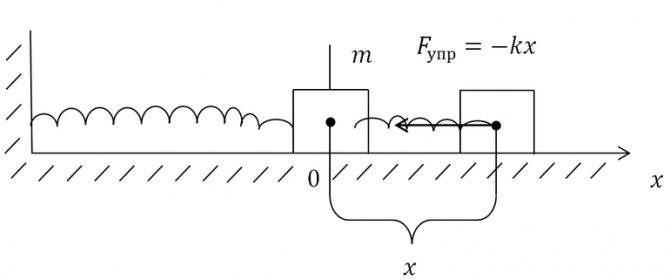
Пружинный маятник – это колебательная система, состоящая из груза массой т, закрепленного на пружине, совершающая гармонические колебания под действием упругой силы , зависящей от величины линейной деформации x по закону Гука (Fx= – kx, где k – жесткость пружины.

Согласно второму закону Ньютона уравнение движения маятника:

Так как ускорение a является второй производной от смещения x (), то

или .

Если обозначить , то получим дифференциальное уравнение свободных незатухающих гармонических колебаний пружинного маятника:

Решением этого дифференциального уравнения является функция x(t):

,

где – отклонение тела от положения равновесия в момент времени t;

А – амплитуда колебания, то есть максимальное отклонение колеблющегося тела от положения равновесия;

w0 – круговая (циклическая) частота;

(w0t+j0) – фаза колебания в момент времени t;

j0 – начальная фаза колебания.

Круговая частота , где Т – период колебаний: .

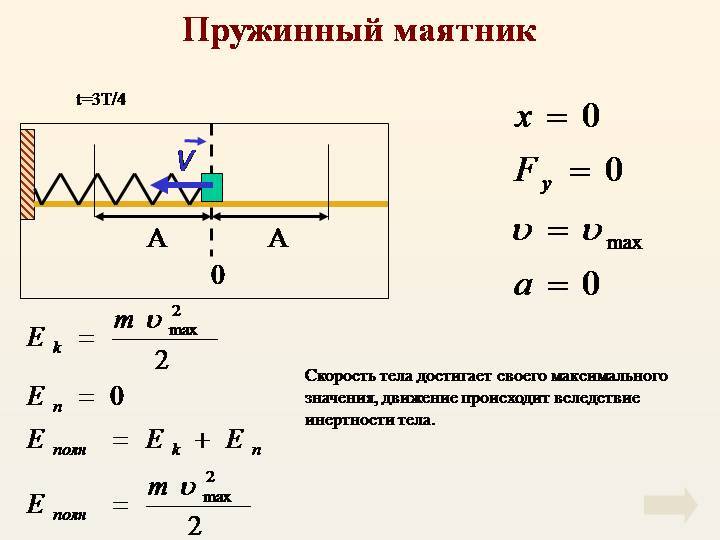
Кинетическая энергия колебаний пружинного маятника:

Потенциальная энергия колебаний пружинного маятника:

Полная энергия колебаний пружинного маятника:

,

откуда видно, что полная энергия свободных незатухающих гармонических колебаний пружинного маятника остается со временем постоянной.

Свободные затухающие гармонические колебания пружинного маятника (рис. 6). Для пружинного маятника массой т, совершающего колебания под действием упругой силы (Fx = – kx)с учетомсилы сопротивления , пропорциональной скорости движения груза (), второй закон Ньютона имеет вид:

,

где r – коэффициент сопротивления.

Обозначив и ( – коэффициент затухания), получим дифференциальное уравнение свободных затухающих гармонических колебаний пружинного маятника:

Решением этого дифференциального уравнения в случае малых затуханий

является функция x(t):

,

где – амплитуда затухающих колебаний в момент времени t;

– начальная амплитуда, т.е. амплитуда в момент времени t = 0,

– круговая (циклическая) частота:

Период затухающих гармонических колебаний пружинного маятника:

Рис. 6

Декремент затухания. Если A(t)и А(t+Т) – амплитуды двух последовательных колебаний (рис. 6), то отношение этих величин называется декрементом затухания .

Логарифм называется логарифмическим декрементом затухания :

Вопрос 16

Текст вопроса

BB2c18 В первой серии опытов по исследованию малых колебаний разных грузов на нити одинаковой длины использовался железный грузик, во второй – алюминиевый такого же объёма. Угол отклонения нити от вертикали в обоих исследованиях одинаковый.

Читать также: Диаметр сверла для мебельного шурупа

Как при переходе от первой серии опытов ко второй изменяется период колебаний, частота и максимальная кинетическая энергия груза?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Момент силы и момент импульса относительно оси

Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.

Момент импульса – величина, которая применяется для определения количества вращательного движения.

Среди особенностей подобного показателя можно отметить следующее:

1. Масса вращения. Объект может характеризоваться различной массой.
2. Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
3. Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.

Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.

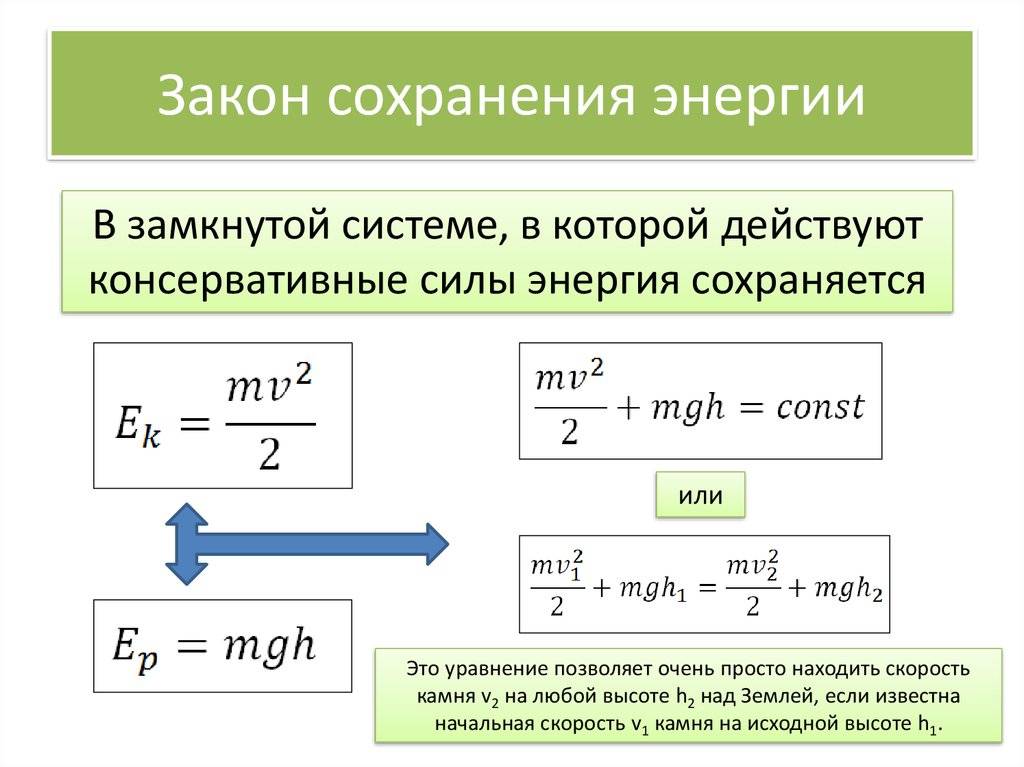
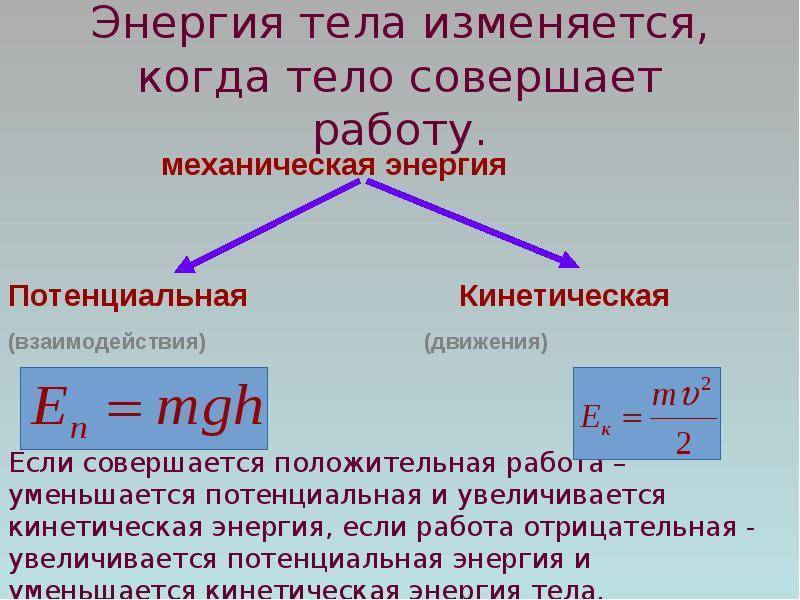
Закон сохранения энергии

В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.

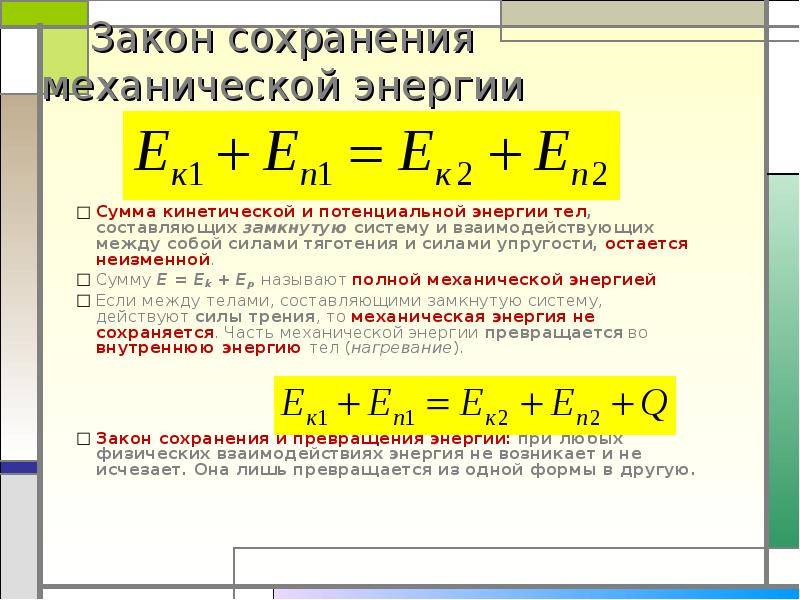
Закон сохранения энергии Полная механическая энергия замкнутой системы остается постоянной.

Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:

Закон сохранения энергии Еполн. мех. = Еп + Eк = const Еполн. мех. — полная механическая энергия системы Еп — потенциальная энергия Ек — кинетическая энергия const — постоянная величина

Задачка раз

Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?

Решение:

Должен выполняться закон сохранения энергии:

В начальный момент времени высота равна нулю, значит Е_п = 0. В этот же момент времени Е_к максимальна.

В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.

Это можно описать соотношением:

Е_п1 + Е_к1 = Е_п2 + Е_к2

0 + Е_к1 = Е_п2 + 0

Е_к1 = Е_п2

Разделим на массу левую и правую часть

Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.

Ответ: высота увеличится в 4 раза

Задачка два

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v, поднялось на максимальную высоту h. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?

Решение

По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Е_мех = Е_п = mgh.

Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Е_мех = mgh.

Ответ: Е_мех = mgh.

Задачка три

Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.

Решение:

Переведем массу из граммов в килограммы:

m = 100 г = 0,1 кг

У поверхности земли полная механическая энергия мяча равна его кинетической энергии:

Дж

На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:

Дж

м

Ответ: мяч имел скорость 2 м/с на высоте 1,6 м

Сила упругости в пружинном маятнике

Следует учитывать тот момент, что до деформирования пружины она находится в положении равновесия. Приложенная сила может приводить к ее растягиванию и сжиманию. Сила упругости в пружинном маятнике рассчитывается в соответствии с тем, как воздействует закон сохранения энергии. Согласно принятым нормам возникающая упругость пропорциональна смещению тела. В этом случае кинетическая энергия рассчитывается по формуле: F=-kx. В данном случае применяется коэффициент жесткости пружины.

Выделяют довольно большое количество особенностей воздействия силы упругости в пружинном маятнике. Среди особенностей отметим:

1. Максимальная сила упругости возникает на момент, когда тело находится на максимальном расстоянии от положения равновесия. При этом в подобном положении отмечается максимальное значение ускорение тела. Не следует забывать о том, что может проводится растягивание и сжатие пружины, оба варианта несколько отличается. При сжатии минимальная длина изделия ограничивается. Как правило, она имеет длину, равную диаметру витка умноженное на количество. Слишком большое усилие может стать причиной смещения витков, а также деформации проволоки. При растяжении есть момент удлинения, после которого происходит деформация. Сильное удлинение приводит к тому, что возникающей силы упругости недостаточно для возврата изделия в первоначальное состояние.
2. При сближении тела к месту равновесия происходит существенное уменьшение длины пружины. За счет этого наблюдается постоянное снижение показателя ускорения. Все это происходит за счет воздействия усилия упругости, которая связано с типом применяемого материала при изготовлении пружины и ее особенностями. Длина уменьшается за счет того, что расстояние между витками снижается. Особенностью можно назвать равномерное распределение витков, лишь только в случае дефектов есть вероятность нарушения подобного правила.
3. На момент достижения точки равновесия сила упругости снижается до нуля. Однако, скорость не снижается, так как тело движется по инерции. Точка равновесия характеризуется тем, что длина изделия в ней сохраняется на протяжении длительного периода при условии отсутствия внешнего деформирующего усилия. Точка равновесия определяется в случае построения схемы.
4. После достижения точки равновесия возникающая упругость начинает снижать скорость перемещения тела. Она действует в противоположном направлении. При этом возникает усилие, которое направлено в обратную сторону.
5. Дойдя крайней точки тело начинает двигаться в противоположную сторону. В зависимости от жесткости установленной пружины подобное действие будет повторятся неоднократно. Протяженность этого цикла зависит от самых различных моментов. Примером можно назвать массу тела, а также максимальное приложенное усилие для возникновения деформации. В некоторых случаях колебательные движения практически незаметны, но они все же возникают.

Приведенная выше информация указывает на то, что колебательные движения совершаются за счет воздействия упругости. Деформация происходит за счет приложенного усилия, которое может варьировать в достаточно большом диапазоне, все зависит от конкретного случая.

Кинетическая энергия

Движущееся тело характеризуется скалярной величиной (масса) и векторная величина (скорость). Если рассматривать реальное перемещение в пространстве, то можно записать уравнение для определения кинетической энергии:

здесь v – скорость движения тела, м/с.

Использование кинетического преобразования можно наблюдать при колке орехов.

Приподняв камень повыше, далекие предки создавали необходимый потенциал для тяжелого тела.

Приподняв камень на максимальную высоту, разрешают ему свободно падать.

Двигаясь с высоты h

, он набирает скорость

Поэтому в конце падения будет получена кинетическая энергия

Рассматривая входящие величины, можно увидеть, как происходит преобразование величин. В конце получается расчетная формула для определения потенциальной энергии.

Даже на уровне вывода зависимостей можно наблюдать выполнение закона сохранения энергии твердого тела.

Уравнение движения вращающегося тела

Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек

При этом отметим нижеприведенные особенности:

1. Прямая, которая соединяет две точки, выступает в качестве оси вращения.
2. Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
3. Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.

Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt

В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной

Пружинный маятник

Это устройство является простейшим примером свободных колебаний. В его состав входит кронштейн, пружина и груз. В качестве последнего может выступать любое физическое тело. Масса пружины по сравнению с грузом считается малой и при исследованиях не учитывается.

При изучении такой системы важной задачей является измерение периода движения тела, подвешенного к пружине. Определение понятию пружинного маятника, которое даётся в учебниках по физике довольно обобщённое

Считается, что это конструкция, в которой тело, имеющее массу m, подвешено на упругой пружине обладающей жёсткостью K. При этом из состояния равновесия систему может вывести упругая сила F = — k * x, где: x- расстояние от середины пружинного элемента до поверхности прикреплённого к нему груза.

Можно выделить два достаточных условия возникновения свободных колебаний:

• Во время отклонения тела от положения равновесия должна возникать возвращающая сила.
• Силы сопротивления (трения) должны быть малы по сравнению со стремящей вернуть энергией тело назад.

Суть изучения гармонических колебаний состоит в определении их частоты движения или периода. В пружинном маятнике, впрочем, как и в любой колебательной системе, параметры зависят от ряда характеристик. Из основных величин, описывающих процесс, можно выделить: массу груза и жёсткость. Поэтому задача и состоит в выяснении, как период зависит от этих двух параметров.

Во время экспериментов регулировать массу довольно легко. Для этого можно взять эталонные гири и, соединяя их, увеличивать вес. Жёсткость же пружины можно изменить, добавляя параллельно или последовательно к ней другое сжимающееся тело. Чтобы выяснить, как будет изменяться характеристика растягивающегося элемента, нужно знать, что же представляет собой параметр. Так, под жёсткостью тела понимают отношение силы упругости к удлинению: k0 = F / Δ L. Измеряется величина в ньютонах, делённых на метр (Н/м).

Исходя из правила, если соединить две пружины параллельно и деформировать их, то можно утверждать, что первый и второй элемент растянется на одинаковую длину ΔL. Значит, возникнет две одинаково направленных силы упругости. Отсюда равнодействующая будет равняться: K = 2F/ ΔL = 2k0. Для последовательного же соединения длина всей системы увеличится на 2 ΔL. Сила упругости будет равна F. Соответственно, жёсткость будет изменяться по формуле: K = F / 2ΔL = k0 / 2.

Зависимость периода

При проведении эксперимента можно исследовать пять различных комбинаций поведения груза на пружине — два варианта связаны с весом и три с жёсткостью. Чтобы выполнить опыт самостоятельно нужно будет взять вертикальный кронштейн, две одинаковые пружины и два равных по весу груза. Так как в реальности период будет довольно маленький, то для его измерения можно взять время, например, пятидесяти колебаний, а потом полученный результат разделить на это число. Подсчёт времени удобно выполнять с помощью секундомера.

Вычисленные результаты нужно занести в таблицу. Примерный порядок чисел должен получиться таким:

k m	m0	2m0
k0 / 2	0,68	0,93
k0	0,46	0,64
2k0	0.34	0,47

Эти данные можно проанализировать. Выводы будут следующими:

с ростом массы физического тела период цикличности увеличивается;
по мере увеличения жёсткости период колебаний уменьшается.

Приведённые утверждения, возможно, описать и количественно. Исходя из результатов, величины, стоящие в ячейке m0k0 и 2m02ko почти совпадают. С точки зрения физики, так и должно быть. Если взять грузик на пружине и измерить характеристику, а потом добавить к нему точно такую же систему, то период не поменяется. Это и можно наблюдать во время опыта. Значит, период движения зависит от того каким будет отношение массы к жёсткости.

По аналогии можно рассмотреть, как влияет жёсткость. Из эксперимента, видно, что если её увеличить дважды на одну и ту же величину, то она возрастёт в четыре раза, а значение обратное частоте уменьшится на это же число. Отсюда можно предположить, что период будет обратно пропорционален корню квадратному из жёсткости.

Объединив эти две гипотезы можно сделать заключение. Что период амплитуды колебаний груза на пружине будет прямо пропорционален корню квадратного из отношения массы к жёсткости: T = √(m / k). Проверить это утверждение можно по теории размерности. Подставив в формулу единицы измерения, получим: √(m / k) = √(кг / (Н/м)) = √(кг * м / Н). Учитывая, что ньютон — это отношение метра к секунде в квадрате или килограмму, умноженному на метр и делённому на секунду, размерное равенство примет вид: √(кг * м/Н) = √(c2 * м/м) = √с2 = с.

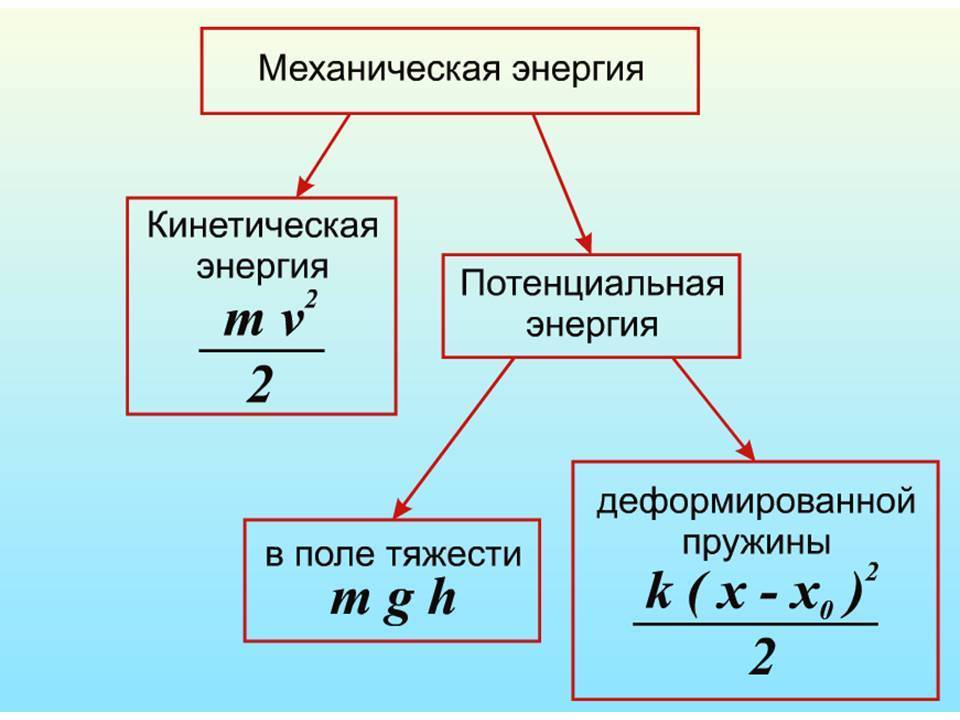
Механическая энергия

Кинетическая энергия тела

\(~E_k = \frac{m \cdot \upsilon^2}{2}\) , где E

k – кинетическая энергия тела (Дж);m – масса тела (кг);υ – скорость тела (м/с).

Теорема об изменении кинетической энергии

\(~A = \Delta E_k\) ,

где A

– механическая работа силы, действующей на тело (Дж); \(~\Delta E_k = \frac{m \cdot \upsilon^2}{2} — \frac{m \cdot \upsilon^2_0}{2}\) – изменение кинетической энергии тела (Дж);m – масса тела (кг);υ иυ 0 – конечная и начальная скорости тела (м/с).

Потенциальная энергия взаимодействия тела и Земли

\(~E_p = m \cdot g \cdot h\) , где E

p – потенциальная энергия тела (взаимодействия тела и Земли) (Дж);m – масса тела (кг);g – ускорение свободного падения, у поверхности Земли равна 9,8 м/с2 ≈ 10 м/с2;h – высота тела над нулевой высотой (м).

За нулевую высоту (уровень), по умолчанию, принято считать поверхность земли.

\(~A = -\Delta E_p\) , где A

– работа консервативных сил (силы тяжести) (Дж); ΔE p =mgh –mgh 0 – изменение потенциальной энергии тела (взаимодействия тела и Земли) (Дж);m – масса тела (кг);g – ускорение свободного падения, у поверхности Земли равна 9,8 м/с2 ≈ 10 м/с2;h иh 0 – конечная и начальная высоты тела над нулевой высотой (м).

За нулевую высоту (уровень), по умолчанию, принято считать поверхность земли.

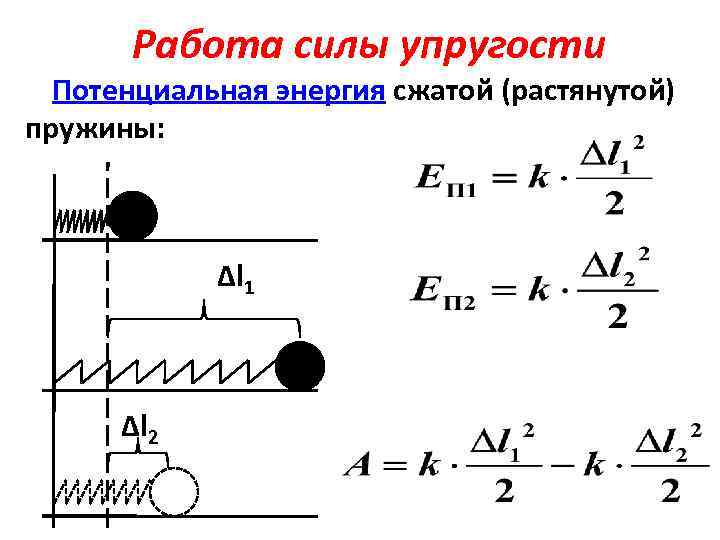
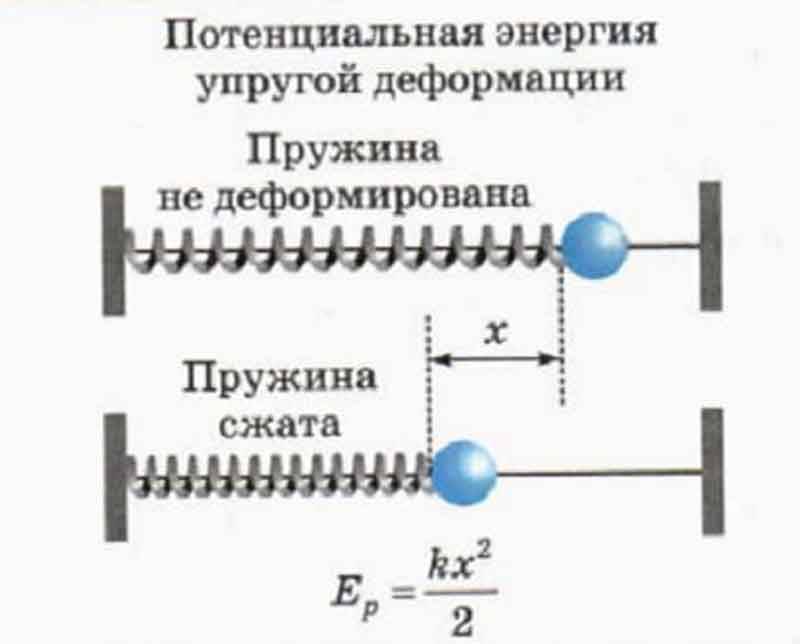
Потенциальная энергия деформированной пружины

\(~E_p = \frac{k \cdot \Delta l^2}{2}\) , где E

p – потенциальная энергия деформированной пружины (Дж);k – коэффициент жесткости пружины (Н/м); Δl = |l –l 0| – абсолютное удлинение (удлинение) пружины (м);l иl 0 – конечная и начальная длины пружины (м). \(~A = -\Delta E_p\) , где A

– работа консервативных сил (силы упругости) (Дж); \(~\Delta E_p = \frac{k \cdot \Delta l^2}{2} — \frac{k \cdot \Delta l^2_0}{2}\) – изменение потенциальной энергии пружины (Дж);k – коэффициент жесткости пружины (Н/м); Δl и Δl 0 – конечное и начальное абсолютные удлинения (конечное и начальное удлинения) пружины (м).

По умолчанию считаем, что пружина вначале не деформирована, т.е. Δl 0 = 0.

Физика

3.4. Механическая энергия

3.4.2. Потенциальная энергия

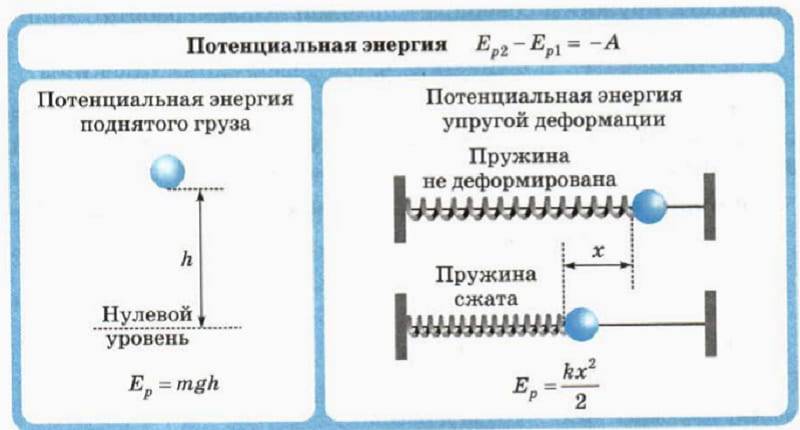
Потенциальная энергия — это механическая энергия системы тел, определяемая их (или частей одного тела) взаимным расположением.

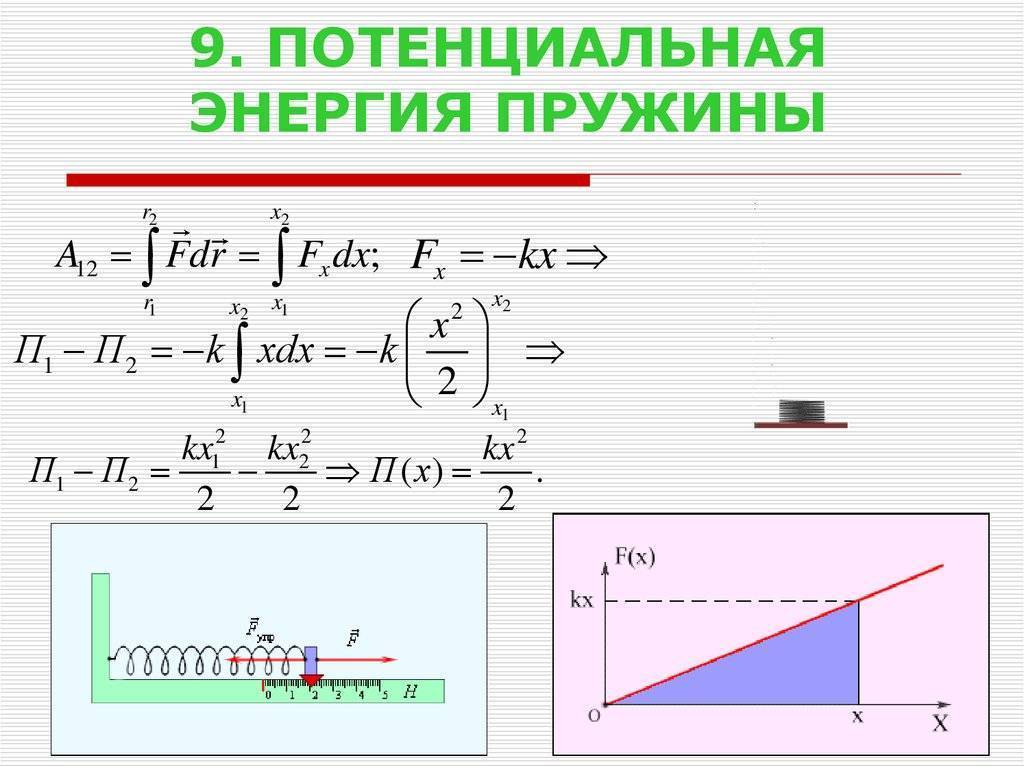
Потенциальная энергия деформированной пружины

Деформированная пружина (сжатая или растянутая) (рис. 3.7) обладает потенци­альной энергией, которая определяется формулой

W p = k ( Δ l ) 2 2 ,

где k — коэффициент жесткости (упругости) пружины; ∆l — величина абсолютной деформации пружины (удлинения или сжатия).

Рис. 3.7

Потенциальная энергия недеформированной пружины равна нулю.

Следует отметить, что потенциальная энергия деформированной пружины всегда является положительной величиной.

В Международной системе единиц потенциальная энергия деформированной пружины измеряется в джоулях (1 Дж).

Потенциальная энергия взаимодействия тела и Земли

Тело, расположенное на расстоянии h над поверхностью Земли (или под ее поверхностью), обладает потенциальной энергией, которая определяется формулой

Wp = mgh + C,

где m — масса тела; g — модуль ускорения свободного падения.

Выбор константы C является условным и зависит от конкретной задачи; часто указанную константу выбирают таким образом, чтобы на поверхности планеты потенциальная энергия взаимодействия тела и планеты обращалась в ноль.

Следует отметить, что потенциальная энергия взаимодействия тела и Земли может быть как положительной, так и отрицательной величиной.

В Международной системе единиц потенциальная энергия тела, поднятого на некоторую высоту относительно поверхности Земли, измеряется в джоулях (1 Дж).

Пример 26. Две пружины с одинаковыми коэффициентами жесткости по 1,0 кН/м соединили последовательно. Составную пружину растянули на 10 см. Во сколько раз увеличится потенциальная энергия деформации, если эти же пружины соединить параллельно, а величину деформации системы оставить прежней? Рассчитать потенциальную энергию пружин при последовательном и параллельном соединении, считая деформацию составной пружины одинаковой и равной 10 см.

Решение. Потенциальная энергия составной пружины определяется формулой

W p = k общ ( Δ l ) 2 2 ,

где kобщ — общий коэффициент жесткости составной пружины; ∆l — величина деформации пружины.

Коэффициент жесткости составной пружины определяется по-разному:

для N одинаковых пружин, соединенных последовательно,

k общ 1 = k 0 N ;

для N одинаковых пружин, соединенных параллельно,

kобщ2 = Nk0,

где k0 — коэффициент жесткости одной пружины; N = 2 — количество соединенных пружин.

Потенциальная энергия составной пружины вычисляется по формулам:

для N одинаковых пружин, соединенных последовательно,

W p 1 = k общ 1 ( Δ l ) 2 2 = k 0 ( Δ l ) 2 2 N ;

для N одинаковых пружин, соединенных параллельно,

W p 2 = k общ 2 ( Δ l ) 2 2 = N k 0 ( Δ l ) 2 2 .

Отношение потенциальных энергий

W p 1 W p 2 = k 0 ( Δ l ) 2 2 N 2 N k 0 ( Δ l ) 2 = 1 N 2

определяется только количеством пружин и не зависит от деформации составной пружины.

Рассчитаем потенциальную энергию составной пружины, состоящей из двух одинаковых пружин,

соединенных последовательно:

W p 1 = k 0 ( Δ l ) 2 2 N = 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 ⋅ 2 = 2,5 Дж;

соединенных параллельно:

W p 2 = N k 0 ( Δ l ) 2 2 = 2 ⋅ 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 = 10 Дж.

Отношение указанных потенциальных энергий равно

W p 1 W p 2 = 1 N 2 = 1 2 2 = 4 .

Следовательно, при одинаковой деформации потенциальная энергия пружины, составленной из двух одинаковых параллельно соединенных пружин, в 4 раза больше потенциальной энергии пружины, составленной из двух одинаковых последовательно соединенных пружин.

Пример 27. Какой энергией обладает тело массой 500 г на вершине горы относительно дна озера, находящегося у подножия горы? Высота горы составляет 1,50 км, а глубина озера 250 м.

Решение. Потенциальная энергия тела, поднятого на некоторую высоту, определяется формулой

Wp = mgh,

где m — масса тела; g — модуль ускорения свободного падения; h — высота, на которую поднято тело над определенным уровнем, характеризуемым нулевым значением потенциальной энергии.

Выберем нулевой уровень потенциальной энергии (Wp = 0) на дне озера так, как показано на рисунке.

Тогда высота, на которую поднято тело над указанным уровнем, является суммой:

h = h2 + h2,

где h2 = 1,50 км — высота горы; h2 = 250 м — глубина озера.

Потенциальная энергия тела относительно дна озера определяется выражением

Wp = mg(h2 + h2).

Расчет дает значение:

W p = 500 ⋅ 10 − 3 ⋅ 10 ⋅ ( 1,50 + 0,25 ) ⋅ 10 3 = 8,75 ⋅ 10 3 Дж = 8,75 кДж.