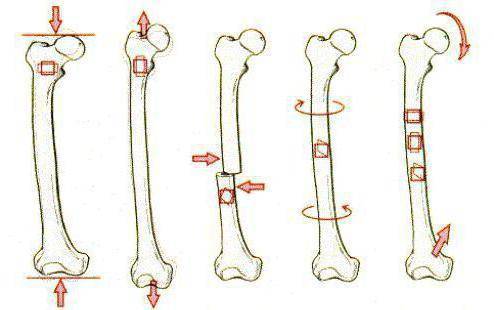
Расчёты на прочность при изгибе
Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом. Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта
Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.
Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.
Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:
- дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
- способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
- семейство принятых гипотез;
- разработанные правила построения графических изображений (построение эпюр).
Расчёт параметров производится в три этапа:
- при проверочном расчёте (вычисляют величину максимального напряжения);
- на этапе проектирования (производится выбор толщины и параметров сечения бруса);
- во время вычисления допустимой нагрузки.
Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.
Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей. При чистом изгибе эпюры имеют следующие особенности:
- на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
- на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
- в точке появления приложенного момента, скачок равен величине этого параметра;
- на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
- в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).
На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:
- расчёт производят с учётом нормальных напряжений;
- в качестве основного предположения принимают гипотезу о плоских сечениях;
- продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
- деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
- для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
- физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
- процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).
Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.
Предел прочности
Определение 9
Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.
В точке e материал разрушается.
Определение 10
Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.
Определение 11
Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.
Деформация сдвига имеет аналогичные закономерности и свойства. Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела. Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела). Для малых деформаций действует следующая формула:
∆xl=1GFS
Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Нм2, G=,42·1011 Нм2.
Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен. При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела
При малых деформациях
Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях
При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях
∆VV=1Bp
Буквой B обозначен коэффициент пропорциональности, называемый модулем всестороннего сжатия. Такому сжатию можно подвергнуть не только твердое тело, но и жидкость и газ. Так, у воды B=2,2·109 Нм2, у стали B=1,6·1011Нм2. В Тихом океане на глубине 4 км давление составляет 4·107 Нм2, а относительно изменения объема воды 1,8 %. Для твердого тела, изготовленного из стали, значение этого параметра равно ,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно. Газы могут сжиматься еще лучше, чем тела и жидкости.
От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.
Всё ещё сложно? Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Напряжение при сдвиге
Воздействие внешней силы на грань приводит к возникновению в изделии изменения формы. Все напряжения делятся на две категории: нормальные и касательные. Нормальными считаются внутренние напряжения, возникающие в различных слоях изделия, подверженного деформации.
Напряжения и деформации при сдвиге описываются с применением аналитических выражений и графических изображений. Общее состояние описывается пространственным (трёхкоординатным) напряжением. Если в конкретном случае можно выявить сечения, в которых оба вида напряжений равны нулю, можно перейти к более простым моделям описания этого процесса. Ими являются двухкоординатное (плоское) напряжённое состояние или линейное. Две последних модели являются частными случаями трёхкоординатного напряжённого состояния.

Касательные напряжения являются мерой скольжения одного поперечного слоя относительно другого. В изменениях на поверхности каждого слоя возникают только касательные напряжения. Для оценки полной картины деформации используют следующие теоретические положения:
- закон парности касательных напряжений;
- вычисление экстремальных нормальных напряжений;
- определение всех тангенциальных напряжений.
Оценка их всех при деформации смещения позволят оценить прочность конструкции.
Определение[ | ]
Элемент g
группыG называетсяэлементом кручения , если он имеет конечный порядок, то есть существует натуральноеn , такое чтоgn =e , гдеe обозначат нейтральный элемент группы. Группа называется периодической (илигруппой кручения ), если все её элементы являются элементами кручения, игруппой без кручения , если единственный элемент кручения — нейтральный. Известно, что любая абелева группа является модулем над кольцом целых чисел; в частности, определение элемента кручения для неё можно переформулировать так: существует ненулевое целое число, такое что умножение на это число переводит данный элемент в ноль. Это мотивирует следующее определение:
Элемент m
модуляM над кольцомR называетсяэлементом кручения , если существует ненулевой регулярный элементr кольцаR (то есть элемент, не являющийся левым или правым делителем нуля), аннулирующийm , то есть такой, чтоrm = 0. В случае работы с целостным кольцом предположение регулярности можно отбросить. Аналогичным образом определяются модуль кручения и модуль без кручения. В случае, если кольцоR коммутативно, можество всех элементов кручения модуляM образует подмодуль, называемыйподмодулем кручения (в частности, для модуля надZ он называется подгруппой кручения).
Более общо, пусть M
— модуль над кольцомR иS — мультипликативно замкнутая система кольца. Элементm модуляM называется элементомS-кручения , если существует элемент мультипликативной системы, аннулирующийm . В частности, множество регулярных элементов кольца является наибольшей мультипликативной системой.
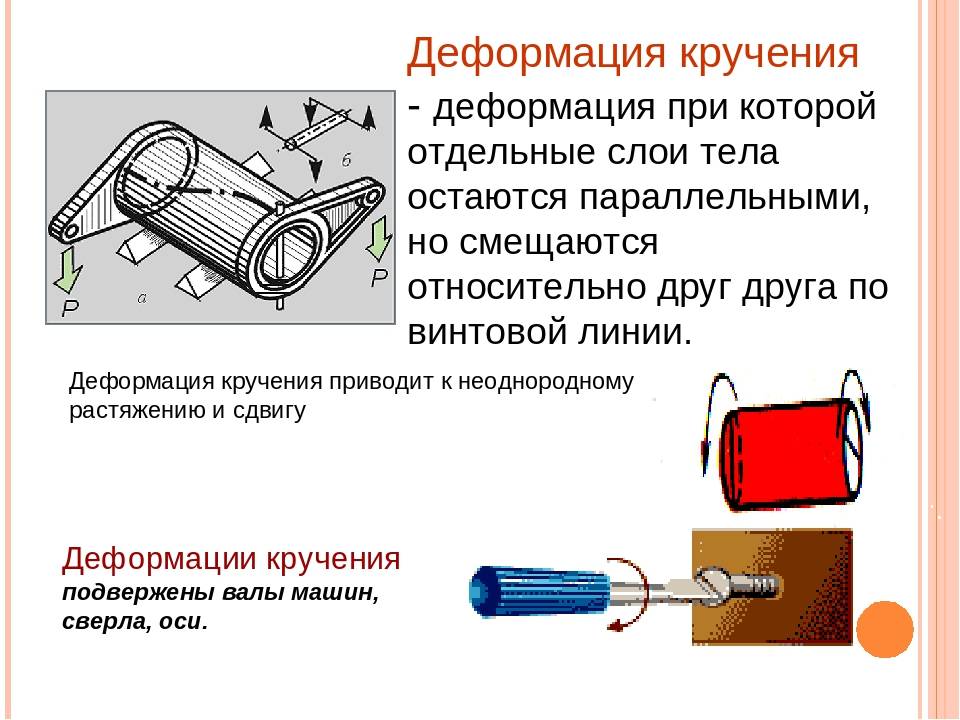
Деформация кручения
Напряжения и деформации при кручении
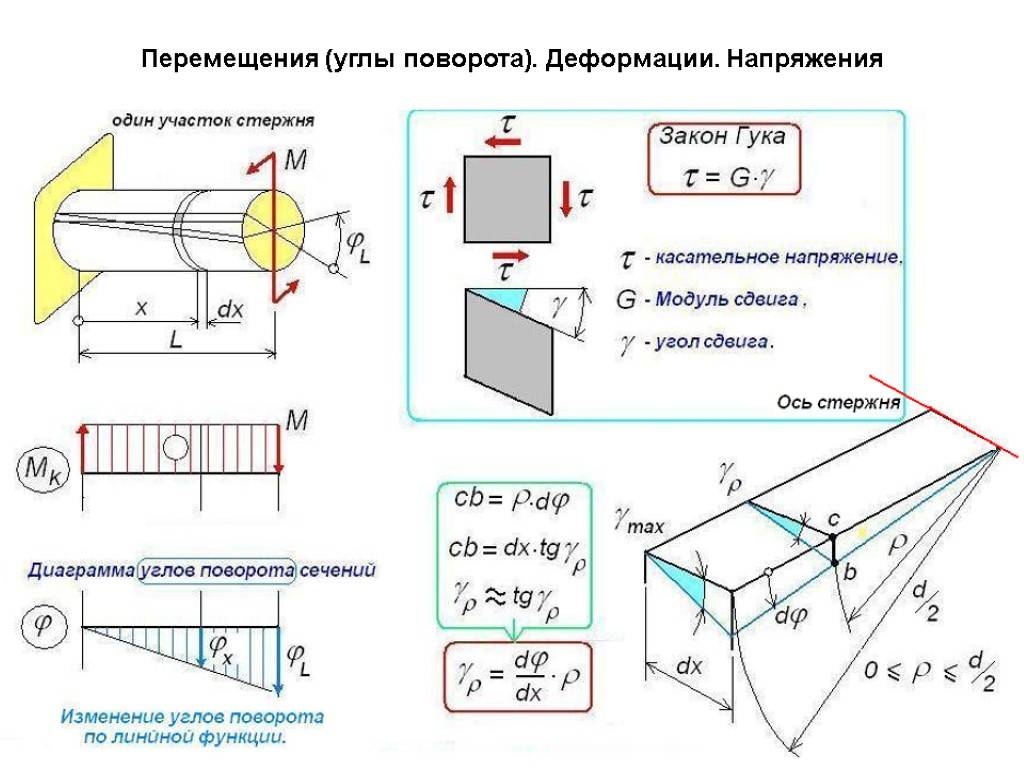
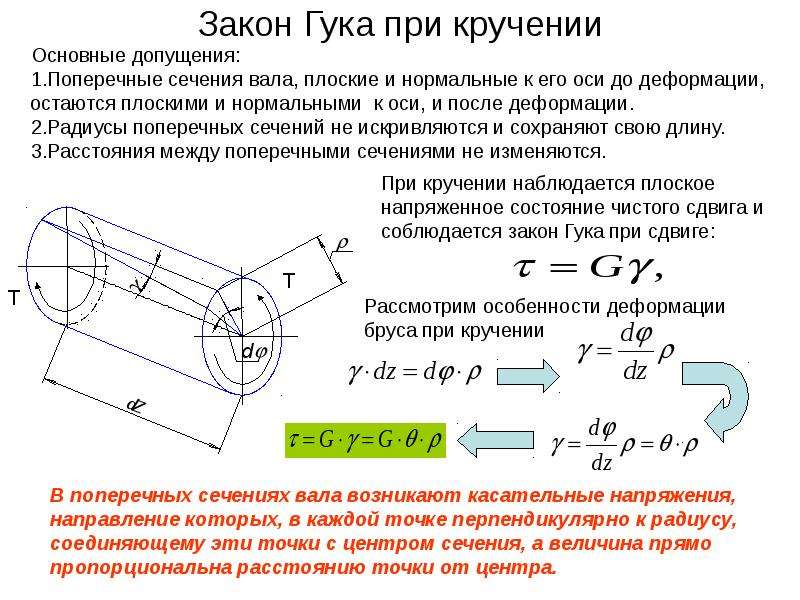
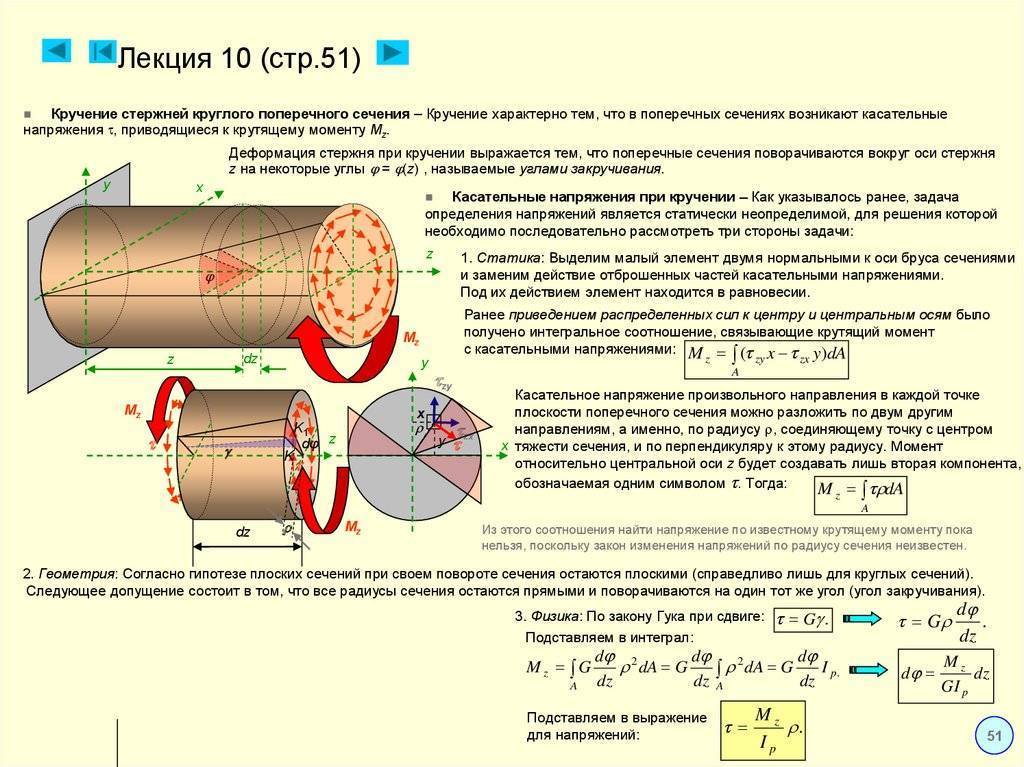
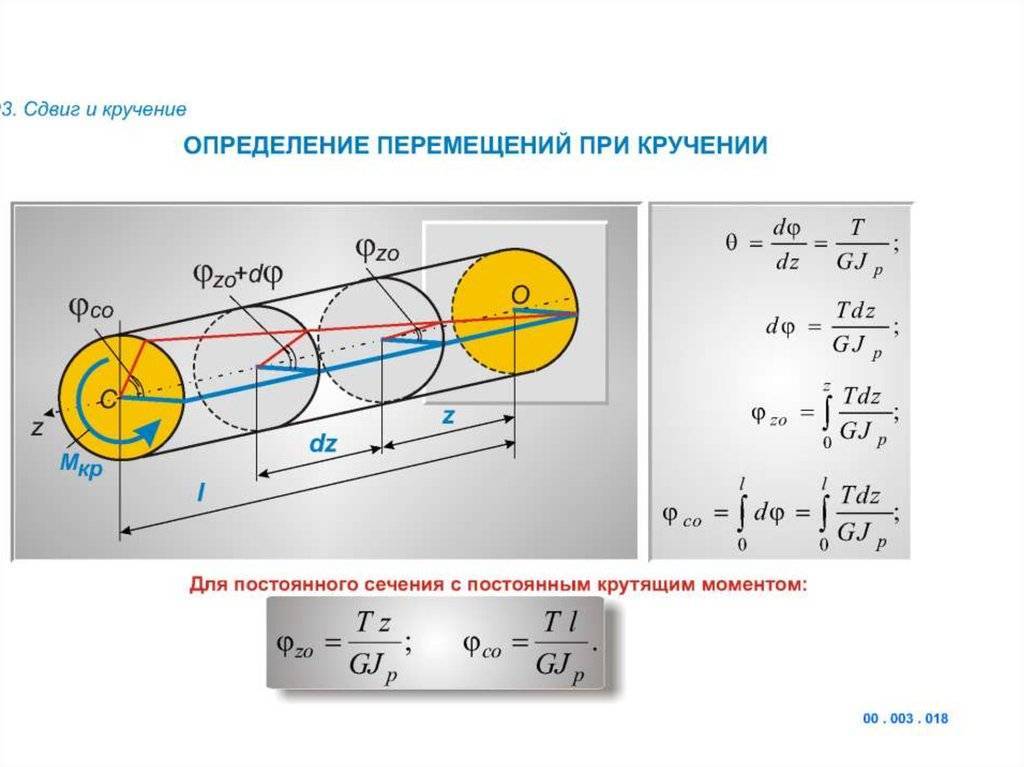
Исследование отдельных участков и слоев цилиндрического бруса, нагруженного скручивающим (вращающим) моментом, дает основание полагать, что в поперечных сечениях этого бруса нормальные напряжения (направленные вдоль оси) отсутствуют, а возникают только касательные напряжения, модули которых расположены в плоскости исследуемого сечения. Этот вывод опирается и на гипотезу о не надавливании волокон, предполагающую, что если брус представить в виде многочисленных цилиндрических продольных волокон, то при деформациях разного рода эти волокна не оказывают друг на друга силового воздействия (не давят друг на друга). Как показали многочисленные опыты и исследования, эта гипотеза справедлива в определенном интервале деформаций, и погрешностями в расчетах, связанными с ее применением, можно пренебречь.
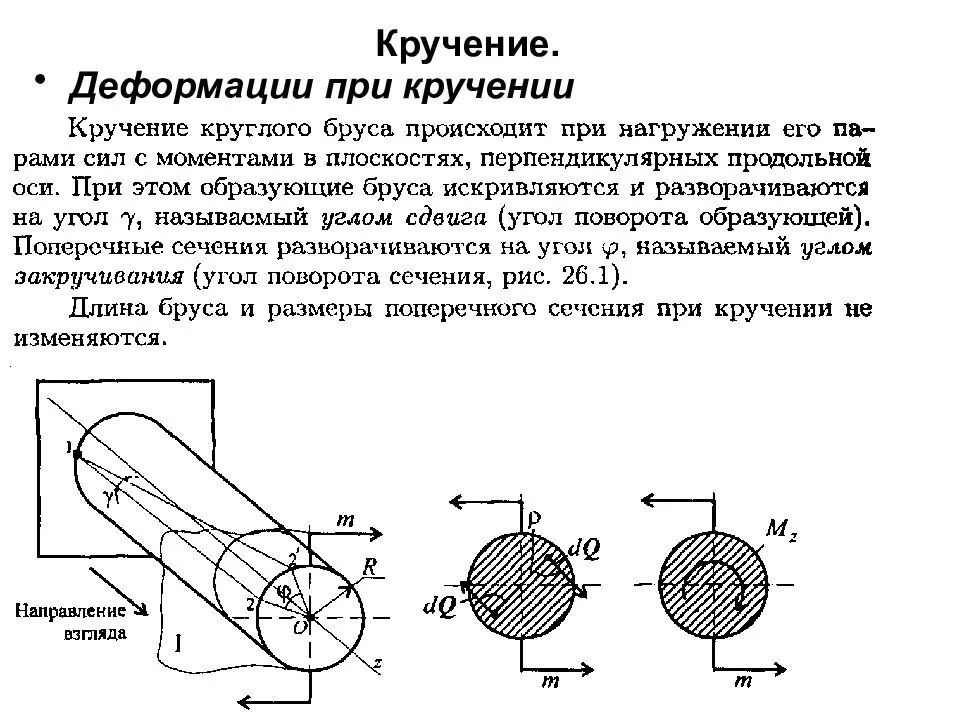
На рис. 1 видно, что абсолютный сдвиг сечения волокна а равен дуге аа1 , а сечения волокна b — дуге bb1 . Этот сдвиг (т. е. длины дуг) можно определить, зная угол φ закручивания исследуемого сечения относительно центральной оси: дуга аа1 = rφ ; дуга bb1 = Rφ , где: r — расстояние от волокна а до оси кручения, R — радиус сечения круглого бруса, φ — полный угол закручивания бруса.
Так как радиусы сечений при кручении бруса остаются прямыми (принятое предположение), то величина абсолютного сдвига сечения волокон прямо пропорциональна их расстоянию от оси кручения, т. е. чем дальше от оси расположено продольное волокно, тем сильнее сдвинется его сечение относительно центральной оси.
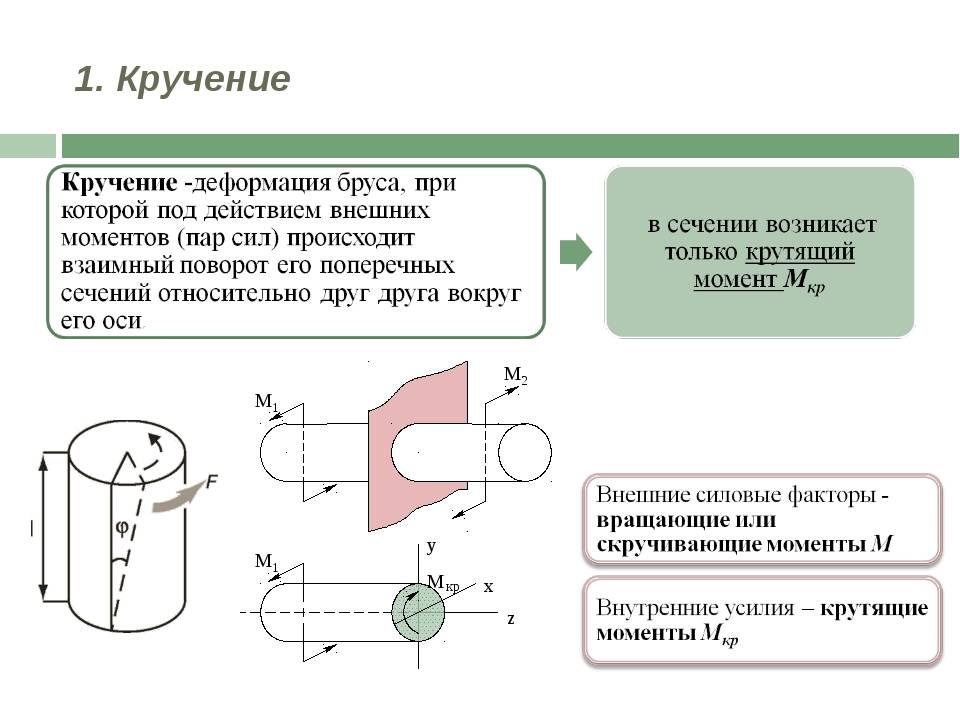
Кручение
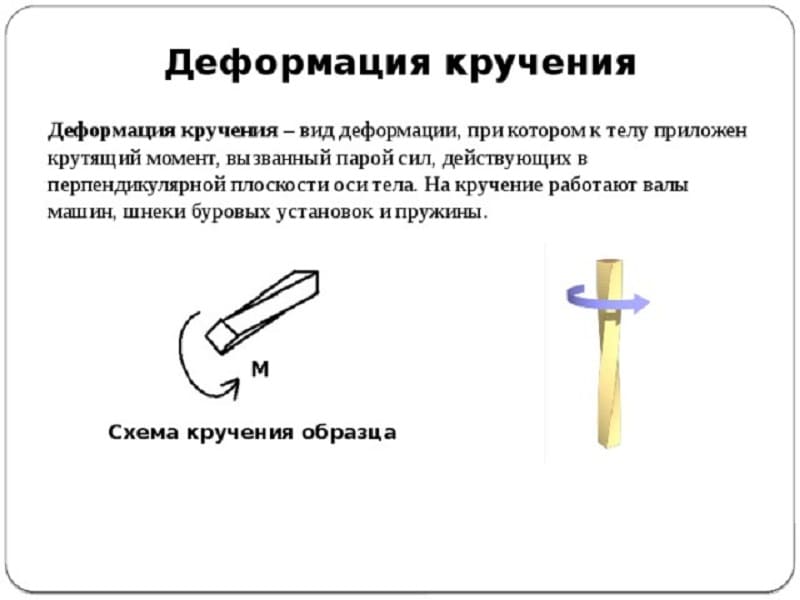
Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.
Деформацию кручения можно наблюдать, если на стержень, один конец которого закреплен, действует пара сил, лежащих в плоскости, перпендикулярной оси стержня. При кручении отдельные слои тела остаются параллельными, но поворачиваются друг относительно друга на некоторый угол. Деформация кручения представляет собой неравномерный сдвиг. Деформации кручения возникают при завинчивании гаек, при работе валов машин.
Пример деформации кручения цилиндрического стержня
Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ – угол кручения (рис. 1; 2).
Рис. 1.
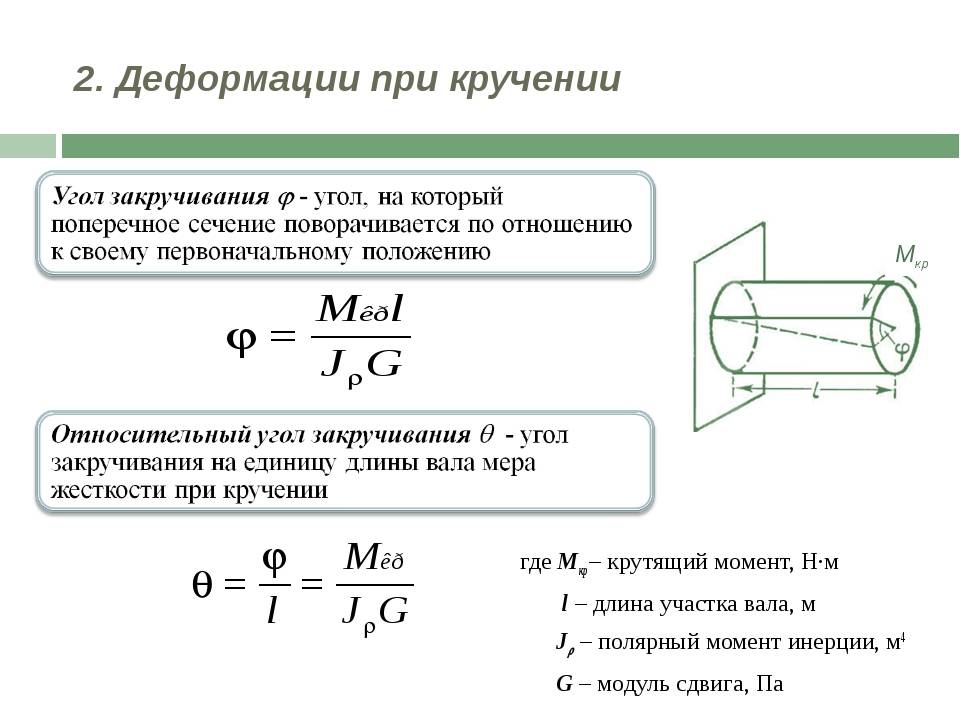
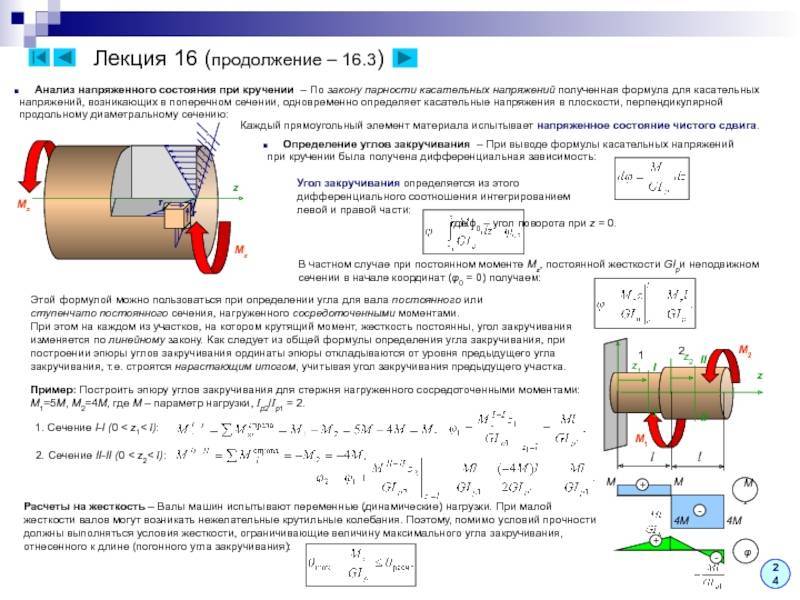
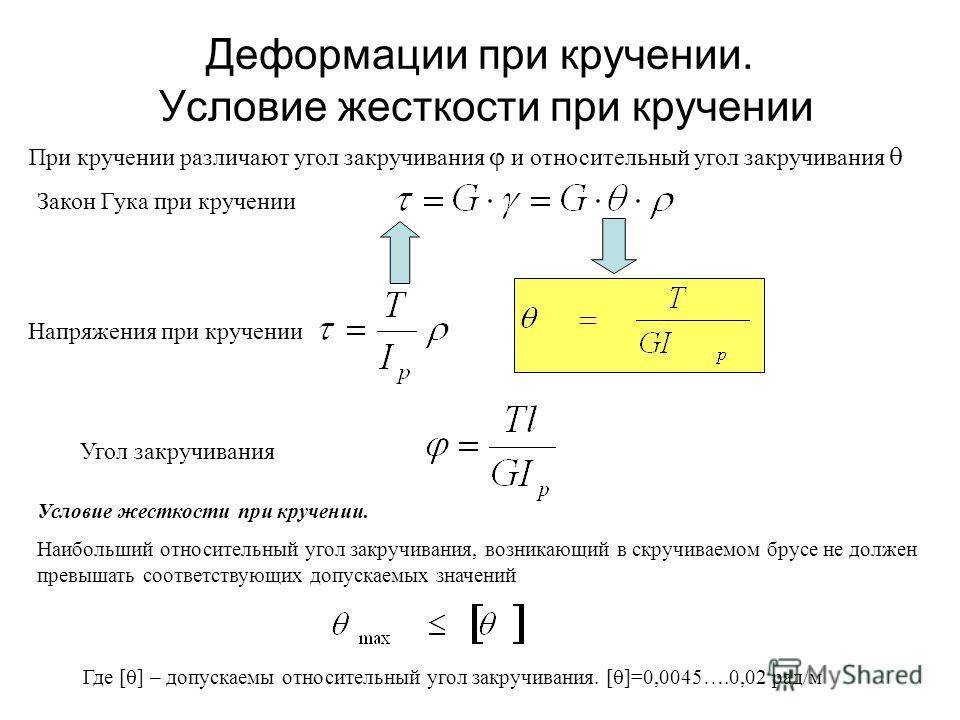
Отношение угла закручивания φ к длине называют относительным углом закручивания
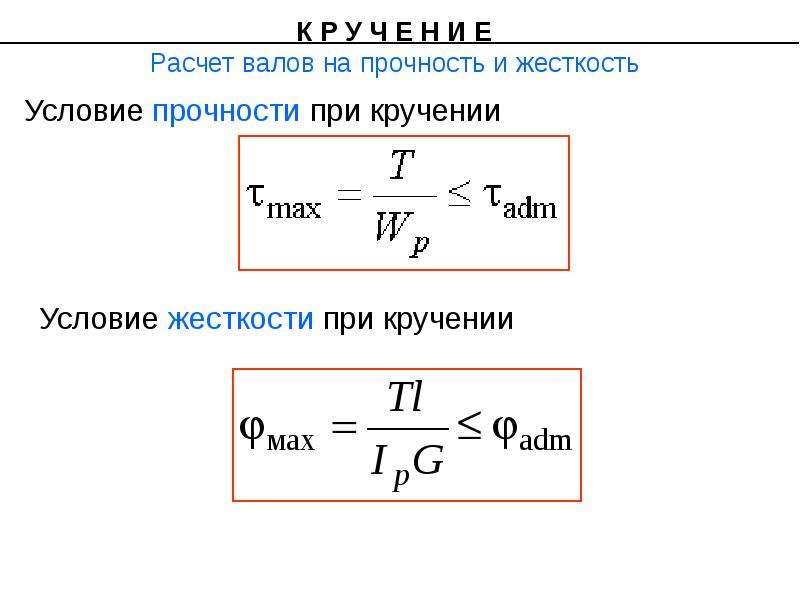
Закон Гука для малых деформаций кручения выражается формулой
M = Gкр.j
где Gкр.– модуль кручения.
Модуль кручения , помимо материала, зависит также от формы и размеров тела.
Представьте, перед вами цилиндр (или проволока). Если вы начнёте его (её) верхний конец поворачивать вдоль оси, закрепив нижний конец, то при повороте верхней грани на один радиан вы прикладываете вращающий момент, в точности равный модулю кручения (рис.1; 2). Это и есть его определение.
Модуль кручения Gкр показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.
Рис. 2.
Деформация кручения является частным случаем деформации сдвига.
Сдвиг
Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 3).
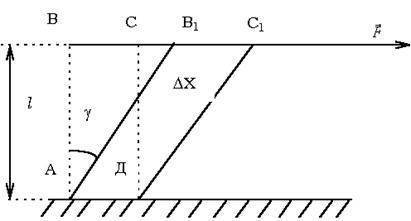
Рис. 3.
Деформация сдвига возникает под действием сил, приложенных к двум противоположным граням тела так, как показано на рисунках 3; 4. Эти силы вызывают смещение слоев тела, параллельных направлению сил. Расстояние между слоями не изменяется. Любой прямоугольный параллелепипед, мысленно выделенный в теле, превращается в наклонный.
Рис. 4.
Мерой деформации сдвига является угол сдвига γ — угол наклона вертикальных граней (рис. 5).
Рис. 5.
Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно.
Так как угол мал, формулу можно записать в виде:
где СС1 = D X — абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.
По закону Гука относительный сдвиг γ пропорционален касательному напряжению τ = F/S, где S — площадь поверхности грани ВС, т.е.
τ = F / S = Gg
где G — модуль сдвига.
Закон Гука для малой деформации сдвига выражается формулой:
Коэффициент G, зависящий от материала тела, называется модулем сдвига и характеризует упругие свойства тела при деформации сдвига. Например, для стального образца G = 76 ГПа.
Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).
Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. Сдвиг при больших углах приводит к разрушению тела — срезу. Срез происходит при работе ножниц, пилы и др.
Обратите внимание на принципиальное отличие модуля кручения от модуля сдвига, который зависит только от материала. Модуль кручения зависит не только от материала, но ещё и от диаметра и от длины цилиндра

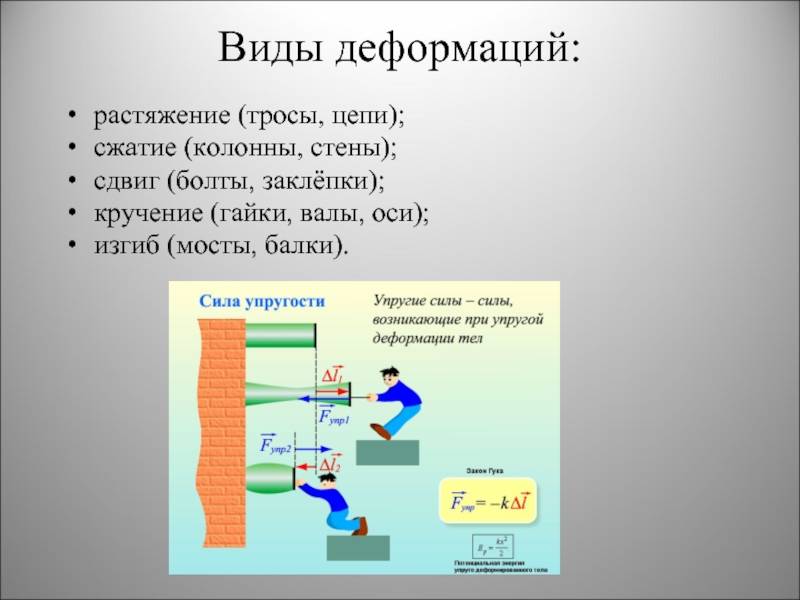
Сжатие и растяжение
Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.
Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.
Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.